基于Deform的椭圆筒形件旋压成形数值模拟

卢　璐

（山东科技大学机械电子工程学院，青岛 266000）

基于Deform的椭圆筒形件旋压成形数值模拟

卢璐

（山东科技大学机械电子工程学院，青岛 266000）

应用Deform 3D软件建立单旋轮椭圆筒形弹塑性有限元模型，通过设置旋轮绕旋轮轴自转、绕芯模主轴公转和沿芯模主轴方向偏移的运动，合成了椭圆筒形件运动轨迹。采用Dynaform软件反求毛坯尺寸，通过有限元模拟，获得了椭圆筒形件旋压过程中应力应变的分布规律，分析了毛坯形状对成形过程的影响。结果表明：旋压对已加工区的影响很小，并不易在后面即将加工的区域产生材料的堆积，最大等效应力变化不大；椭圆长径过渡到椭圆短径的区域内周向形状不均匀最显著，该区域内等效应变大；椭圆筒形件的旋压在实际生产过程中可以采用Dynaform反求出的毛坯为基础，根据具体情况进行修改和完善。

椭圆筒形件Deform等效应力应变毛坯形状

引言

旋压作为一种先进的无切削加工工艺，是塑性加工的一个重要分支。与传统金属加工技术相比，旋压是一种快速、经济的成形回转体零件的方法，具有可产生大塑性变形、变形力小、节约原材料、产品强度高等特点，适合加工多种金属材料。可旋压加工零件几何形状日益复杂，旋压成形技术已经突破传统的用于加工薄壁空心回转体零件的局限。已有不少学者对非轴对称类零件和非圆截面空心件的旋压成形技术进行了初步的探索研究，部分研究成果已经投入到成产实践中。日本SPINDLE公司于1999年研制出世界上第一台可生产偏心及倾斜类零件的数控旋压机床，并用于生产汽车的排气歧管和消音器［1］。德国THATE GmbH公司开发了一种针对旋压成形非圆形件的数控技术，并且尝试用数控旋压技术来生产椭圆形零件。美国MJC工程技术有限公司已经开发了一台全数控旋压机床，可加工从4570mm到150mm变径差的非圆形截面零件。国内，华南理工大学夏琴香研制的非轴对称零件旋压成形技术及设备，可完整加工各部分轴线相互平行或成一定夹角的偏心、倾斜类三维非轴对称薄壁空心零件［2］。本研究使用有限元分析软件Deform，对单旋轮椭圆筒形件旋压成形过程进行有限元模拟，研讨毛坯形状对成形过程的影响。

1　椭圆筒形件旋压成形有限元模型

1.1几何模型与工艺参数

该椭圆筒形件的初始毛坯由 Dynaform的反求功能获得，采用的旋压成形过程均为单旋轮一道次旋压成形，椭圆筒形件的初始毛坯尺寸为长径20.53mm、短径18.32mm的椭圆，厚度为1mm，旋轮直径为20mm，旋压成形几何模型示意图如图1所示。

工件由芯模和顶块夹紧，旋轮旋转且根据所需的轨迹进给并挤压坯料，使坯料产生连续的局部塑性变形，最终获得所需的椭圆筒形工件。旋压工艺参数如表1所示。

1.2有限元模型的轨迹设计

实际生产中，工件由顶块和芯模夹紧并高速转动。而在有限元模拟过程中，芯模每自转一步，软件都要重新计算模型的位置，重复的存储、读取动态数据，造成数据计算量巨大。因此，采用旋轮公转代替芯模自转的方法，可减少位置更新模型的数量，显著节省数据存储和计算量。旋压模拟过程中，通过设置旋轮绕旋轮轴自转的速度、绕芯模主轴公转的速度和沿芯模径向进给运动的速度，可以合成旋轮的椭圆形运动轨迹［3-6］。

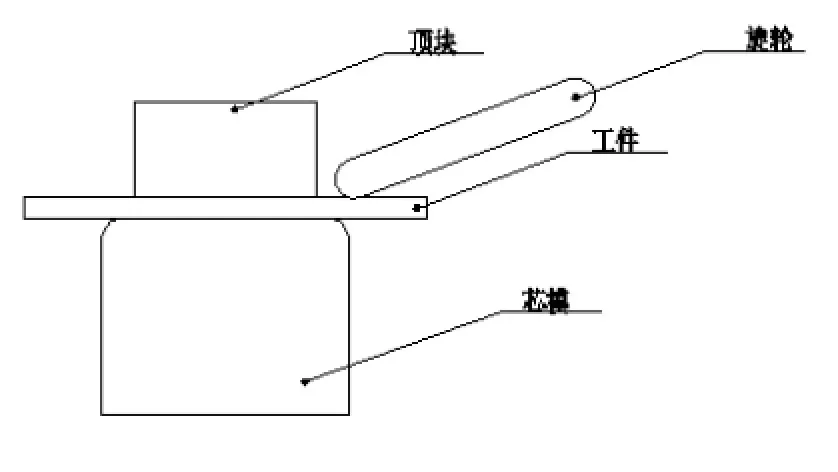
图1　几何模型

表1　旋压工艺参数

（1）旋轮公转。模拟中，将芯模和顶块设置为不旋转，旋轮设置为公转。其中，旋轮公转角速度与芯模自转角速度相等。旋轮公转角速度与主轴转速关系如式（1）所示。

式中，ω为旋轮公转角速度，n为主轴转速。

（2）旋轮自转。为保证模拟中旋轮与工件不发生打滑，要求旋轮与工件在接触点处时刻保持线速度相等。垂直于主轴方向上芯模的投影如图2所示。当转速恒定时，旋轮从长轴端点A运动到短轴端点S，旋轮与工件接触点线速度由最大值变为最小值。文中采用拟合方法，将A点至S点椭圆弧段划分为若干份，每一点对应一个线速度，以此求出旋轮接触该点时的自转角速度。离散的点数目越多，模拟中的运动轨迹与实际愈接近。考虑精度与计算效率的综合因素，本文将弧段划分为18份，并根据旋轮公转速度，做出旋轮自转角速度随时间变化曲线图，如图3所示。

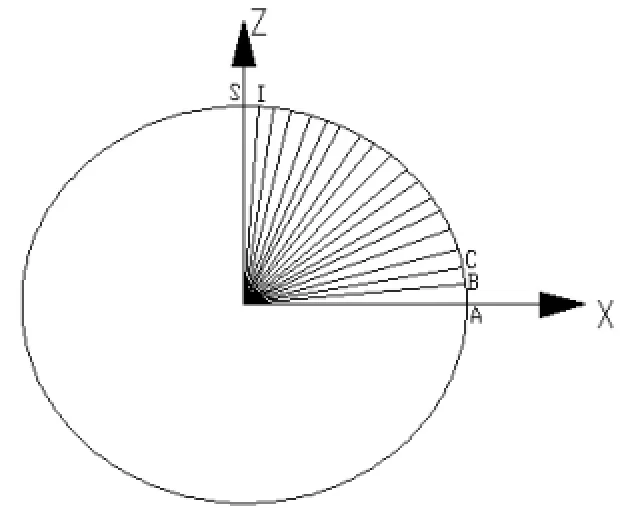
图2　Y方向芯模投影

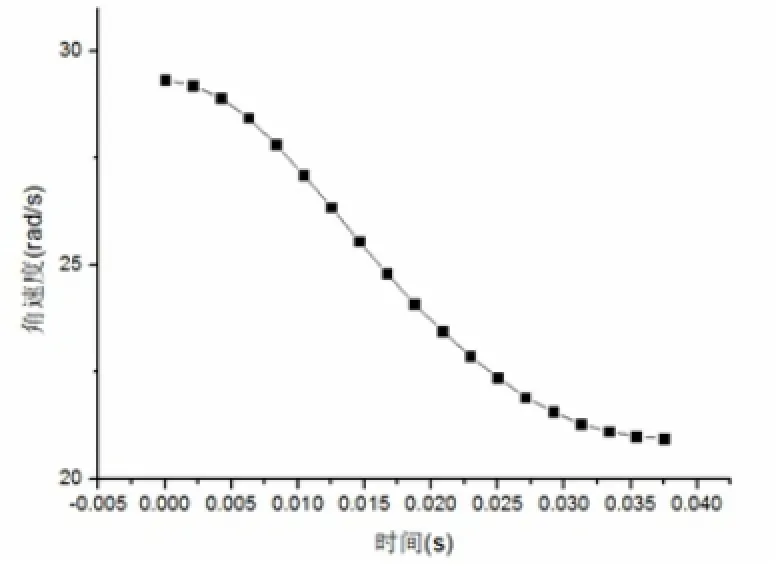
图3　旋轮自转速度与时间曲线图

（3）旋轮沿主轴偏移的运动。旋轮的公转轨迹为圆形，与旋轮沿主轴偏移的运动合成后为椭圆，在Deform中对如图2所示X方向进行运动设置，其中偏移速度如式（2）所示，旋轮偏移速度随时间变化曲线图，如图4所示。

式中，V偏为旋轮偏移速度，ROB为 B点到主轴的距离，ROA为A点到主轴的距离，T为芯模每转1/72圈所用的时间。

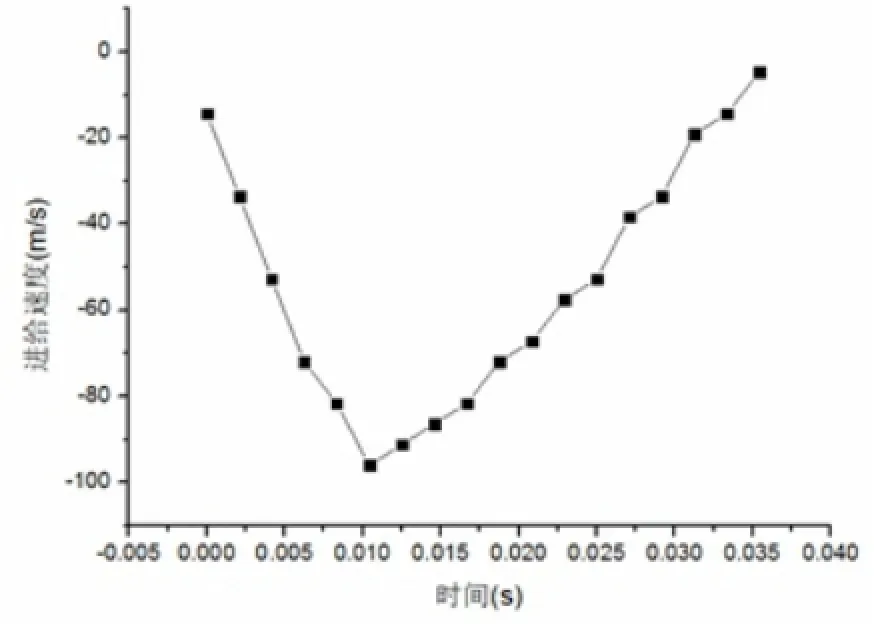
图4　偏移速度与时间曲线

1.3有限元模型的本构方程

本文建立的有限元模型为弹塑性有限元模型，工件材料为AL-1100，其本构方程如公式（3）所示。

式中，c为强度系数；n为硬化指数，0＜n＜1，其在Deform中应力应变曲线如图5所示。

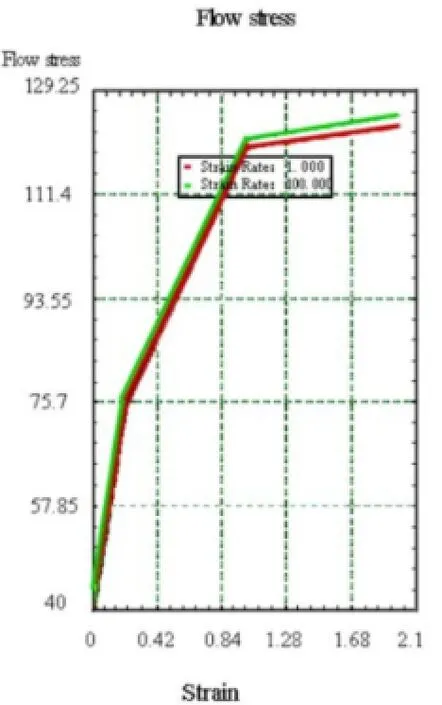
图5　AL-1100的应力应变曲线

2　应力应变分析

Dedorm软件的网格主要以四面体单元为主。实体划分网格时，四面体网格的单元属性将自动转换到实体上。网格数设置为130000，使工件在成形过程中减少网格发生畸变的数量，避免软件的自动重划分网格，保证模拟的精确性。步数为1000，每步时间为0.002s，旋轮与工件之间有摩擦力而使旋轮的发生旋转，模拟时旋轮与工件之间的摩擦系数采用0.4。通过模拟，获得了应力应变分布。

（1）等效应力分布。图6为等效应力分布。由图6可以看出，在起旋阶段，旋轮前方未成形区和后方已成形区的等效应力值也较大。这是由于旋轮对前方的金属有拉弯的作用，拉应力传递到旋轮的已成形区域和未成形区域造成的。随旋轮进给量的增加，应力分布沿垂直旋压轨迹方向向外扩散。当旋轮旋入达到毛坯所要求的壁厚减薄率时，旋压变形进入稳定阶段。最大的等效应力集中于旋轮与工件接触区域。由图6（b）可以看出，等效应力沿中心轴方向的梯度最大，即金属沿着该方向的流动阻力最小。可见，旋压不仅对后方已加工区的影响很小，而且也不易在前方即将加工的区域产生材料的堆积。旋压过程工件中，最大等效应力随时间的变化如图7所示。由图7可以看出，在稳定工作阶段，最大等效应力变化不大，变形过程比较平稳［7］。

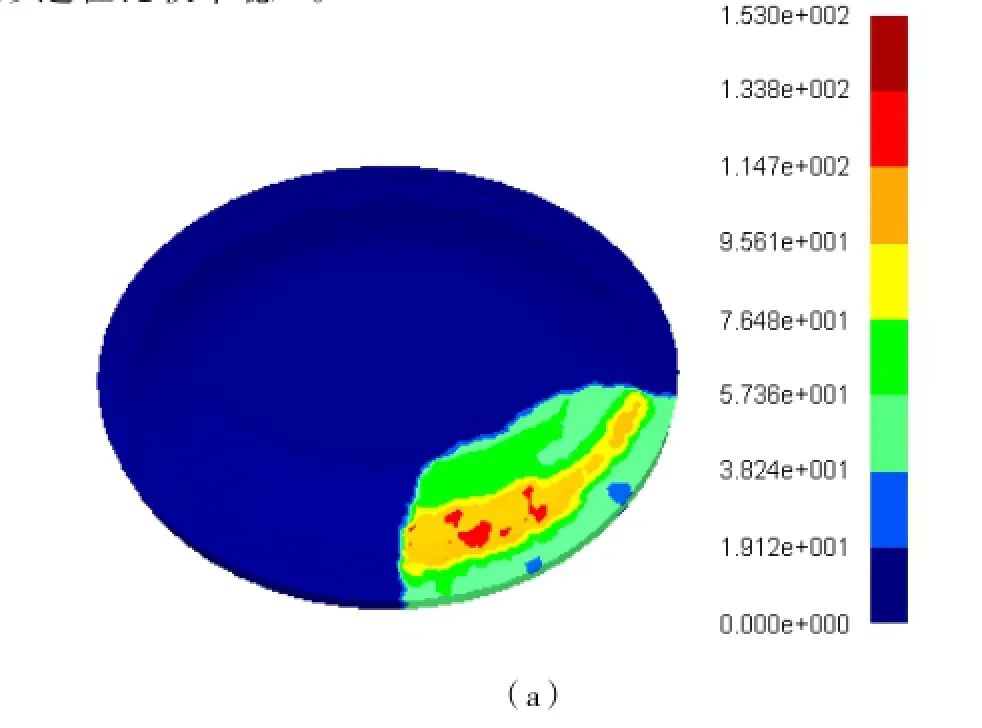
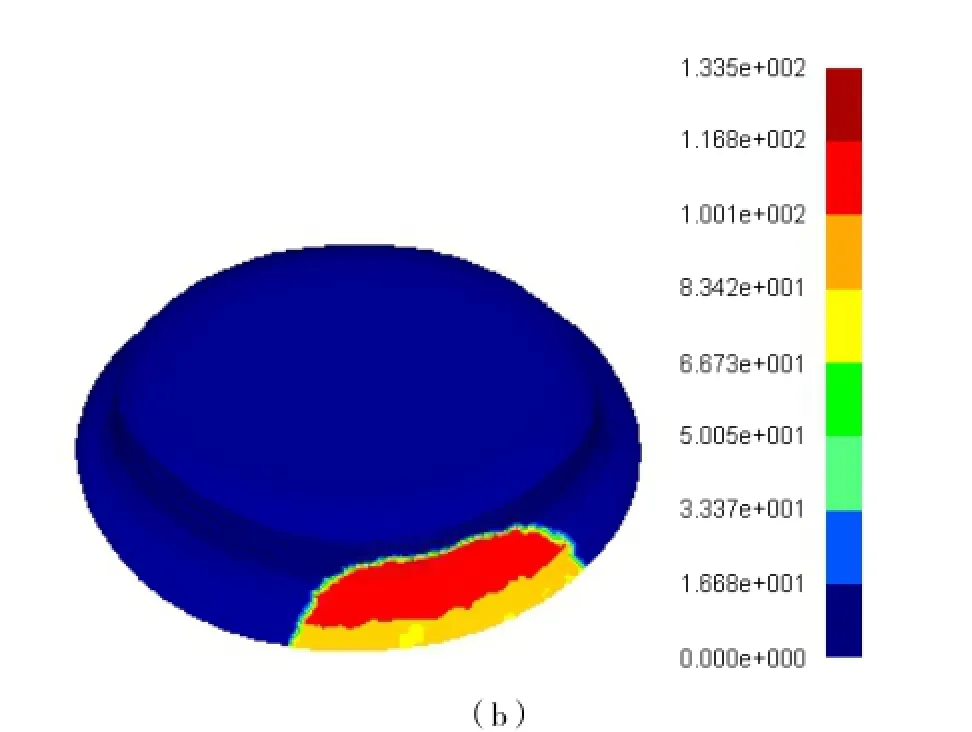
图6　等效应力分布

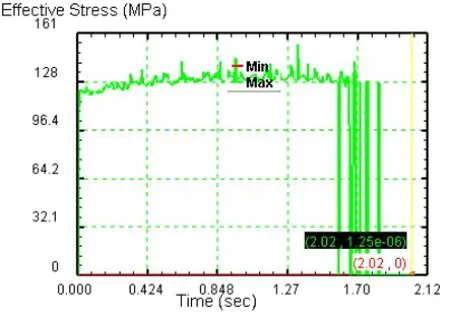
图7　等效应力

（2）等效应变分布。图8为等效应变分布。从图8可以看出，在起旋阶段，塑性应变分布较均匀，金属存在弯曲、拉伸和挤压多个方向的变形。当旋轮旋入毛坯达到所要求的壁厚减薄率后，旋压变形进入稳定阶段，塑性应变最大处分布在旋轮由椭圆长径过渡到椭圆短径的区域。这是因为在旋压过程中，坯料在旋轮的作用下发生弯曲和挤压变形逐渐贴合芯模.但是，由于芯模为椭圆形，在周向上变形不均匀，其中椭圆长径过渡到椭圆短径的区域内周向形状不均匀最显著，故而该区域内等效应变大［8］。

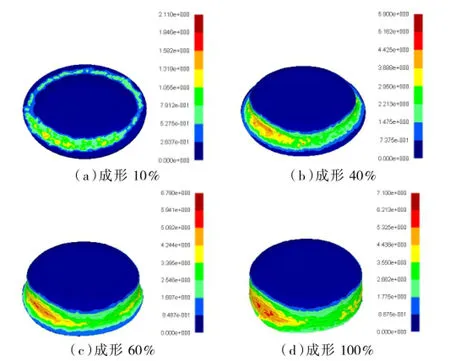
图8　等效塑性应变分布

3　毛坯形状对旋压结果的影响

生产中毛坯初始形状会对成形过程产生影响，因此本文进一步研究两种不同形状的毛坯对成形结果形状的影响。

图9为毛坯图，图10为工件最终变形图。从图9和图10可以看出，当毛坯是由芯模等比例放大的形状时，旋压结束后，底部边缘非常不平整，需要进一步加工修平，增加了加工成本和材料的浪费。而当毛坯是由 Dynaform反求出的形状时，旋压结束后，工件底部边缘较为平整。因此，椭圆筒形件旋压的毛坯形状并不是简单的芯模椭圆形状等比例放大。在生产过程中，可以以Dynaform反求出的毛坯为基础，根据实际情况进一步修改完善。

图9　毛坯图

图10　最终变形图

4　结论

本文运用Deform模拟椭圆筒形件旋压的成形过程，结论如下：

（1）椭圆筒形件旋压模拟过程中，运动轨迹由旋轮绕旋轮轴自转、绕芯模主轴公转和沿芯模主轴方向偏移的运动合成，计算结果稳定高效。

（2）Deform模拟中，旋压对已加工区的影响很小，并不易对在后面即将加工的区域产生材料的堆积，最大等效应力变化不大。坯料在旋轮的作用下发生弯曲和挤压变形逐渐贴合芯模，由于芯模为椭圆形，在周向上变形不均匀，其中椭圆长径过渡到椭圆短径的区域内周向形状不均匀最显著，故而该区域内等效应变大。

（3）椭圆筒形件旋压的毛坯形状并不是简单的芯模椭圆形状等比例放大，在生产过程中可以以Dynaform反求出的毛坯为基础，根据实际情况进行修改和完善。

［1］高田佳昭.日本呢最新回車云成形技术［J］.塑性加工（日本塑性加工学会志），2002，（11）：8-12.

［2］夏琴香.三维非轴对称零件成形工艺及设备［J］.新技术新工艺，2003，（12）：33-35.

［3］刘陶.基于DEFORM-3D的铝合金筒形件旋压成形过程数值模拟 ［J］.锻压技术：特种铸造及有色合金，2010，30（6）：508-510.

［4］赵云豪，李彦利.旋压技术与应用［M］.北京：机械工业出版社，2007.

［5］陈海涛，魏修亭，徐海泉，徐鹏.基于DEFORM-3D的轮辐旋压成形有限元模拟［J］.现代制造技术与装备，2012，（4）：1-2.

［6］梅瑛，牛朝勃，刘波，李瑞琴，张爱晨.铝合金筒形件强力正旋的应力应变分析［J］.机械设计与研究，2011，（1）：53-56.

［7］郝继东.变薄旋压工艺数值模拟及实验分析［D］.青岛：山东科技大学，2011.

［8］王凤彪.锥形件强力旋压壁厚的模拟预测及试验验证［D］.重庆：重庆大学，2014.

Numerical Simulation of Spinning Forming of Elliptical Tube Shaped Parts based on Deform

LU Lu
（College of mechanical and Electronic Engineering，Shandong University of Science and Technology，Qingdao 266000）

Application of deform 3D software established single roller is elliptic cylindrical elastic plasticity finite element model，by setting rotary wheel around the axle of the roller rotation，orbit around the mandrel spindle and along the offset of the mandrel axis direction of motion synthesis of the elliptic tube shaped part of the trajectory.By using Dynaform software to obtain the blank size，the distribution law of stress and strain in the process of spinning is obtained by the finite element simulation，and the influence of the blank shape on the forming process is analyzed.The results show that the effect of spinning on the processed area is very small，and it is not easy to accumulate the material in the area that is about to be processed at the back，and the maximum equivalent stress is not changed.In the region of the elliptical length，the circumferential shape is not even and the most significant，and the effect becomes larger in the region.In the actual production process，the spinning of elliptical cylindrical parts can be used as the basis of the blank of Dynaform reverse，and the modification and improvement are carried out according to the specific conditions.

Elliptic cylinder，DEFORM，Equivalent stress，E-quivalent strain，Spinning forming