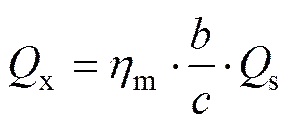单箱室波形钢腹板梁桥横向弯矩计算方法

黎雅乐，杨丙文，张建东



单箱室波形钢腹板梁桥横向弯矩计算方法

黎雅乐1, 2，杨丙文3，张建东1, 4

(1. 东南大学 土木工程学院，江苏 南京，210096；2. 南京航空航天大学 金城学院，江苏 南京，211156；3. 江苏省建筑工程质量检测中心有限公司, 江苏 南京，210028；4. 江苏省交通科学研究院股份有限公司，江苏 南京，211112)

为较简便地设计出波形钢腹板箱梁(BSW)桥的桥面板，基于框架分析法的基本原理，结合波形钢腹板箱梁的结构特点和力学特性，建立适用于单箱室波形钢腹板箱梁桥桥面板横向弯矩的计算方法，再对波形钢腹板箱梁和混凝土腹板箱梁在相同荷载作用下顶板的横向弯矩进行对比，对几座代表性的单箱室波形钢腹板箱梁桥顶板横向弯矩进行计算分析。研究结果表明：波形钢腹板箱梁桥的桥面板最大横向弯矩远高于同类混凝土腹板箱梁的横向弯矩峰值，提出的单箱波形钢腹板箱梁桥顶板横向设计弯矩的建议值可为今后同类波形钢腹板箱梁桥顶板尺寸拟定及配筋设计提供参考。

波形钢腹板箱梁(BSW)；框架分析法；箱梁顶板；横向弯矩

波形钢腹板箱梁桥发源于法国，由于结构自身的优点，该桥型已在世界各地得到广泛应用[1]。自2005年国内建成首座波形钢腹板PC箱梁桥——淮安长征人行桥至今，国内已建和在建的波形钢腹板PC组合箱梁桥已超过30座[2]。各国学者对该类结构的抗弯[3−4]、抗扭[5−7]、抗剪[8−10]和结构稳定性[11−12]等方面已取得了较多研究成果，但对桥面板局部荷载作用下的受力特性和横向内力分析方法的研究较少，箱梁的横向刚度通常都小于纵向刚度，而波形钢腹板箱梁由于其截面抗畸变性能较弱[13]，其桥面板横向内力与混凝土箱梁存在较大差异。已有的波形钢腹板箱梁桥面板的研究多集中在多箱室梁横向分布系数[14]和最不利位置[15]、箱梁顶板有效分布宽度[16−17]等方面。目前，国内在初步设计时对于波形钢腹板箱梁的顶板合理厚度及横向配筋设计没有明确依据。我国的波形钢腹板箱梁(BSW)桥的设计常参考国外已建桥梁或通过电算再依照混凝土桥梁设计规范[18]进行复核，常规桥梁设计软件如桥梁博士等对箱梁横向受力无法准确模拟，黄浩等[19]在迈达斯软件中实现了基于梁单元框架模型的横向内力计算，但专业设计软件多为“黑箱”，软件中波形钢腹板箱梁结构计算模块发展时间较短，是否能准确地仿真波形钢腹板与顶底板之间的约束关系值得探讨。若依靠通用有限元软件进行设计验算，则耗时较长且后处理繁琐。在初步设计阶段，急需一种横向内力的手算方法。本文作者基于框架分析法的基本原理，建立适合于单箱室波形钢腹板箱梁桥顶板横向弯矩计算方法。

1 波形钢腹板箱梁框架分析法分析

框架分析法是将箱梁的空间三维问题简化为平面框架问题进行求解的一种方法，其原理是：在箱梁的纵向取单位长度的框架，保证框架与整个箱梁体的变形相协调的前提下采用结构力学方法进行分析[18]。在分析平面框架时，需要引入适当的支承条件，如图1所示。由于这些虚加的支承条件并不存在，所以它们所产生的作用将用与支承反力大小相等但方向相反的力消除。令这些力为q=R(=1，2，3，4)，如图2所示，并可分解为对称荷载sym与反对称荷载s和h。正对称荷载作用下截面的横向弯矩影响较小可忽略，因此，释放支承可视为对原箱梁结构施加反对称荷载。因此，可认为箱梁的横向弯矩为加支撑框架的弯矩与反对称无支撑框架的弯矩的叠加。加支撑框架的弯矩可用弯矩分配法等结构力学方法求得，而对于波形钢腹板箱梁截面而言，反对称无支撑框架的弯矩的计算有待进一步分析。

图1 支承形式

图2 荷载及其分解示意图

1.1 内力平衡关系

在反对称荷载作用下箱梁会产生畸变，畸变翘曲应力在横截面上呈线性分布，如图3所示。设角点由畸变产生的翘曲应力为，角点由畸变产生的翘曲应力为，其比值为。这些翘曲应力在组成箱梁的各板平面内形成畸变内力矩，由于波形钢腹板纵向弹性模量较小，在波形钢腹板箱梁中，一般认为腹板不承担弯矩，设顶板、底板、腹板的畸变内力矩分别为，和，则：

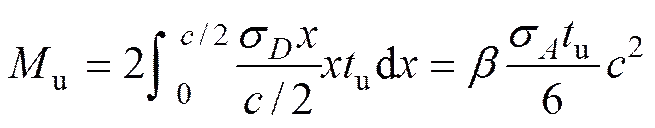
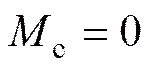
o和分别为横断面上腹板长度、顶板宽度、顶板在腹板间宽度、底板在腹板间宽度，如图3所示。

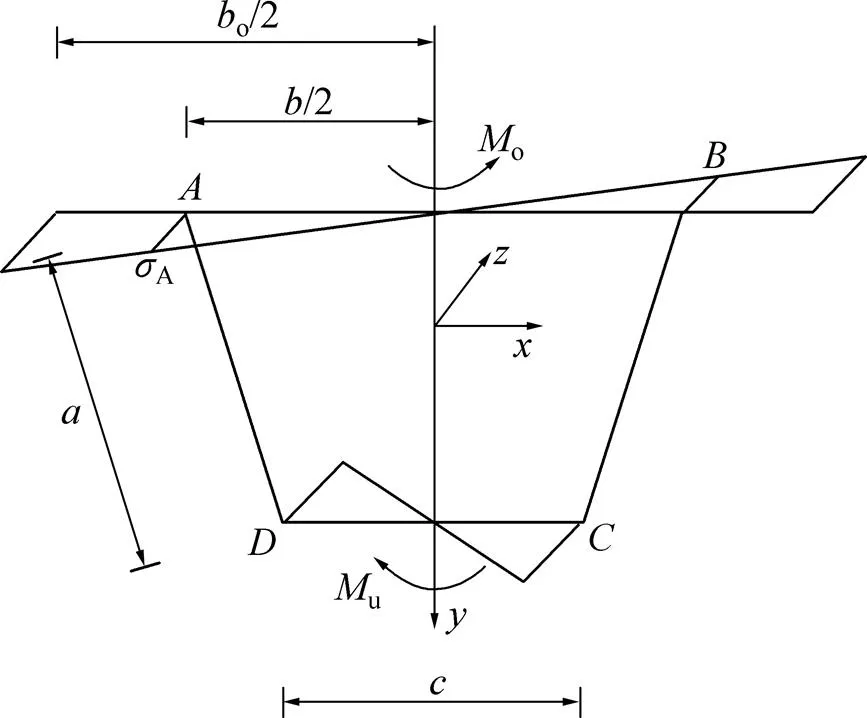
图3 顶、底板畸变翘曲应力分布

1.2 内力及位移分析

在反对称荷载作用下，顶、底板的反弯点位于中心线上，设反弯点处的剪力分别为s和x，设腹杆件反弯点处的剪力为h，腹板的反弯点将腹板分为上、下2段，其高度的比例为1/m，如图4所示。

由各角点弯矩平衡可以得到各剪力的关系[18]为：

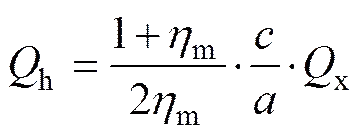
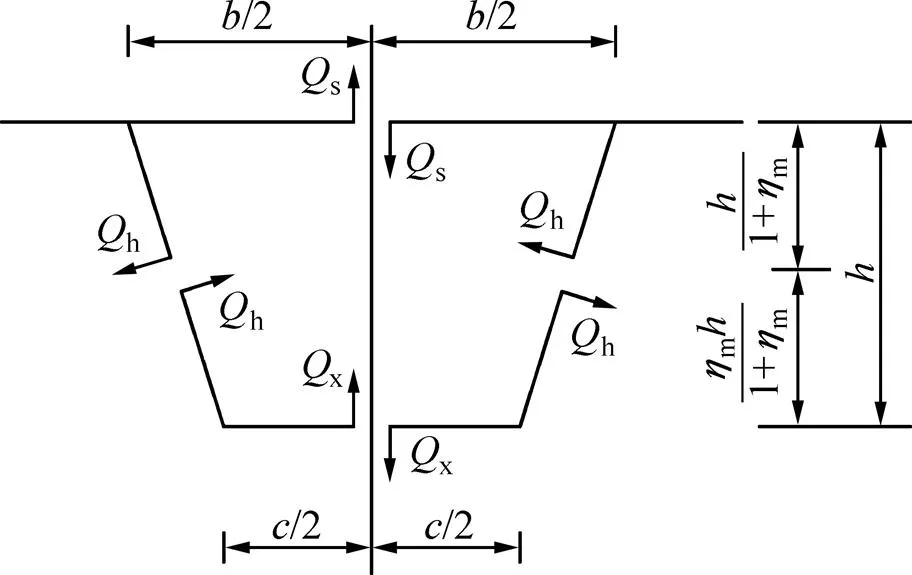
图4 框架剪力