基于脆性熵的城市生命线灾损敏感性评估

刘爱华，吴超，徐文彬



基于脆性熵的城市生命线灾损敏感性评估

刘爱华1，吴超2，徐文彬1

(1. 广东工业大学环境科学与工程学院，广东广州，510006；中南大学资源与安全工程学院，湖南长沙，410083)

为了对城市生命线在灾害作用下的高度敏感性和耦合放大性进行全面的评估，引入脆性熵理论对城市生命线的灾损敏感性进行研究。在界定承灾体脆弱性和灾损敏感性概念的基础上，构建城市生命线灾损敏感性评价指标体系。在综合考虑网络节点的结构重要性和功能重要性的基础上，用网络的实际均衡熵与系统最大熵的比值建立单功能网络结构灾损敏感性指数的计算模型。从影响机理入手，对各生命线子系统之间不同作用类型进行划分，并构造相应的布尔型矩阵，利用脆性熵理论分析各生命线子系统之间的脆性关联程度，得到生命线系统整体网络结构的灾损敏感性计算模型。从质量灾损敏感性和网络结构灾损敏感性2个方面建立城市生命线的灾损敏感性评估模型。研究结果表明：各子系统之间的脆性关联会使得城市生命线的灾损敏感性增加；在受到灾害破坏时，通讯系统与其他子系统的脆性关联最大，在灾后应该抢先修复。

城市生命线；灾损敏感性；评估方法；节点；脆性熵

城市生命线系统的概念是20世纪70年代DUKE等[1]在考察电力、交通、供水及煤气等系统震害以及对整个城市功能的影响后提出来的，认为这些基础设施对城市的经济和社会生活具有特别重要的作用，因而称之为“城市生命线系统工程”，对生命线系统的高度依赖已经成为现代化城市的重要特征之一。随着城市化程度的不断提高、城市功能的日益复杂化和多样化，与城市生命线相伴出现的灾害隐患越来越多，而且城市生命线系统的灾害事故具有破坏严重、耦合放大性、次生灾害突出、社会影响大等特点。灾害风险研究是构建综合防灾减灾体系的基础和依据。而承灾体的脆弱性评估又是灾害风险评估的核心问题，也是国际上各种灾害风险评估方法共同探讨的热点问题[2]。为了预防和控制城市生命线灾害事故，国内外许多学者对城市生命线的脆弱性也进行了较深入的研究，主要集中在2个方面：一是地震灾害作用下城市生命线系统的脆弱性分析和评估[3−5]；二是供电、交通等生命线子系统在地震、洪水等单灾种作用下脆弱性评估方法的研究[6−8]。城市生命线系统具有复杂网络结构特点，且不同类型系统在功能上具有耦联性。这种耦联性由造成结构破坏的随机变量或随机过程之间的相关性引起，也可由结构破坏的传递性引起。因此，城市生命线脆弱性评估如果把单功能子系统割裂开来进行评估，往往会因为忽略系统这种耦联性而使得评估结果出现偏颇，单一灾种条件下的脆弱性分析则会因忽略灾害的链式效应和放大效应而出现表征的局限性，不利于城市综合防灾减灾体系的构建。针对上述问题，本文作者在对脆弱性和灾损敏感性的概念进行界定的基础上，提出用均衡熵表征单功能网络结构的脆弱性，并应用脆性熵理论求解出各生命线子系统的脆性关联程度，结合城市生命线的质量灾损敏感性，构建生命线系统的灾损敏感性评估模型。

1 城市生命线灾损敏感性评估指标体系的构建

许多研究把承灾体的灾损敏感性和脆弱性等同为一个概念，固然灾损敏感性和脆弱性都是相对承灾体而言的，但两者的内涵是不一样的。脆弱性是指在一定灾变条件下受灾体的抗御能力及其损毁程度。脆弱性包括承灾体的物理暴露性e、灾损敏感性d和应灾能力s3个方面[9]。物理暴露性是指承灾体暴露在致灾因子影响范围之内的数目或价值；区域应灾能力是指区域社会为了预防某种灾害的袭击而对承灾体采取的各种防御措施的力度；灾损敏感性是指承灾体在遭受一定致灾强度的灾害打击后易于受损的程度，它反映了承灾体因自身的物理特性而对致灾因子破坏作用的抵御能力。物理暴露性可通过承灾体的管理部门获取相应的统计数据而确定，因此灾损敏感性是对各承灾体脆弱性分析的重点和难点。

在布设城市生命线时，许多敷设在地下，受地震的影响较大，因此生命线本身的抗震性能是影响其质量灾损敏感性的重要因素，另外使用年限、工程质量、以及生命线的网络结构等也是影响其质量灾损敏感性的主要因素。根据王飞[10]的研究成果，1985年以前投资建设的基础设施因使用年限较长而抗灾性能较差；而1994年以后投资建设的基础设施抗灾性能相对较好；近5年基础设施投资额年均增长率则反映了目前的城市生命线设施状况和发展水平。

城市生命线以整体网络结构形式支持着城市的系统功能，因此衡量生命线网络结构的灾损敏感性既要考虑各子系统的网络可靠性，也要考虑各子系统之间的关联性对整体网络结构所造成的影响。单功能网络结构的可靠性可从网络的拓扑结构性、系统的供给能力等多方面进行度量[9, 11]。生命线网络结构中脆性的存在，是生命线系统事故具有耦合放大特性的根本原因，因此，在对生命线系统的灾损敏感性进行评估时，必须对其脆性进行评估。由此，可建立城市生命线灾损敏感性评估的指标体系，如图1所示。

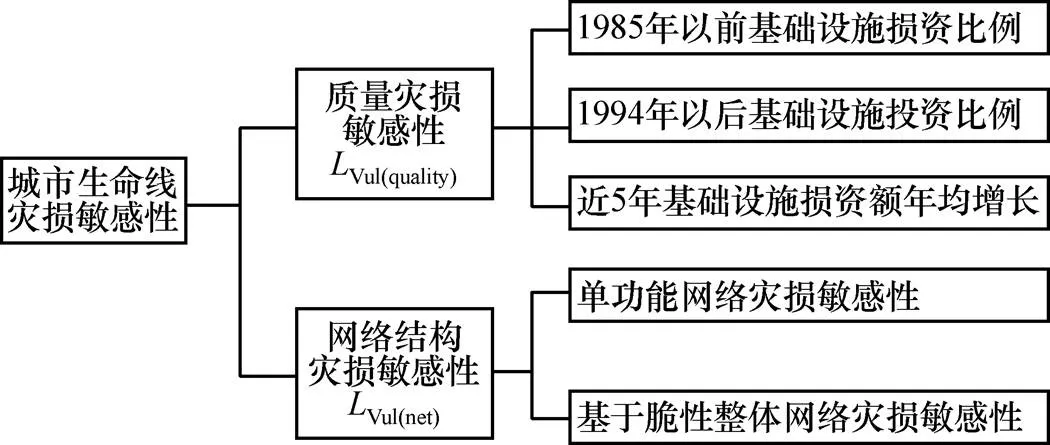
图1 城市生命线灾损敏感性评估指标体系

2 单功能网络的灾损敏感性评估

城市生命线系统结构庞大、功能复杂。在结构上，呈现分块又分层的立体结构；在运行过程中，呈现出明显的非线性和高维特征，因而城市生命线系统是一个动态多变的复杂网络系统[12−13]。城市生命线网络已经发展成为世界上最复杂的人造网络之一，而每个单功能子系统在结构上又有自己独立的网络结构。

2.1 网络节点的结构重要性

在每个单功能网络结构中，每个节点的地位是不同的。以交通网络为例，某些交通节点在发生事故时只会影响局部的交通畅通，而某些交通节点在发生事故时会导致整个交通系统的瘫痪。为了衡量这些节点在网络拓扑结构中的重要程度以及影响能力，引入中介中心性的概念[11, 14]。在网络结构中任意节点的中介中心性g定义为：设某网络拓扑结构中的一条路径，开始于节点为，中间经过一系列的节点和边，终止于节点，为其中的一个中间节点[15−17]，设(，)为节点到节点所有最短路径的总数，在这些路径中，通过节点的路径数为c(，)，则记g为g(，)，可表示为

g(，)即表示节点在网络中的结构重要程度。

2.2 网络节点的功能重要性

在网络结构中，有些路径输送的资源量很大，该路径以及路径上的节点一旦遭受破坏，对系统的影响很大。因此衡量网络节点重要性的另一个指标就是节点所在路径传递的信息流，称之为功能重要性，其实际是指节点所在路径传递介质的能力，可用连接边强度来表征。对于供水、供气等资源供给的管网系统，连接边的连接强度就是管网中的流压。设任意2个连通节点和的连接边强度用表示，而且在节点与之间存在连接强度大于0的一个边的序列，把和连接在起来[10−11]：

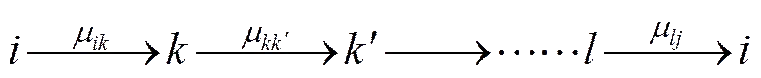
该序列被称为节点与的最短路径，记为。

定义为与之间最短路径的连接强度，那么该路径上各节点的功能重要度为

2.3 单功能网络的灾损敏感性评估

节点的结构重要性和功能重要性综合重要性都影响着整个网络的灾损敏感性，因此，要综合考虑。引入综合重要度予以衡量，定义为

如果网络系统中存在少数几个综合重要度极高的节点，则该网络称之为“不均衡”网络，称综合重要度极高的节点为“核心节点”。在此网络中，核心节点一旦失效，会导致系统资源的供给量远远小于正常的需求量，从而影响广泛，严重的可能导致整个网络崩溃或瘫痪。对于不存在核心节点的“均衡”网络，就不会因为某个节点的失效而影响系统的整体运行。可见网络节点分布的均衡性能有效反映单功能网络的灾损敏感性[10]。德国物理学家克劳修斯所提出的热力学概念“熵”也被广泛应用于系统失序现象的表征。熵越大，表示对象越无序，而系统越均衡。由此可推，在网络结构中，同层节点综合重要度的熵越大，表明网络也就越均衡[11]，因此，可用“熵”来反映节点在网络结构中分布的均衡性。在此引入“均衡熵”的概念对生命线单功能网络系统的灾损敏感性进行评价在理论上具有可行性。

2.1.1 高龄 患者73岁，老年患者组织和器官功能退行性改变，成纤维细胞的分裂周期也明显延长，免疫功能减退，致使伤口愈合的过程延迟。

设某单功能网络系统共有个节点，从源点到汇点的最短路径共有条。分别统计计算每个节点的结构重要度，并把具有结构重要度相同节点组成节点集，设共有个节点集，第个节点集中有个有节点，各个节点集的综合重要度分别为1，2，…，H。首先对各节点集节点的综合重要度进行归一化处理，设归一化处理后各节点的综合重要度分别为，则

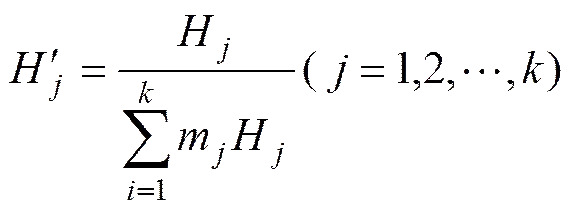
其中：m为第个节点集中的节点数。

根据熵原理，当时，系统熵取得最大值，即

那么网络系统实际的均衡熵的计算式为

如果网络系统实际均衡熵与最大熵的比值越接近1，表明网络的均衡性越好，网络系统的可靠性也就越高；反之，网络系统的可靠性越低，灾损敏感性也越大。因此，网络系统的灾损敏感性可表示为

3 基于脆性整体网络结构的灾损敏感性评估

3.1 城市生命线系统间相互影响

城市生命线系统中的各个子系统之间存在相互作用，且作用方式各异，关系非常复杂。以各子系统的相互作用机理为基础，对相互作用类型进行科学分类是厘清其复杂关系的有效方法。因此，从作用机理入手，结合子系统间相互影响的事故案例，将生命线系统的相互作用划分为4种类型：

1) 功能型相互作用，是指一个子系统功能的正常发挥依赖于与之关联的其他子系统功能的正常发挥，也就是当与之关联的子系统功能失效时，会导致该系统的功能无法正常发挥。典型的案例有，供电中断会使得水泵无法运转，水泵的停止运转则会进一步导致供水系统的功能失效；天气寒冷导致供暖增加，从而导致燃气紧张等。

2) 布设型相互作用，即因为子系统的相邻布设，导致一个系统受损时，而另一个系统也被破坏。例如，沿道路敷设的城市燃气、供水等地下管道受到破坏时，往往会引起道路系统的损坏，同样在道路遭受破坏时，也可能会导致燃气、供水等地下管道的损坏。

3) 替代型相互作用，即一个系统的功能可用与之关联的其他子系统的功能进行替代，因此当系统失效时，会造成与其功能替换子系统的过量需求。例如，供气系统中断，作为可替换能源的电力的消耗将明显增加。

4) 恢复型相互作用，即破坏后在功能恢复与修复进程中会彼此影响，当多种生命线系统失效时，其中某种生命线系统会影响其他生命线系统的修复进程。例如电力系统破坏，其他系统恢复都会变得很困难。

相互作用的类型划分是相互影响机理的具体化。根据如上分类方式，对供电、供气、供水、交通、通讯五个典型生命线系统之间的相互作用关系进行分析，它们之间在功能严重失效情况下彼此间的相互作用类型及对应的影响方式如表1所示[18−19]。

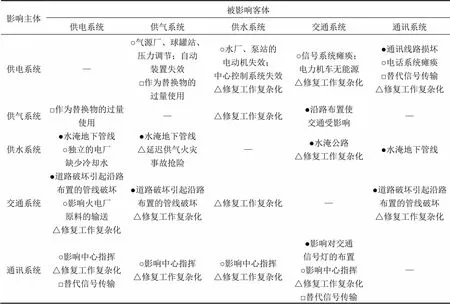
表1 生命线系统功能严重失效时的相互作用特性

注：●—布设型相互作用；○—功能型相互作用；△—恢复性相互作用；□—替代型相互作用。

3.2 基于脆性熵的生命线系统脆性分析

脆性是指材料在外力作用下(如拉伸、冲击等)仅产生很小的变形即断裂破坏的性质[20]。后来人们发现，复杂系统也表现出这一特性，因此，逐步把脆性的定义和研究方法引申到对复杂系统的特性研究当中。其相应的定义为：复杂系统在内、外因素的扰动作用下，出现部分崩溃，进而影响到与之关联的其他部分，并产生连锁崩溃效应，最终导致整个复杂系统崩溃的特性，称之为脆性[21]。

可由上述研究可知：城市生命线系统是一个动态的复杂系统，各子系统的关联性必然会导致系统内脆性的存在。因此，在对城市生命线的灾损敏感性进行评估时，必须考虑系统的脆性，以免割裂或忽视了各系统之间的关联。根据脆性理论思想，结合生命线子系统的相互影响分析，利用熵理论对城市生命线子系统之间的脆性关联进行定量处理和计算，再结合单功能子系统的灾损敏感性，对城市生命线系统的整体灾损敏感性进行评价。

1) 脆性联系熵。如果一个子系统因为干扰而发生事故且不能正常工作，与之脆性关联的其他子系统必将会受到影响，表征其状态的变量也将随之改变。假设因与脆性相关而受到影响，表征的个状态向量中，变量y(1＜＜)发生了变化，对应于该状态变量的功能丧失，无法正常工作，则认为变量y与子系统为脆性同一[11, 22−23]；没有受到影响的状态变量与子系统为脆性对立。随时间变化呈现不稳定状况的状态变量与子系统构成脆性波动。子系统的任意变量y可能出现上述3种情况的概率分别是，，，则3个概率和为1。引入熵理论，则分别为脆性对立熵、同一熵、波动熵。其相应的定义如下：

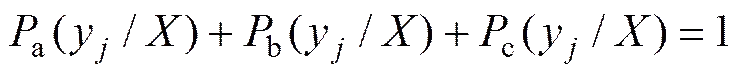
脆性同一熵的定义式为

脆性对立熵的定义式为

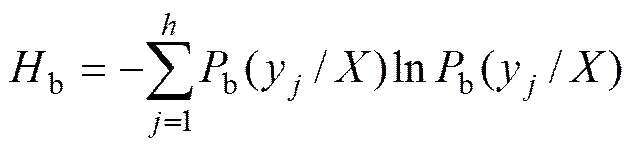
脆性波动熵的定义式为

实际上，子系统在的关联作用下，应该是脆性同一、脆性对立和脆性波动的综合。因此子系统与子系统的脆性联系熵为

式中：a，b，c分别为脆性同一、脆性对立和脆性波动的权重系数，采用燕尾突变级数法可以确定相应的值：

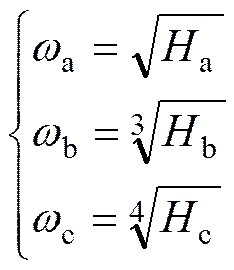
在系统中，存在一定的概率分布组合，使H达到最大，表明此时子系统受到的影响最大，而崩溃的可能性也最大。与子系统类似，也可以定义其他子系统脆性联系熵的相关概念。

2) 生命线系统的相互作用。根据脆性联系熵的定义，在城市生命线系统当中，各子系统间的布设影响可表征为脆性同一，替换作用可表征为脆性对立；而功能影响和恢复影响可表征为脆性波动。在事故状态下城市生命线子系统间的脆性关联特征可用布尔型矩阵来表示，矩阵中的0表示彼此间没有影响，1表示彼此间存在相互影响，那么不同类型影响方式的布尔型矩阵如下。

布设影响：

功能影响：

恢复影响：

替换作用影响：

城市生命线子系统间的脆性联系熵计算过程 如下。

1) 首先对每个矩阵的列求和，得到它们耦合之后的综合矩阵：

2) 对综合矩阵的每列再求和，就可得到各个子系统与其他子系统的影响关联：供电系统为9，供气系统为8，供水系统为7，交通系统为7，通讯系统为7。

3)最后再计算各子系统的脆性同一、脆性对立和脆性波动所对应的概率a，b和c及其相应的熵a，b和c等参数，结果如表2所示。

表2 脆性关联计算结果

由表2可知：各生命线子系统的脆性关联从小到大排列顺序为：供水系统，交通系统，供气系统，供电系统，通讯系统。表明与其他子系统脆性关联最大的是通讯系统，是灾后应该抢先修复的子系统，以此来降低由于通讯系统与其他系统关联而带来的连锁影响。

4 城市生命线的灾损敏感性计算

4.1 生命线网络结构的灾损敏感性评估

作为单功能网络系统的城市生命线子系统，网络结构本身存在一定的灾损敏感性，而脆性关联的存在会导致城市生命线系统整体的灾损敏感性进一步增加，因此对生命线系统的整体灾损敏感性进行分析时，既要考虑各个子系统的灾损敏感性，还必须考虑脆性关联所引发灾损敏感性的增量。在对整体灾损敏感性进行评估时，可把每个子系统的灾损敏感性视为整个系统灾损敏感性一种表现途径，即各个子系统类似并联的几个系统，另外，把每个子系统自身崩溃而引发的其他系统崩溃的情况也统计在内，由此生命线系统整体网络结构的灾损敏感性可表示为

其中：为生命线系统网络结构的灾损敏感性指数；为子系统的网络灾损敏感性指数；为各系统的脆性关联熵的归一化值。

由上述分析可知：随着城市化程度的提高，城市各子系统之间的功能、恢复、替换等交互影响将会更更加复杂化，因此生命线各子系统之间的脆性关联熵只会进一步增加，而很难降低。不过可以通过方案设计使布设更加合理从而降低彼此间的脆性关联度。通过网络结构优化设计，在保证功能的基础上尽可能提高网络的综合均衡性则是降低生命线整体网络结构灾损敏感性最有效的措施。

4.2 城市生命线的灾损敏感性计算

综合考虑各项指标，城市生命线灾损敏感指数的计算方法如下：

5 应用实例

5.1 某城市生命线工程质量灾损敏感性评估

某东南部沿海城市，陆地面积约1 700 km2，拥有公路通车里程达1 017 km，其中高速公路4 km，1级公路283 km，2级公路47 km，3级公路440 km，4级公路214 km，等外路34 km；公路网密度达62.4 km/100 km2；拥有汽车客运2级站4个，4级站7个，简易站5个。公共供水能力为34 376万m3，供水管路总长度为2 890 km。天然气供气总量为28 306万m3，供气管道长度32.9 km，液化石油气供气总量 160 000 t，供气管道长度134.2 km。发电装机容量为3 067 736 kW。根据该市2012年的统计年鉴，该市城市生命线质量灾损敏感性各评价指标参数如表3所示。

表3 城市生命线质量灾损敏感性各评价指标参数

采用该市所在省份其他所有地级市作为比对对象，并对指标进行标准化处理，再结合权重得到该市的质量灾损敏感性指数=0.236。

5.2 网络结构的灾损敏感性评估

现以该市的供水管网系统为对象，对单功能网络的灾损敏感性评估的计算过程予以说明。为计算方便和简明，案例只对该市的主干管网进行计算，全管网的供水主要由泵站提供，而高地水池只是为了缓解用水高峰时段临时补充的泵站压力，故在此不考虑其对管网的作用。简化后的供水管网如图2所示。

图2 供水系统网络结构图

将该网络看成单源单汇结构。其中节点1与20，节点17与20之间均为单向流通线路，对该网络的各节点进行网络结构重要性和网络功能重要性分析，可以得到：从源点30到汇点0={10,11, 29}共有7条最短路径，其他各相关参数如表4所示。

表4 供水管网各网络节点参数

根据表1所得的网络节点参数，可计算出该市供水网络的实际均衡熵、最大熵和单功能网络的灾损敏感性指数分别为：=3.213，max=3.367，G−Vul=0.046。用同样的方法，可得该市供电、供气等其他几个子系统的灾损敏感性参数如表5所示。

表5 各子系统的网络结构灾损敏感性参数

在获得各单功能网络结构的灾损敏感性指数后，再结合前面所得到的各子系统的脆性关联熵，即可得整个生命线系统的网络结构灾损敏感性指数为：=0.359。如城市生命线质量敏感性指数、生命线系统网络结构的灾损敏感性指数的权重系数0.6和0.4，则城市生命线灾损敏感指数为：s=0.285。

5.3 结果分析

由于目前没有关于城市生命线灾损敏感性的等级划分标准，借鉴建筑物的易损性划分标准[24]，当灾损敏感性指数为0.285时，灾损敏感性等级为B，抗灾能力为中级。由于该市是一个新建城市，政府对基础建设较为重视，因此其质量灾损敏感性相对较低。

从单功能网络结构的灾损敏感性来看，交通子系统的网络结构灾损敏感性最大，这与该市一到节假日或因为灾害事故交通易出现拥堵的实际状况是吻合的，表明该市应从网络结构入手对城市交通作进一步的规划。从计算案例可知该市供水网络的均衡性很好，节点的重要程度相当，因此，整个网络的灾损敏感性较低。但在该网络系统中也存在一些“核心节点”，其重要度相对较高的，如20号节点，其网络综合重要度为9/28，相对其他节点较高，表明这些节点的灾损敏感性比较高，需提高其抗灾能力，以防止不确定灾害破坏发生时，由于这些节点的损坏，给系统整体功能恢复带来不利影响。

当不考虑各子系统的关联性，生命线整体的网络结构灾损敏感性为0.274，当考虑各子系统的关联性时，生命线整体的网络结构灾损敏感性为0.359，结果表明各子系统之间存在的脆性关联，使得整个生命线的网络结构灾损敏感性有较大的提高。

6 结论

1) 城市生命线的灾损敏感性主要取决于生命线的质量灾损敏感性和网络结构灾损敏感性。因此可从这2方面对其灾损敏感性进行表征。

2) 以生命线节点的结构重要性和功能重要性为基础，界定了节点综合重要度的概念，提出了其计算方法。引入熵的概念，对单功能网络结构的灾损敏感性进行了表征。从城市生命线相互影响的机理入手，对各生命线子系统间的相互作用类型进行了划分，利用脆性联系熵理论，构造了不同作用类型的布尔型矩阵，提出城市生命线子系统脆性关联的计算方法。

3) 把每个子系统的灾损敏感性都视为整个生命线系统灾损敏感性一种表现途径，并考虑由于各子系统之间的脆性关联对灾损敏感性的扩大化影响，通过可靠性的计算方法，构建了生命线的灾损敏感性综合评估模型。模型更加客观、全面地反映了生命线系统的灾损敏感，能为城市风险评估评估提供技术支撑。

[1] DUKE C M, MORAN D F. Guidelines for evolution of lifeline earthquake engineering[C]//Proceeding of US National Conference on Earthquake Engineering. Oakland: Earthquake Eng Res Inst, 1975: 367−376.

[2] 石勇. 灾害情景下城市脆弱性评估研究: 以上海市为例[D]. 上海: 华东师范大学资源与环境工程学院, 2010: 4−10.
SHI Yong. Research on vulnerability assessment of cities on the disaster scenario: a case study of shanghai city[D]. Shanghai: East China Normal University. College of Resources and Environment Science, 2010: 4−10.

[3] 操铮, 刘茂, 许同生. 城市生命线系统的地震网络可靠性研究[J]. 自然灾害学报, 2011, 20(6): 32−39.
CAO Zheng, LIU Mao, XU Tongsheng. Research on seismic network reliability of urban lifelines system[J]. Journal of Natural Disasters, 2011, 20(6): 32−39.

[4] 白广斌. 基于GIS的城市生命线震害预测系统应用研究[D]. 大连: 大连理工大学土木工程学院, 2007: 22−48.
BAI Guangbin. AN predicting earthquake disaster system of urban lifeline research based on GIS[D]. Dalian: Dalian University of Technology. School of Civil Engineering, 2007: 22−48.

[5] WANG Xuan. Study on earthquake emergency readiness capability evaluation of urban lifeline system[J]. Shenyang: Journal of Northeaster University (Science and Technology), 2010: 987−991.

[6] 王博. 复杂电力系统安全风险及脆弱性评估方法研究[D]. 武汉: 华中科技大学电气与电子工程学院, 2011: 52−65.
WANG Bo. Research on security risk and vulnerability assessment methods of complicated power system[D]. Wuhan: Huazhong University of Science and Technology. School of Electrical and Electronic Engineering, 2011: 52−65.

[7] 胡一竑, 吴勤旻, 朱道立. 城市道路网络的拓扑性质和脆弱性分析[J]. 复杂系统与复杂性科学, 2009, 6(3): 69−75.
HU Yihong, WU Qinmin, ZHU Daoli. Topological properties and vulnerability analysis of spatial urban street networks[J]. Complex Systems and Complexity Science, 2009, 6(3): 69−75.

[8] 尹洪英. 道路交通运输网络脆弱性评估模型研究[D]. 上海: 上海交通大学安泰经济与管理学院, 2011: 37−90.
YIN Hongying. Research on the evaluation model of road transportation network vulnerability[D]. Shanghai: Shanghai Jiao Tong University. Antai School of Economics & Management, 2011: 37−90.

[9] 刘爱华. 城市灾害链动力学演变模型与灾害链风险评估方法的研究[D]. 长沙: 中南大学资源与安全工程学院, 2013: 49−93.
LIU Aihua. Research on the dynamics evolution model of urban disaster chain and the risk assessment method of disaster Chain[D]. Changsha: Central South University. School of Resources and Safety Engineering, 2013: 49−93.

[10] 王飞. 城市地震危害性模糊评价及地震损失预测评估[D]. 杭州: 浙江大学建筑工程学院, 2005: 8−30.
WANG Fei. Fuzzy evaluation of urban earthquake hazard and the prediction evaluation of the earthquake damage[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 2005: 8−30.

[11] 张明媛. 城市承灾能力及灾害综合风险评价研究[D]. 大连: 大连理工大学土木工程学院, 2008: 49−60.
ZHANG Mingyuan. Research on the assessment of disaster-carrying capability and disaster comprehensive risk in urban place[D]. Dalian: Dalian University of Technology. School of Civil Engineering, 2008: 49−60.

[12] 种鹏云, 帅斌. 基于复杂网络的危险品运输网络抗毁性测度分析[J]. 中南大学学报(自然科学版), 2014, 45(5): 1715−1723.
CHONG Pengyun, SHUAI Bin. Measure of hazardous materials transportation network invulnerability based on complex network[J]. Journal of Central South University (Science and Technology), 2014, 45(5): 1715−1723.

[13] 王甲生, 吴晓平, 陈永强. 不同信息条件下加权复杂网络抗毁性仿真研究[J]. 中南大学学报(自然科学版), 2013, 44(5): 1881−1894.
WANG Jiasheng, WU Xiaoping, CHEN Yongqiang. Invulnerability simulation of weighted complex networks with different information[J]. Journal of Central South University (Science and Technology), 2013, 44(5): 1881−1894.

[14] 刘博, 刘晓. 网络化生命线系统脆弱性分析与优化设计[J]. 中国安全科学学报, 2013, 23(3): 109−113.
LIU Bo, LIU Xiao. Vulnerability analysis and optimization design of networked lifeline system[J]. China Safety Science Journal, 2013, 23(3): 109−113.

[15] MOTTER KINNEY A E, LAI Y C. Cascade-based attacks on complex networks[J]. Physical Review E, 2002, 66(6): 65−102.

[16] KINNEY R, CRUCITTI P, ALBERT R, et al. Modeling cascading failures in the North American power grid[J]. The European Physical Journal B, 2005, 46(1): 101−107.

[17] WANG B, KIM B J. A high-robustness and low-cost model for cascading failures[J]. European Physics Letters, 2007, 78(4): 48−51.

[18] 汤爱平, 欧进萍, 张克绪, 等. 生命线系统相互作用下性态评价方法[J]. 哈尔滨工业大学学报, 2005, 37(2): 151−155.
TANG Aiping, OU Jinping, ZHANG Kexu, et al. Seismic performance assessment of lifeline systems[J]. Journal of Harbin Institute of Technology, 2005, 37(2): 151−155.

[19] 姚保华, 谢礼立, 火恩杰. 研究地震情况下生命线系统相互作用的综合方法[J]. 地震学报, 2004, 26(2): 193−202.
YAO Baohua, XIE Lili, HUO Enjie. A comprehensive study method for lifeline system interaction under seismic conditions[J]. Acta Seismologica Sinica, 2004, 26(2): 193−202.

[20] 荣盘祥, 金鸿章, 韦琦, 等. 基于脆性联系熵的复杂系统特性的研究[J]. 电机与控制学报, 2005, 44(2): 15−19.
RONG Panxiang, JIN Hongzhang, WEI Qi, et al. Research on the characteristic of complex system based on brittle link entropy[J]. Electric Machines and Control, 2005, 44(2): 15−19.

[21] 吴红梅, 金鸿章. 基于嫡理论复杂系统的脆性[J]. 中南大学学报(自然科学版), 2009, 40(增1): 347−351.
WU Hongmei, JIN Hongzhang. Brittleness of complex system based on entropy theory[J]. Journal of Central South University (Science and Technology), 2009, 40(Supp1): 347−351.

[22] 刘辉, 吴超, 李孜军, 等. 硫化矿石自燃灾害的脆性风险源[J]. 中南大学学报(自然科学版), 2011, 42(3): 752−757.
LIU Hui, WU Chao, LI Zijun, et al. Brittleness risk source for spontaneous combustion of sulfide ores[J]. Journal of Central South University (Science and Technology), 2011, 42(3): 752−757.

[23] WEI Huang. Coupling analysis of disaster bearing capacity of urban lifeline system based on brittleness entropy[J]. Computational Water, Energy, and Environmental Engineering, 2014, 3(3): 119−127.

[24] 葛全胜, 邹铭, 郑景云, 等. 中国自然灾害风险综合评估初步研究[M]. 北京: 科学出版社, 2008: 103−110.
GE Quansheng, ZOU Ming, ZHENG Jingyun, et al. A preliminary study on the comprehensive evaluation of natural disaster risk in China[M]. Beijing: Science Press, 2008: 103−110.

(编辑 陈爱华)

Damage sensitivity evaluation ofurban lifeline based on brittleness entropy

LIU Aihua1, WU Chao2, XU Wenbin1

(1. School of Environmental Science and Engineering, Guangdong University of Technology, Guangzhou, 510006, China;2. School of Resources and Safety Engineering, Central South University, Changsha, 410083, China)

To conduct the comprehensive assessment for the high sensitivity and the coupling amplification of urban lifelines during disasters, the theory of brittleness entropy was applied to study the damage sensitivity of urban lifelines. On the basis of defining the concept of the vulnerability of and damage sensitivity of hazard-affected bodies, the evaluation index system of damage sensitivity of urban lifelines was built. After comprehensively considering the importance of the structure and the function of lifeline network nodes, the calculation model of the damage sensitivity index of mono-functional network structure was established with the ratio of the actual equilibrium entropy to the maximum entropy of the urban lifeline network. Starting from the impact mechanism, the Boolean matrix of the different kinds of influence ways was constructed according to the different mutual influence methods between the lifeline systems. The brittleness relevance degree of the lifeline subsystems was analyzed using the theory of brittle entropy. And the model was gotten to calculate the damage sensitivity of the whole network structure of urban lifeline. The damage sensitivity evaluation model of urban lifeline was established from two aspects of the quality damage sensitivity and the network structure damage sensitivity. The results show that the brittleness connection between the subsystems can increase the damage sensitivity of urban lifeline. The entropy of brittleness connection is the largest between communication system and other subsystems. After the disaster, it should be first repaired.

urban lifeline; damage sensitivity; assessment method; node; brittleness entropy

10.11817/j.issn.1672-7207.2016.08.034

X9

A

1672−7207(2016)08−2793−09

2015−10−15；

2015−12−28

国家自然科学基金资助项目(51508110)(Project(51508110) supported by National Natural Science Foundation of China)

徐文彬，教授，博士，从事安全评价、事故模拟和应急方面的研究；E-mail：xuwenbin@tom.com