应变软化圆形隧道围岩的逐步量纲一化应力分析方法

蒋武军，邹金锋



应变软化圆形隧道围岩的逐步量纲一化应力分析方法

蒋武军1，邹金锋2

(1. 湖南省高速公路管理局，湖南 长沙，410001；2. 中南大学 土木工程学院，湖南 长沙，410075)

基于线性Mohr−Coulomb强度准则，采用量纲一化分析方法，改进应变软化围岩应力位移求解的逐步应力分析法。通过将软化围岩塑性区分为有限个圆环，对每个圆环求解其应力和应变增量，得到软化围岩应力和位移解。利用现有的理论解验证该方法的正确性和可靠性。通过数值计算和参数分析，揭示部分参数对围岩应力和位移的影响规律。研究结果表明：当圆环数量=500时，逐步量纲一化应力解与精确解吻合度较高；塑性区随临界塑性应变偏差增大而减小，当增加到某一定值时，围岩内部不存在残余区；塑性半径及围岩位移随着的减小而不断增大，当为0时，软化围岩近似于脆性状态。

应变软化；逐步应力法；Mohr−Coulomb强度准则；圆形隧道

在均质岩土圆孔隧道开挖过程中，对围岩的应力与应变进行研究是解决岩土工程问题的基础。由于在开挖过程中位移变化取决于应力路径，一般采用非线性方法求出可靠的解，而在目前研究中，弹塑性分析方法被广泛使用[1−2]，此前研究者普遍采用Mohr−Coulomb(M−C)强度准则对岩土体的弹塑性进行分析。然而，大多数岩石类材料的强度包络线是非线性的。在非线性准则中，HOEK等[3]提出的强度准则由于提供了可靠的工具预测岩体节理强度而被广泛认同，随后，HOEK−BROWN强度准则发展为广义形 式[4]，其中强度参数不再是常数，其取值从良好状态岩体的0.5到较差状态岩体的0.6，并被广泛应用。WANG等[5−8]对圆孔隧道开挖时的应力和变形弹塑性进行分析发现：理论分析方面，主要是基于理想弹塑、弹−脆性力学模型计算非关联流动法则下围岩应力、变形弹塑性解析表达式。许渊等[9]推导出考虑轴向力和渗透力共同作用下的弹−脆−塑性围岩的应力和位移非线性解。王水林等[10]通过将岩体应变软化过程简化为一系列脆塑性过程，基于经典弹塑性力学理论，提出了应变软化过程模拟方法及其相应的有限元求解过程。从国内外的研究特点可以看出，应变软化分析主要采用理论分析和数值模拟方法，理论分析可以在本质上反映应变软化状态，但在计算时参数大多是近似估算的，数值解比理论解有所降低，同时计算过程较复杂。为此，本文作者在以上理论分析的基础上，基于M−C强度准则，引入量纲一化方法进行精确求解，排除变量、参数在量纲上的影响，以期为软化围岩隧道的开挖设计与施工提供理论支持。

1 问题定义

图1所示为在无限均质岩体中开挖半径为的圆孔隧道，初始地应力0在开挖之前均布在隧道周围。当内在支撑力i低于临界值ic时，隧道周围会产生塑性破坏。对于弹脆塑或者理想弹塑性情况，可以推导出塑性区半径表达式[11−12]。若考虑应变软化情况，则可根据图1中的s处边界面将塑性区分为软化区和残余区，对这种情况一般无法求出闭合形式的解，同时塑性区和软化区的半径、应力分布和位移只能通过数值解进行估算。

图1 开孔过程中塑性区形成图

1.1 屈服函数

对于M−C屈服准则，有

1.2 塑性势函数

选用M−C准则作为塑性势函数，故塑性势函数可以表示为

1.3 强度参数演化

其中：代表剪胀角、黏聚力及内摩擦角中的任意1个；为临界塑性应变偏差即残余区初始值，可通过实验得到；下标p和r分别表示材料参数的峰值和残余值。

1.4 临界支撑力

只有当内在支撑力i低于临界值ic时，圆孔周围塑性区才会形成。对于M−C准则岩土体，ic为

后，在弹塑性边界面上(见图1)，径向应力R等于ic，且R独立于半径，

2 应变软化近似值

2.1 预处理

假设塑性区被分成个圆环，塑性半径为p。第个圆环在半径分别为和之间，如图2所示。在弹塑性边界上，应力和应变分别为：

图2 塑性区分环图

2.2 应力和弹性应变增量

本文采用一种新的量纲一化计算方法，将圆形隧道简化为轴对称模型，将开挖过程中应变软化围岩中塑性区按应力分成有限个满足平衡方程和几何相容方程的同心圆环，基于M−C强度准则，求解每环的平衡方程和相容方程得到应力应变增量，从而得出软化区应力和径向位移解。用量纲一化变量将物理平面 (，)转化成以为坐标系的单位面(其中，为半径，为塑性区半径与隧道半径比值)，变换式为[6, 13]：

转化的塑性区在单位半径的圆内，由变换式定义的空间被称为单位面。在单位平面上，弹塑性交界面被固定在=1处，而孔壁位于=1/处[14−15]。

对于M−C强度准则，根据式(2)和式(3)，令

内压力和外压力分别转化为

屈服条件改写为

根据CARRANZA-TORRES[4]提出的量纲一化方法，在变量的单位平面上，将式(14)或式(15)进行量纲一处理：

根据BROWN等[1]提出的方法，将软化区应力分成份，同时注意到塑性区从外部边界=p处的b到内部边界=处的i，应力增量可以转化为

故第个圆环应力可以近似求解为

式(19)中假设每一环应力增量为常量，而每一环的实际厚度取决于平衡方程。若足够大，则相应的环向应力为

2.3 位移近似解

上述方法将应力分成份，当足够大时，假设每一环岩体参数不变，根据量纲一化平衡方程可以表示为

第环的应力平衡方程可以近似为

而量纲一化的应变为

塑性区总应变是由弹性部分和塑性区部分组成，可以写成下列形式[16−17]：

相容方程又可以表示为

根据胡克定律，在平面应变条件下应变与应力的关系为

结合式(23)，(27)和(28)，可知

则第个圆环的总应力为

由于

其中：u为径向位移；为量纲一化径向位移。故量纲一化环向应变计量纲一化位移为：

将上述计算方法重复次求出结果，则塑性区半径为

3 算例验证

3.1 理论解可靠性验证

选取SHARAN[8]得出的应力与位移精确解进行对比，同时采用HOEK−BROWN(H−B)和M−C强度参数转换技术，对同一种岩体参数的理论解进行对比。参照SHARAN[8]的精确解参数，设定相同的输入参数：隧道半径=5 m，初始地应力0=30 MPa，围岩支护力i=5 MPa，围岩弹性模量=5 GPa，围岩泊松比=0.25，围岩单轴抗压强度峰值和残余值cp=cr=30 MPa，采用H−B强度参数与M−C强度参数进行转换的技术[13, 18]，获得的M−C强度参数p=2.146 78 MPa，p=26.364 5°，r=01.724 92 MPa，p=22.497 7°。基于M−C准则解的结果如图3和图4所示。

图3 量纲一化弹脆塑应力与精确应力转化解对比

图4 量纲一化弹脆塑位移与精确位移转化解对比

从图3可以看出：基于M−C强度准则解的应力分布情况符合软化分布规律，塑性区的径向和环向应力分布解均与精确解较吻合；当=0时，围岩为弹脆塑材料，由于不存在围岩软化区，在塑性区和弹性区交界面上，环向应力存在突变。图4所示为基于M−C强度准则的量纲一化弹−脆−塑位移与精确位移对比结果。从图4可以看出：基于M−C强度准则方法求得的位移比精确解略小，整体上误差满足要求。从计算效率看，本文量纲一化逐步应力法的计算时间为0.003 562 s，SHARAN[8]的计算时间为0.000 024 s。虽然本文计算效率比SHARAN[8]的计算效率低，但在本文计算中，由于两者计算时间都极短，本文的逐步应变方法考虑了围岩软化过程，故具有一定的理论 意义。

在应变软化特性分析中，为求得应力和位移，只对计算结果有较大影响的参数进行分析。选取分别为0，0.004，0.008，0.012和100，并选取100对M−C强度准则的解进行分析。其中=0时代表弹脆塑状态，=100时可以近似认为弹塑性状态，其他值代表软化状态。参照文献[4]设置计算参数：隧道半径=2 m，初始地应力0=15 MPa，围岩支护力i=25 MPa，围岩弹性模量=5.7 GPa，围岩泊松比=0.3，围岩单轴抗压强度峰值和残余值cp=cr=30 MPa，采用H−B强度参数与M−C强度参数进行转换的技术，获得的M−C强度参数p=1.781 46 MPa，p=26.869°，r=1.070 76 MPa，p=21.110 5°，计算结果如图5和图6所示。

图5 径向和环向应力随变化分布

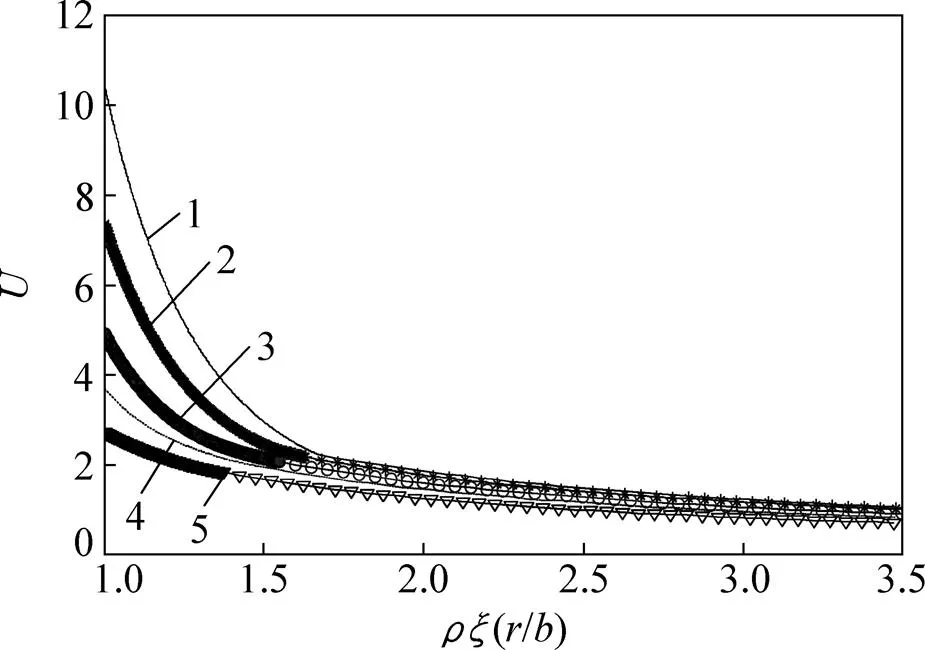
图6 量纲一化位移随变化分布

4 结论

1) 本文解的应力分布情况符合软化分布规律，塑性区的径向和环向应力及位移分布与精确解较吻合，证明了本文逐步应力量纲一化解的正确性和有效性。

[1] BROWN E T, BRAY J W, LADANYI B, et al. Ground response curves for rock tunnels[J]. Journal of Geotechnical Engineering, 1983, 109(1): 15−39.

[2] ALONSO E, ALEJANO L R, VARAS F, et al. Ground response curves for rock masses exhibiting strain-softening behaviour[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2003, 27(13): 1153−1185.

[3] HOEK E, CARRANZA-TORRES C, CORKUM B. Hoek−Brown failure criterion-2002 edition[C]//Proceedings of the 5th North American Rock Mechanics Symposium. Toronto, Canada, 2001: 267−273.

[4] CARRANZA−TORRES C, FAIRHURST C. The elasto-plastic response of underground excavations in rock masses that satisfy the Hoek−Brown failure criterion[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(6): 777−809.

[5] WANG Yang. Ground response of circular tunnel in poorly consolidated rock[J]. Journal of Geotechnical Engineering, 1996, 122(9): 703−708.

[6] PARK K H, KIM Y J. Analytical solution for a circular opening in an elastic-brittle-plastic rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(4): 616−622.

[7] PARK K H, TONTAVANICH B, LEE J G. A simple procedure for ground response curve of circular tunnel in elastic-strain softening rock masses[J]. Tunnelling and Underground Space Technology, 2008, 23(2): 151−159.

[8] SHARAN S K. Analytical solutions for stresses and displacements around a circular opening in a generalized Hoek–Brown rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(1): 78−85.

[9] 许渊, 李亮, 邹金锋, 等. 考虑轴向力和渗透力时圆形隧道广义Hoek-Brown解[J]. 岩土力学, 2015, 36(10): 2837−2846.
XU Yuan, LI Liang, ZOU Jingfeng, et al. Generalized Hoek-Brown solution of circular tunnel considering the effect of the out-of-plane stress and seepage force[J]. Chinese Journal of Rock Mechanics, 2015, 36(10): 2837−2846.

[10] 王水林, 郑宏, 刘泉声, 等. 应变软化岩体分析原理及其应用[J]. 岩土力学, 2014, 35(3): 609−622.
WANG Shuilin, ZHENG Hong, LIU Quansheng, et al. Analysis principle and application of strain softening rock mass[J]. Chinese Journal of Rock Mechanics, 2014, 35(3): 609−622.

[11] 李宗利, 任青文, 王亚红. 考虑渗流场影响深埋圆形隧洞的弹塑性解[J]. 岩石力学与工程学报, 2004, 23(8): 1291−1295.
LI Zongli, REN Qingwen, WANG Yahong. Elasto-plastic analytical solution of deep-buried circle tunnel considering fluid flow field[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(8): 1291−1295.

[12] LEE Y K, PIETRUSZCZAK S. A new numerical procedure for elasto-plastic analysis of a circular opening excavated in a strain-softening rock mass[J]. Tunnelling and Underground Space Technology, 2008, 23(5): 588−599.

[13] FAHIMIFAR A, MOHAMMAD R Z. A new closed-form solution for analysis of unlined pressure tunnels under seepage forces[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(11): 1591−1613.

[14] YANG Xiaoli, PAN Qiujin. Three dimensional seismic and static stability of rock slopes[J]. Geomechanics and Engineering, 2015, 8(1): 97−111.

[15] YANG Xiaoli, YIN Jianhua. Slope equivalent Mohr-Coulomb strength parameters for rock masses satisfying the Hoek-Brown criterion[J]. Rock Mechanics and Rock Engineering, 2010, 39(4): 505−511.

[16] WANG Shuilin, ZHENG Hang, LI Chunguan, et al. A finite element implementation of strain-softening rock mass[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(1): 67−76.

[17] WANG Shuilin, YIN Shunde, WU Zhenjun. Strain-softening analysis of a spherical cavity[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2012, 36(2): 182−202.

[18] 朱合华, 张琦, 章连洋. Hoek-Brown 强度准则研究进展与应用综述[J]. 岩石力学与工程学报, 2013, 32(10): 1945−1963.
ZHU Hehua, ZHANG Qi, ZHANG Lianyang. Review of research progresses and applications of Hoek-Brown strength criterion[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(10): 1945−1963.

(编辑 陈灿华)

Dimensionless analysis of stress numerical stepwiseprocedure in strain-softening rock mass

JIANG Wujun1, ZOU Jinfeng2

(1. Hunan Provincial Expressway Administration Bureau of Hunan Province, Changsha 410001, China;2. School of Civil Engineering, Central South University, Changsha 410075, China)

Based on generalized Mohr−Coulomb failure criterion, an improved numerical method and stepwise procedure for the stress and displacement analysis of a circular opening excavated in a strain-softening rock mass were proposed by using the dimensionless analysis method. By deviding the plastic region of strain-softening rocks into finite annuli and calculating the stress and strain increments, the stress and displacement in the plastic region were obtained. The stress and displacement increments of the annulus were obtained through the stress equilibrium and compatibility equation of the annulus, and the stress and displacement of strain-softening region were obtained. The validity and reliability of the proposed solution were confirmed by the existing theoretical solution. The influence of partial parameters on the stress and displacement was revealed by numerical calculation and parameter analysis. The results show that the dimensionless solution is in agreement with the exact solution when the number of the annulus is enough. The plastic region decreases with the increase of the critical plastic strain deviation, and the plastic residual area vanishes when the critical plastic strain deviation increases to a certain definite value. The plastic radius and displacement increase with the decrease of the critical plastic strain deviation. The softened region turns into brittle when the softening control parameter is equal to zero.

strain-softening; numerical stepwise stress procedure; Mohr−Coulomb failure criterion; circular tunnel

10.11817/j.issn.1672-7207.2016.08.040

TU921

A

1672−7207(2016)08−2842−06

2016−01−11；

2016−03−03

国家自然科学基金资助项目(51208523)(Project (51208523) supported by the National Natural Science Foundation of China)

邹金锋，博士，副教授，从事岩土与地下工程的研究；E-mail：zoujinfeng_csu@163.com