扁率摄动对地球同步轨道SAR成像聚焦的影响分析

胡文龙

①（中国科学院电子学研究所 北京 100190）

②（中国科学院空间数据处理与应用系统技术重点实验室 北京 100190）

扁率摄动对地球同步轨道SAR成像聚焦的影响分析

胡文龙*①②

①（中国科学院电子学研究所 北京 100190）

②（中国科学院空间数据处理与应用系统技术重点实验室 北京 100190）

针对地球同步轨道星载合成孔径雷达（Geosynchronous Synthetic Aperture Radar，GEOSAR）长合成孔径成像受地球扁率摄动影响的问题，推导了卫星不同轨道根数受摄动所导致的雷达回波多普勒调频率和2次相位公式，通过分析扁率摄动对成像的影响，得到结论：地球扁率摄动使雷达回波产生附加的2次相位调制，相位调制的主导成分是卫星轨道长半轴受摄分量，相位调制幅度与成像所采用的轨道弧段有关，2次相位调制总量经过分钟量级的长合成孔径累积几乎在卫星运动全周期超过45°的容限。雷达成像聚焦不能简单忽略扁率摄动的影响，必须采取相应的补偿措施，否则会造成图像散焦。

地球同步轨道SAR；轨道摄动；SAR成像

引用格式：胡文龙.扁率摄动对地球同步轨道SAR成像聚焦的影响分析［J］.雷达学报，2016，5（3）：312-319.DOI：10.12000/JR15121.

Reference format：Hu Wenlong.Impact of Earth's oblateness perturbations on geosynchronous SAR data focusing［J］.Journal of Radars，2016，5（3）：312-319.DOI：10.12000/JR15121.

1　引言

地球同步轨道SAR（Geosynchronous Synthetic Aperture Radar，GEOSAR）是以地球同步卫星为平台的成像雷达。GEOSAR“站得高、看得远”，具有重访周期短、可视范围大等优点，可以克服现行低轨星载SAR的一些缺点。GEOSAR的概念是30多年前提出的［1，2］，近年来作为星载SAR的一个前沿研究方向受到关注，并有一批文献发表，涉及到GEOSAR的主要研究内容，如应用概念［3-5］、系统体制［6，7］、分辨率分析［8-10］、成像方法［11-14］、信号传播扰动补偿［15-18］等。

与传统的低轨星载SAR相比较，GEOSAR成像最根本的特点是合成孔径时间长。典型的大倾角、圆轨道GEOSAR采用正侧视成像模式，合成孔径时间可以达到约5 min的量级。若利用GEOSAR与地球的同步运动特性、再配合以2维天线波束指向控制，可以形成类似于光学“凝视”成像的观测模式，实现雷达对目标定点、持续性驻留成像观测，成像合成孔径时间则更长。

长合成孔径这一根本特点使得GEOSAR面临许多新问题，其中之一就是长合成孔径条件下卫星轨道摄动对成像的影响。目前的GEOSAR研究文献大多不涉及轨道摄动对成像影响的问题。少数文献如文献［19］面向大倾角、圆轨道GEOSAR卫星，针对轨道摄动使雷达回波产生附加的多普勒调制的影响途径，采用数值方法分析了地球非球形摄动、三体引力摄动和太阳光压摄动短周期项对成像的影响，给出3种轨道摄动对成像聚焦有影响的整体结论，但其分析过程局限于所采用的数值方法尚缺乏对各种摄动因素的深入分析。

本文在文献［19］工作的基础上，针对3种摄动之一的地球非球形引力中的扁率摄动，从GEOSAR星地几何特性和卫星轨道摄动原理出发提出近似分析方法，通过推导GEOSAR轨道根数受摄动所导致的雷达回波多普勒调频率和2次相位公式，对扁率摄动对GEOSAR成像聚焦的影响进行进一步分析。

2　星地几何关系

GEOSAR卫星采用什么样的轨道，是一个有待深入研究的问题。但由卫星轨道动力学特性可知，在各种轨道的地球同步卫星之中，采用了大倾角、星下点轨迹为“8字形”的圆轨道卫星的运动速度和高度变化较小，多普勒带宽较大，有利于星载SAR的成像处理和应用。故与大多数GEOSAR文献一样，本文以大倾角、圆轨道的地球同步卫星作为分析对象。

为进行GEOSAR受地球扁率摄动影响的受摄分析，首先需要给出星地几何关系的描述。低轨星载SAR文献经常对成像过程所涉及的地球局部采用球模型近似［20］。本文考虑到GEOSAR卫星轨道远高于低轨SAR这一更为有利的条件，也以球模型作为地球的整体近似。

考虑卫星星下点在地球表面的运动关系。在卫星圆轨道、地球球模型条件下，由卫星轨道面、地球赤道面和卫星星下点所处的子午面分别与地球球面相交，构成一个球面三角形NDS如图1所示。

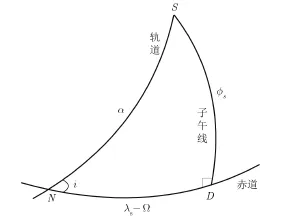
图1　GEOSAR星下点在地球表面构成的球面三角形Fig.1 Spherical triangle of GEOSAR nadirs on the Earth's surface

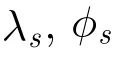
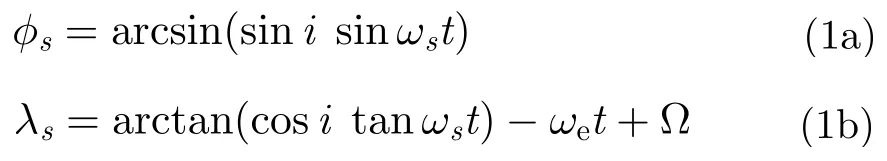
顺便指出，上述星下点经纬度指的是地心经纬度。在地球球模型假设条件下，地心经纬度与常用的大地经纬度相等。

GEOSAR星地几何关系则由图2给出。其中，a为卫星轨道长半轴，Re为地球半径，β为目标T和卫星星下点S对地心的张角，γ为卫星下视角。

本文主要考虑GEOSAR对地面目标的定点观测即“凝视”成像，即无论卫星在成像过程之中运动到什么轨道位置，雷达天线通过波束扫描控制始终指向卫星视场之内的观测目标。若T为卫星视场之内的某地球表面固定成像目标，卫星与目标之间的距离即斜距为R，则由图2的几何关系可以得到：

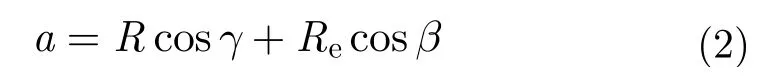
由于GEOSAR轨道很高，根据星地关系容易计算出γ＜8.7。，即cosγ＞0.9885，故本文取近似cosγ≈1，于是有

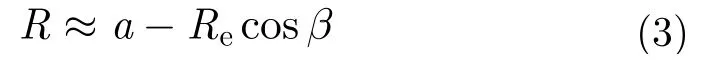
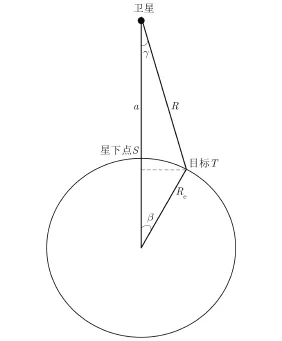
图2　GEOSAR卫星与地面目标构成的星地几何关系Fig.2 GEOSAR imaging geometry

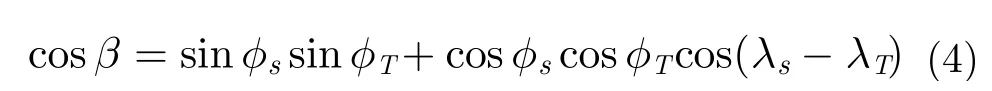
将式（4）代入式（3）得到目标斜距方程为：

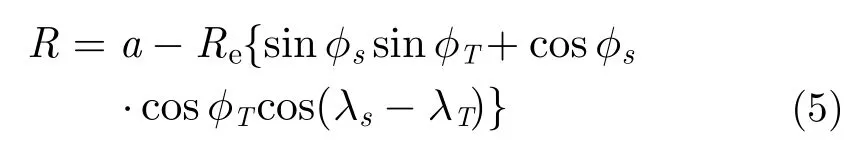
注意到本文所得到的目标斜距解析表达式（5）是在地球球模型假设和取近似cosγ≈1的条件下取得的。实际上，地球不是一个理想的球体，地球赤道半径为6378.139 km、极半径为6356.733 km。采用球模型近似之后，图2地心三角形目标位置处的地球半径误差也会投影到斜距方向上形成的斜距误差。但考虑到目标位置在成像过程中固定不变，该误差是一个不随时间变化的固定误差，不影响本文所讨论的成像聚焦问题。此外，由于GEOSAR轨道很高，对于处于卫星视场之内的任何目标，下视角γ很小且合成孔径之内近似不变，由cosγ≈1近似导致的也是不超过1-0.9885=1.5％的固定误差，不影响成像聚焦。

3　雷达受摄多普勒调频率

根据上一节星地几何关系，本文所采用的扁率摄动近似分析方法是：以式（1）、式（5）作为二体无摄动条件下的卫星运动解和目标斜距解，将式（1）、式（5）中的轨道根数a，Ω，i看作常数，将卫星受摄看成是对二体运动的附加调制，使得a，Ω，i产生了附加的时间变化率。分析方法首先由拉格朗日摄动方程求得该附加的时间变化率，然后求得摄动导致的斜距变化率和雷达回波多普勒频率。

GEOSAR卫星是地球同步轨道卫星的一种，卫星主要摄动包括地球非球形摄动、日月三体摄动和太阳光压摄动。本文目的在于分析地球非球形摄动的带谐主项J2即地球扁率摄动的影响。J2摄动反映了地球两极扁、赤道凸的形状特征，故称扁率摄动。在影响GEOSAR的3种主要摄动力中，地球非球形摄动力高于日月三体摄动和太阳光压摄动1个数量级，而J2项又高于地球非球形摄动其他主项3个数量级［22］，故J2项是GEOSAR成像聚焦所需要考虑的最主要摄动因素。

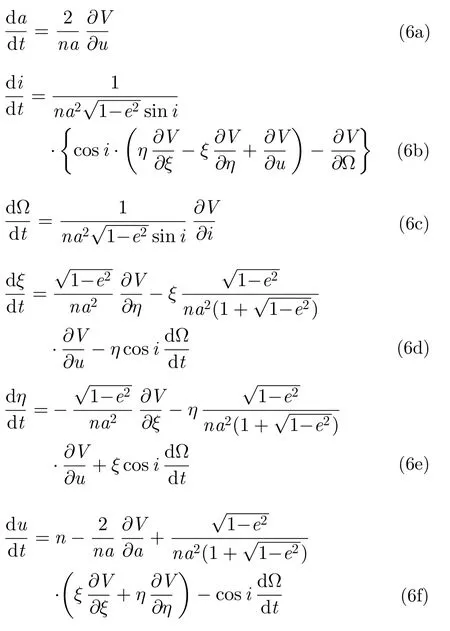
对于地球扁率摄动J2，其位函数为［22］：

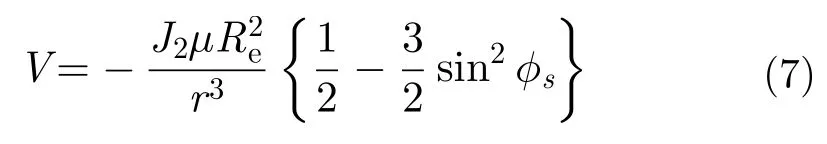
其中，φs是星下点经纬度，J2为带谐系数，μ为地球引力常数，r为卫星地心距，Re是摄动力模型中的地球半径。由式（1）sin φs=sini sinωst，同时取圆轨道GEOSAR地心距r等于长半轴a，则式（7）变为：

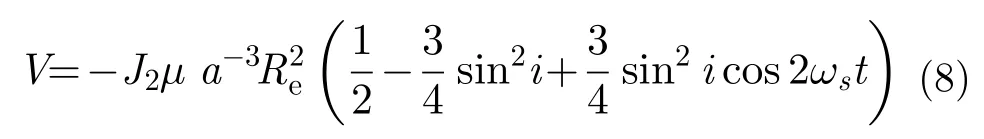
于是，根据式（8）求出J2位函数关于根数的偏导数，再代入式（6）即可求得卫星轨道根数受摄变化率。

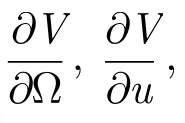
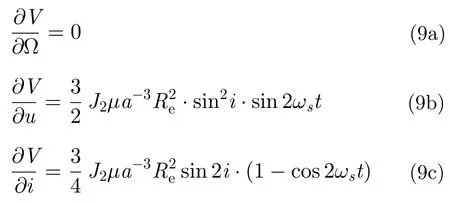
再代入（6）即得GEOSAR部分轨道根数因受摄所导致的时间变化率分别为：

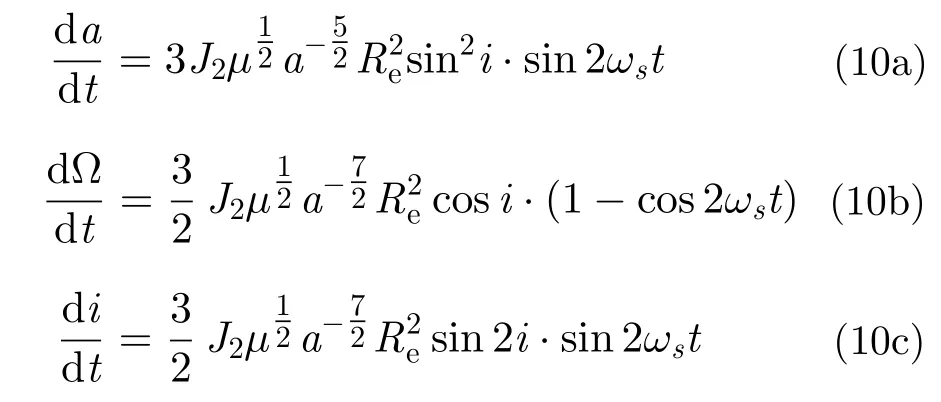
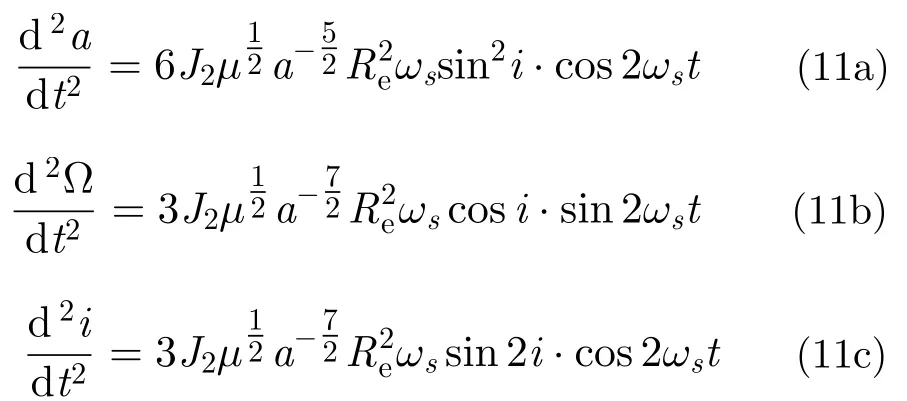
在得到卫星轨道根数受摄的1阶、2阶导数之后，就可以利用目标斜距依赖于轨道根数的函数关系式（5），将摄动影响引入斜距表达式，进而求得雷达受摄多普勒调频率。由于目标斜距依赖a，Ω ，i等轨道根数，于是目标斜距因摄动导致的1阶变化率为：

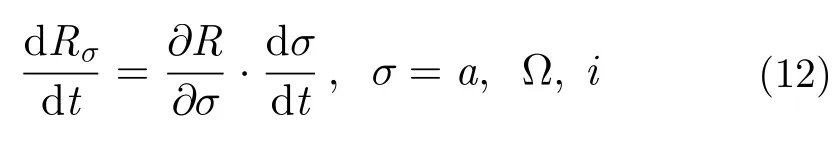
式中用σ统一表示各卫星轨道根数，省略推导过程，根据式（1）、式（5）可得目标斜距关于σ的偏导数为：

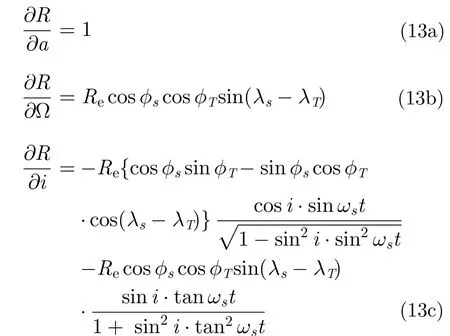
由式（12）可得目标斜距因各轨道根数受J2摄动的2阶变化率为：

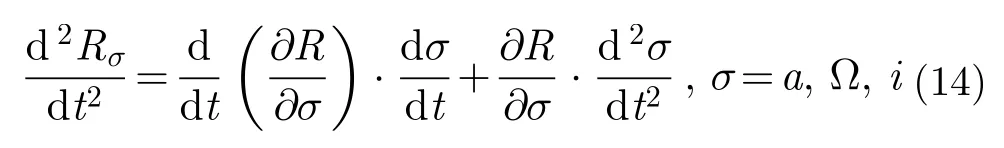
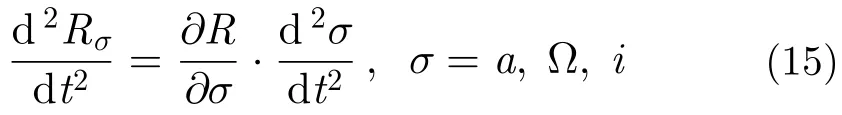
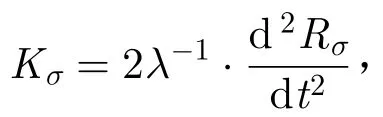
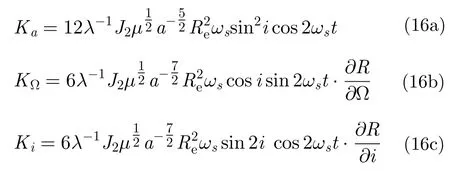
需要强调的是，上述结果不包括卫星因二体运动所产生的多普勒调频率，只是J2摄动产生的附加多普勒调频率。

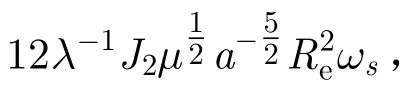
4　雷达成像聚焦受摄分析

为分析GEOSAR长合成孔径成像聚焦受摄问题，本文称成像合成孔径时间所对应的卫星轨道运动区间为成像弧段，定义合成孔径起点为合成孔径参考点。这有别于低轨星载SAR文献通常采用合成孔径中点为合成孔径参考点，原因也在于GEOSAR长合成孔径“凝视”成像中，斜距历程不再具有关于合成孔径中点对称的抛物线特性。

根据SAR成像理论［23，24］可知，SAR成像聚焦必须采用精确反映雷达和目标相对运动关系的多普勒参数构造匹配滤波器。其中，多普勒调频率是影响成像聚焦的关键参数，多普勒调频率不准确导致成像散焦。由以上分析可知，J2摄动等效于给雷达回波附加了一个多普勒调频率。合成孔径成像过程必须考虑这一多普勒调频率所形成的2次相位积累量是否超出0.25π容限。

首先分析长半轴受摄的情况。由式（16a）得长半轴受摄2次相位积累总量为：

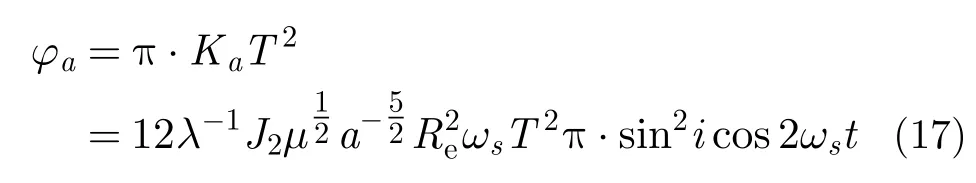
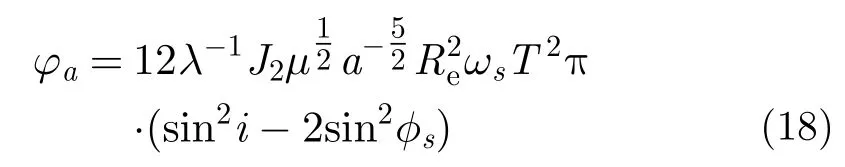
可见，卫星因长半轴受摄2次相位具有非常简洁的表达式，仅成像弧段纬度有关，与成像弧段经度和目标位置都无关。与纬度有关、与经度无关正说明了J2摄动反映的是地球赤道凸、两极扁的扁状特征。此外，与目标位置无关是因为GEOSAR轨道高、对地下视张角小，采用cosγ≈1进行星地几何关系近似分析的结果，且由上一节的结论知这一近似不影响GEOSAR成像聚焦的受摄分析。

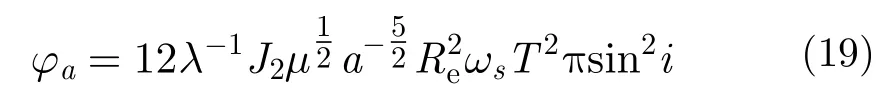
在

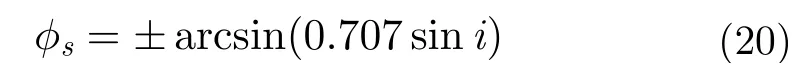
处取最小值0。若式（18）左端取为受摄2次相位的容限值0.25π，容易得到2次相位取0.25π时的卫星纬度为：

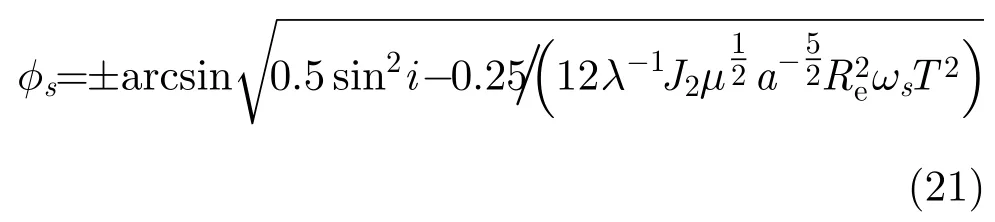
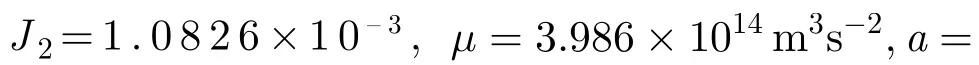
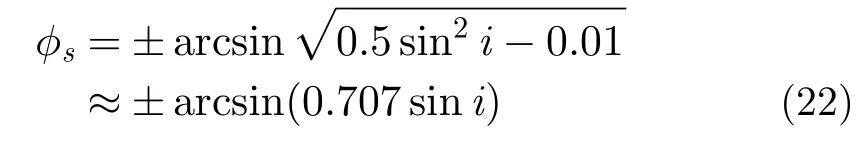
由此即可以得出结论，GEOSAR仅仅因为长半轴受J2摄动所导致的附加2次相位，经过5 min合成孔径积累就超出了0.25π，而且这种影响几乎遍及卫星轨道运动的全周期。因而，GEOSAR成像不能简单地忽略这一附加相位，否则将造成很大的2次相位误差，使成像散焦。此外，成像有利的赤道附近弧段受摄影响最大。赤道附近轨道弧段之所以对成像有利原因在于：卫星在赤道附近运动速度大、多普勒带宽大；我国为北半球国家，我国SAR成像目标主要位于北半球中低纬度，卫星处于赤道附近轨道时，星地几何关系更接近SAR成像理论所要求的正侧视模式，成像处理难度相对较小。

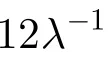
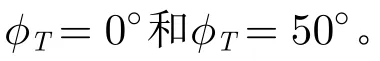
利用数值计算给出的各种受摄2次相位随成像弧段纬度变化的曲线如图3所示。

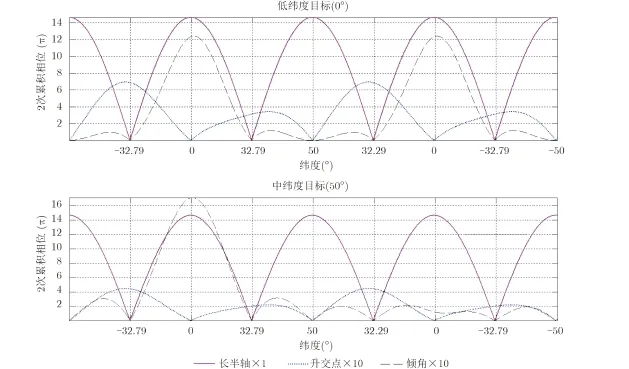
图3　GEOSAR轨道根数受摄2次累积相位随纬度变化的曲线Fig.3 Illustration of the accumulating quadratic phases at different latitudes caused by orbital perturbation from the Earth's oblatenes

为了将升交点、倾角受摄与长半轴进行比较，图3也画出了长半轴受摄的数值曲线。由于长半轴受摄较大，故图3中卫星轨道升交点和倾角受摄2次相位量级被放大了10倍，以便3条曲线能够在统一的坐标尺度下加以比较。

图3的数值分析结果表明，成像弧段选取在不同的轨道位置，雷达受摄影响是不同的。其中，长半轴受摄在几乎全部弧段都超出0.25π门限，这与前面的解析分析结果一致。其他轨道根数受摄情况较为复杂，但在全轨道周期内都存在超出0.25π的弧段。纬度不同目标相比较，低纬度目标总体上所受影响略大。

以上分析是以L波段和5 min合成孔径时间为例的。实际上，GEOSAR对地定点成像应用在绝大多数情况下所需要的合成孔径时间都超过5 min，显然合成孔径时间越长成像受影响越严重；此外，L波段也是GEOSAR所允许采用的较长工作波段，由于雷达受摄附加相位与雷达工作波长成反比，同样，GEOSAR工作频率越高，受摄动影响也越严重。

5　结论

本文针对圆轨道GEOSAR推导了卫星轨道根数受地球扁率摄动所导致的雷达回波多普勒调频率和2次相位公式，分析了地球扁率摄动对GEOSAR成像聚焦的影响，得出结论：地球扁率对卫星轨道长半轴摄动高于其他轨道根数1个数量级以上，是卫星受摄影响的主要成分；GEOSAR成像聚焦过程几乎在全轨道弧段受到扁率摄动的严重影响，必须采取相应措施补偿扁率摄动的影响，否则会造成图像的严重散焦。

致谢感谢西安卫星测控中心王家松研究员对本文所给出的意见。

［1］Tomiyasu K.Synthetic aperture radar in geosynchronous orbit［C］.IEEE Antennas and Propagation Sympsium，Maryland，USA，1978：42-45.

［2］Tomiyasu K and Pacell J L.Synthetic aperture radar imaging from an inclined geosynchronous orbit［J］.IEEE Transactions on Geoscience and Remote Sensing，1983，21（3）：324-329.

［3］Madsen S N，Edelstein W，DiDomenico L D，et al..A geosynchronous synthetic aperture radar； for tectonic mapping，disaster management and measurements of vegetation and soil moisture［C］.Proceedings of IEEE Geoscience and Remote Sensing Symposium（IGARSS），Sydney，2001：447-449.

［4］Davide B，Hobbs S E，and Giuseppe O.Geosynchronous synthetic aperture radar：concept design，properties and possible applications［J］.Acta Astronautica，2006，59（1/5）：149-156.

［5］朱敏慧.地球同步轨道星载合成孔径雷达概念研究［J］.现代雷达，2011，33（5）：1-4.Zhu Min-hui.The concepts about geosynchronous synthetic aperture radar［J］.Modern Radar，2011，33（5）：1-4.

［6］Ruiz-Rodon J，Broquetas A，Makhoul E，et al..Nearly zero inclination geosynchronous SAR mission analysis with long integration time for earth observation［J］.IEEE Transactions on Geoscience and Remote Sensing，2014，52（10）：6379-6391.

［7］Hobbs S，Mitchell C，Forte B，et al..System design for geosynchronous synthetic aperture radar missions［J］.IEEE Transactions on Geoscience and Remote Sensing，2014，52（12）：7750-7763.

［8］Wu Z，Huang L，Hu D，et al..Azimuth resolution analysis in geosynchronous SAR with azimuth variance property［J］.Electronics Letters，2014，50（6）：464-466.

［9］Hu C，Zeng T，Zhu Y，et al..The accurate resolution analysis in Geosynchronous SAR［C］.2010 8th European Conference on Synthetic Aperture Radar，Aachen，2010：1-4.

［10］Wu Z，Huang L，Hu D，et al..Ground resolution analysis based on gradient method in geosynchronous SAR［C］.2013 IEEE International Conference on Signal Processing，Communication and Computing，Kunming，2013：1-4.

［11］Bruno D，Hobbs S E，et al..Radar imaging from geosynchronous orbit：temporal decorrelation aspects［J］.IEEE Transactions on Geoscience and Remote Sensing，2010，48（7）：2924-2929.

［12］Hu C，Long T，Zeng T，et al..The accurate focusing and resolution analysis method in geosynchronous SAR［J］.IEEE Transactions on Geoscience and Remote Sensing，2011，49（10）：3548-3563.

［13］Zhao B，Qi X，Song H，et al..An accurate range model based on the fourth-order Doppler parameters for geosynchronous SAR［J］.IEEE Geoscience and Remote Sensing Letters，2014，11（1）：205-209.

［14］Hu C，Long T，Liu Z，et al..An improved frequency domain focusing method in geosynchronous SAR［J］.IEEE Transactions on Geoscience and Remote Sensing，2014，52（9）：5514-5528.

［15］Tian Y，Hu C，Dong X，et al..Theoretical analysis and verification of time variation of background ionosphere on geosynchronous SAR imaging［J］.IEEE Geoscience and Remote Sensing Letters，2015，12（4）：721-725.

［16］Wadge G，Guarnie A M，Hobbs S E，et al..Potential atmospheric and terrestrial aplications of a geosynchronous radar［C］.2014 IEEE Geoscience and Remote Sensing Symposium（IGARSS），Quebec，2014：946-949.

［17］Ruiz Rodon J，Broquetas A，Guarnieri A，et al..Geosynchronous SAR focusing with atmospheric phasescreen retrieval and compensation［J］.IEEE Transactions on Geoscience and Remote Sensing，2013，51（8）：4397-4404.

［18］Kou L，Xiang M，Wang X，et al..Tropospheric effects on L-band geosynchronous circular SAR imaging［J］.IET Radar，Sonar & Navigation，2013，7（6）：693-701.

［19］Jiang Mian，Hu Wen-long，and Ding Chi-biao.The effects of orbital perturbation on geosynchronous synthetic aperture radar imaging［J］.IEEE Geoscience and Remote Sensing Letters，2015，12（5）：1106-1110.

［20］Li F and Johnson W T K.Ambiguities in spaceborne synthetic aperture radar systems［J］.IEEE Transactions on Aerospace and Electronic Systems，1983，19（3）：389-396.

［21］陈芳允.卫星测控手册［M］.北京：科学出版社，1992：110-137.Chen Fang-yun.A Handbook for Satellite Measurement and Control［M］.Beijing：Science Press，1992：110-137.

［22］刘林.人造地球卫星轨道力学［M］.北京：高等教育出版社，1992：91-193.Liu Lin.Orbital Mechanics of Artificial Satellites［M］.Beijing：Higher Education Press，1992：91-193.

［23］Curlander J C and Mcdonough R N.Synthetic Aperture Radar System and Signal Processing［M］.New York：John Wiley & Sons Inc.，1991：155-207.

［24］Cumming I G and Won F H.Digital Processing of Synthetic Aperture Radar Data：Algorithms and Implementation［M］.Norwood MA：Artech House Inc.，2005：567-584.

胡文龙（1963-），男，籍贯安徽，北京航空航天大学博士学位，中国科学院电子学研究所研究员。主要研究方向为雷达信号处理、雷达目标识别、高轨SAR新体制新方法等。

E-mail：wlhu@mail.ie.ac.cn

Impact of Earth's Oblateness Perturbations on Geosynchronous SAR Data Focusing

Hu Wenlong①②

①（Institute of Electronics，Chinese Academy of Sicences，Beijing 100190，China）

②（Key Laboratory of Technology in GeoSpatial Information Processing and Application System，Chinese Academy of Sicences，Beijing 100190，China）

In this study，we focus on the ultra-long integration of orbital perturbations of geosynchronous Synthetic Aperture Radar（SAR）for imaging.By deriving mathematical expressions for the Doppler rate and quadratic phase from orbital elements perturbated by oblateness or the J2 term of the non-spherical gravitational force of the Earth，we analyze the impact on SAR data focusing.Based on our results，we conclude that the quadratic phase will exceed 45°，which is the defocusing threshold for imaging，after accumulation during a long integration time at the minute level.Because the potential for defocusing exists throughout nearly the entire satellite motion cycle，the SAR processor must carefully manage and compensate for the quadratic phase to avoid image degradations.

Geosynchronous SAR（GEOSAR）； Orbital perturbation； SAR imaging

The National Ministries Foundation

TN959.74

A

2095-283X（2016）03-0312-08

10.12000/JR15121

2015-11-16；改回日期：2016-03-31；网络出版：2016-05-19

胡文龙 wlhu@mail.ie.ac.cn

国家部委基金