变式延伸，拓展讲评内容，提高试卷讲评效率

盛建武

试题由于受考试卷面、考试时间等的限制，试卷不可能涉及所学知识的全部。命题者往往以点带面来考查学生的数学知识与能力。在进行试卷讲评时，教师仅仅停留在知识点的层面上，就题论题，没有知识的归纳总结与拓展提升，缺乏知识的系统性。学生的收获是只会解一道题，不能旁通一类题，显然这种就题论题的讲评是不可取的。

讲评课涉及的内容都是学生已学过的知识，但评讲内容决不应是原有形式的简单重复，必须有所变化和创新。在设计讲评方案时，对于同一知识点应多层次、多方位加以解剖分析，同时注意对所学知识进行归纳总结、提炼升华，以崭新的面貌展示给学生，在掌握常规思路和解法的基础上，启发新思路，探索巧解、速解和一题多解，让学生感到内容新颖，学有所思，思有所得。通过讲评，训练学生由正向思维向逆向思维、发散思维过渡，提高分析、综合和灵活运用能力。同时，针对试卷中具有较大灵活性和剖析余地的典型试题要作进一步“借题发挥”，引起学生思维的发散，开拓思考的视野，从而促进其创新素质的提高。

一、一题多解：训练学生思维的灵活性

对于试题中的典型题目，教师应把学生的解题途径作为素材提炼、扩充、变通，使学生多方位、多角度地掌握解题的途径，从中顿悟出题目的本质来，增强解题悟性，激发学生思维。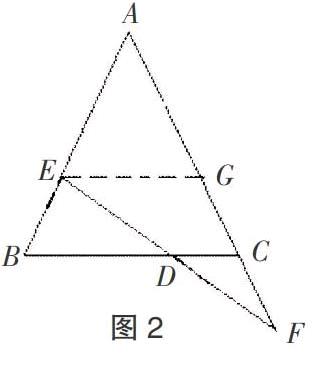

案例1： 已知：在△ABC中，AB=AC，E是AB上一点，F是AC延长线上一点，BE=CF，EF交BC于点D。求证：DE=DF。

这是一题典型的证明两线段相等的几何问题。在讲评时，我让学生自己来讲解解题思路，充分暴露学生的思维过程，使学生的思维应变能力得到充分的锻炼和培养。

生1：（利用平移法构造全等三角形证明）如图1，过点E作EG∥AF交BC于点G，得∠1=∠2=∠B，因此EB=EG=FC，由平行线的性质得∠3=∠4，∠5=∠6，所以△EGD≌△FCD，从而证得结论DE=DF；

生2：（利用三角形的中位线定理证明）如图2，过E点作EG∥BC交AC于点G，由∠B=∠ACB得到梯形EBCG为等腰梯形，而EB=CF，则GC=CF，因此CD为△FEG的中位线，从而证得结论DE=DF；

生3：（利用平行四边形的性质证明）如图3，过F作FG∥BA交BC延长线于点G，由∠1=∠2，∠1=∠3，∠2=∠4，得∠3=∠4，从而FC=FG，又已知FC=BE，得FG=BE，所以四边形BFGE为平行四边形，从而证得结论DE=DF；

生4：（利用相似三角形证明）如图4，过E作EG∥AF交BC于点G，得△EGD∽△FCD，又∠1=∠2=∠B，所以EB=EG=FC，即DE∶DF = EG∶FC = 1∶1，从而证得结论DE=DF。

以上四种证法分别用到了全等三角形的对应边相等、三角形的中位线定理、平行四边形的性质、相似三角形的性质等。体现了知识的纵向、横向的结合，辅助线的添设也各有特色，展示了证明两线段相等问题的一般规律。这样的讲评，不仅使学生真正掌握此类问题的解法，更重要的是训练了学生思维的灵活性与选择性。

二、一题多问：训练学生思维的广阔性

为提高讲评课的效果，教师应充分挖掘试题的深度与广度，扩大试题的辐射面，把分散的知识点串成一条线，形成知识链，以达到“解答一题，联通一片”目的。

案例2：如图5，已知点C是线段AB上的一点，△ACM，△BCN都是等边三角形。求证：AN=BM。

本题的证明不难，只需证△ACN≌△MCB即可。但在讲评时，我并没有到此为止，而是趁热打铁，充分挖掘试题的价值，让学生结合图形，深入探讨以下问题：

（1）图形中的全等三角形有几对？（△ACN≌△MCB，△ACD≌△MCE，△DCN≌△ECB）

（2）连结DE，猜想△CDE的形状；（△CDE是等边三角形）

（3）猜想DE与AB的位置关系；（DE∥AB）

（4）若AN与BM交于点O，求∠AOM的度数；（∠AOM = 60°）

（5）取AN的中点G，BM的中点H，连结CG，CH，GH，求证：△ACG≌△

MCH；

（6）猜想△CGH的形状；（△CGH是等边三角形）

（7）若将三角形△CBN绕点C按顺时针方向旋转角a（a为锐角）后，以上结论是否还成立？为什么？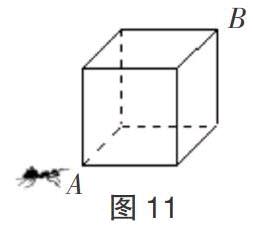

（8）若将图中的“等边三角形”改为“正方形”，以上探讨的结论还成立吗？（限于篇幅，问题（7）、（8）留给读者思考）

经过上述探讨、证明，涉及了更多的知识，从而使学生的思维在不断地深化，让学生及时弄懂未掌握的知识，并在消化过程中学到了新知识，培养探究创新能力。

三、一题多变：训练学生思维的变通性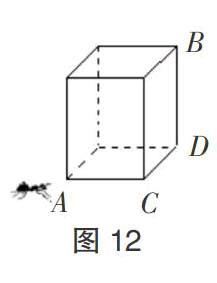

一题多变是变式教学的重要形式，它有助于学生抓住问题的本质，从中寻找他们之间的内在联系，探索出一般规律，从而提高学生的思维品质和应变能力。因此，试卷讲评时要通过原题目延伸出更多具有相关性、相似性、相反性的问题，加强知识的纵横联系，加大知识摄入量，实现“以少胜多”。

案例3： 如图6，在△ABC中，∠ABC、∠ACB的平分线相交于点P，若∠A = 60°，则∠BPC = °。

本题是一道有关三角形内角平分线知识的常规题型，并不是很难。但在讲评时，教师可借题发挥，延伸出更多相关的问题，让学生进行探索：

问题1：（将“两条内角平分线”改为“一条为内角平分线，另一条为外角平分线”）如图7，BP、CP分别是△ABC的内角平分线和外角平分线，若∠A= 60°，则∠BPC = °；

问题2：（将“两条内角平分线”改为“两条外角平分线”）如图8，BP、CP分别是△ABC的外角平分线，若∠A= 60°，则∠BPC= °；

问题4：（将“两条内角平分线”改为“两条高”）如图9，BD、CE是△ABC的两条高，相交于点P，试探讨∠BPC与∠A之间的关系。（∠BPC= 180°-∠A）

本题讲评对相关知识进行了有效的拓展与迁移，通过对该知识联系到的相似知识和相关的知识进行比较，鉴别和再认识，以培养学生举一反三，融会贯通的能力。

四、多题一解：训练学生思维的深刻性

通过多题一解让学生概括基本规律，可以培养学生求同存异的思维能力。许多数学习题看似不同，但他们的内在本质，或者说是解题的思路、方法是一致的，这就要求教师在试卷讲评中重视对这类题目的收集、比较，引导学生寻求通法、通解，并让学生感悟它们之间的内在联系，形成数学思想方法。

案例4：如图10，有一个圆柱，它的高为12厘米，底面半径为3厘米，在圆柱下底面的点A处有一只蚂蚁，它想吃到上底面与点A相对的点B处的食物，需要爬行的最短路程是 厘米。（π的值取3）

解此题应将圆柱侧面展开后，依据“两点之间线段最短”的性质，运用勾股定理求出线段AB的长即可。此类问题的解法还可以推广到正方体、长方体、台阶等情境中。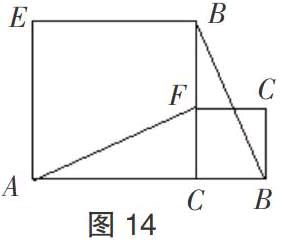

问题1：如图11，一只蚂蚁从点A出发，沿正方体表面爬行到点B处，若正方体的棱长为4厘米。则蚂蚁需要爬行的最短路程是 厘米。

问题2：如图12，在长方体中，AC = 3cm，CD = 5cm，DB =6cm，一只蚂蚁从点A出发，沿长方体表面爬行到点B处。则蚂蚁需要爬行的最短路程是 cm。

问题3：如图13是一个三级台阶，它的每一级台阶的长、宽、高分别是20dm、3dm、2dm，A和B是这个台阶的两个相对的端点，一只蚂蚁从点A出发，沿台阶表面爬行到点B处。则蚂蚁需要爬行的最短路程是 dm。

以上问题虽然思维方式有所不同，但本质是一致的，考查的都是转化思想（由立体转化成平面），运用的知识都是勾股定理，通过这样的讲评能使学生达到做一题，学一法，会一类的效果。

五、结论推广：训练学生思维的发展性

试卷讲评时，教师应充分挖掘试题的潜在功能，对一些重要的结论应不失时机地加以推广，以完善知识体系，拓展解决问题的思维空间。

案例5： 如图14，点C在线段AB上，分别以AC、BC为边在线段AB的同侧作正方形ACDE和CBGF，连接AF、BD，试问AF与BD有何关系？为什么？

本题通过证△ACF≌△DCB，可得AF=BD，AF⊥BD。但在试题讲评时，我没有就题论题，而是对所得的结论进行推广与拓展，以使学生深刻领会问题的本质，发展思维能力。

（1）如果点C在线段AB的延长线上，所得的结论是否成立？请画出图形，并说明理由。

（2）如果点C不在直线AB上时（点C在直线AB的上方或下方），AF与BD的关系是否仍然成立？

（3）若将图中的正方形CBGF绕点C旋转任意角度，AF与BD的上述关系是否还成立？

通过对图形进行一图多变的发散性变化，让学生在图形的变化过程中感受静与动，变与不变的辨证统一关系，让学生在体会数学奥妙的同时，提高自主探究的能力。

（作者单位：湖南省长沙市开福区教育科研培训中心）