解析几何核心完美突破
2016-09-30张红红
张红红
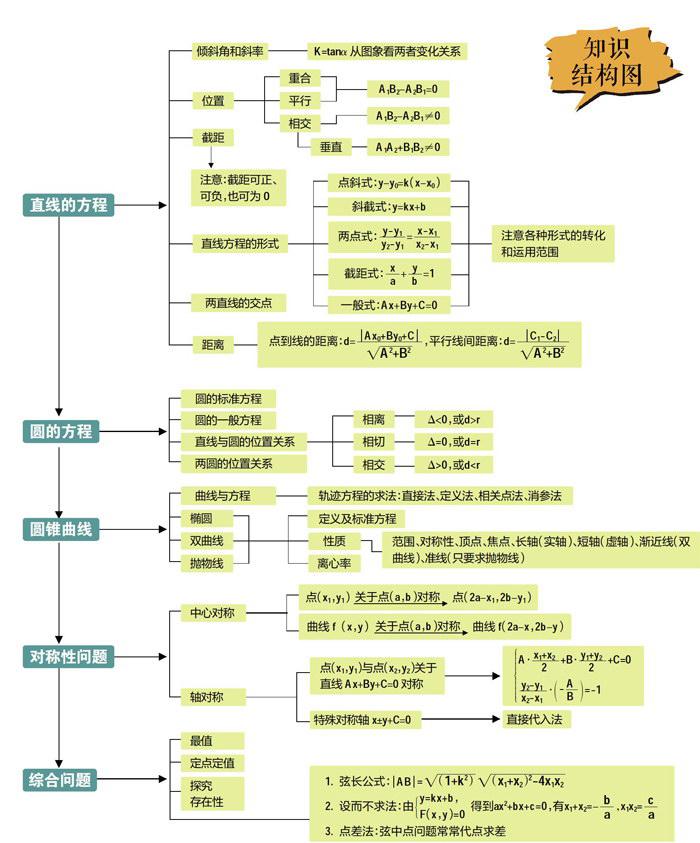


解析几何板块在高考中占有十分重要的地位,出题形式为:必做题中往往有一道或两道客观题(5或10分)和一道主观题(12至14分),选做题中的坐标系与参数方程(10分)后者的知识结构和方法应用实质上也属于解析几何,只是坐标系的选取和方程的表现形式发生了变化。
重要考点分布规律为:(1)圆、椭圆、双曲线和抛物线的定义、标准方程与图形的几何性质常常出现在客观题和主观题的第一小题,属于低、中档题;(2)与直线和圆锥曲线的位置关系相关的问题(如弦长、三角形面积、夹角等数量关系等)常常出现在主观题中的第二小题,属于难题由于考查重点和难点聚焦在最值、定点定值、探究存在性这些热点问题上,所以同学们的复习备考也是有章可循的。
考点1:直线和圆
名师圈点
在求过某点A(m,n)的圆的切线方程时,应先判断点与圆的位置关系,若点在圆上,切线有且只有一条;若点在圆外,切线必有两条,此时如果仅求得一条。则漏了斜率不存在的情况,即x=m,应补上。
考点2:圆锥曲线的定义、标准方程与图形的几何性质
命题点
(1)圆、椭圆、双曲线和抛物线的定义、标准方程与图形的几何性质;
(2)离心率的计算方法;
(3)焦半径的范围;
(4)轨迹方程的求法.
名师圈点
焦点三角形PFlF2中,常常想到圆锥曲线的定义,从而通过己一知建立a,b,c的关系以便解出离心率。
名师圈点
如果所给几何条件能够确定动点轨迹符合椭圆、双曲线、抛物线。圆等曲线的定义,则?可直接利用,曲线定义写出方程.这种方法称为定义法(条件中常含有两对称的定点。一定点和一定直线、线段的中垂线、两圆相切等几何条件)。
考点3:圆锥曲线中的最值问题
(1)求数量积的最值;
(2)求线段长度的最值; (3)求三角形面积的最值.常常要注意字母隐含的范围(如直线与圆锥曲线相交时,△>0;图形上的点的坐标的约束范围等)
考点4:圆锥曲线中的存在性问题
(1)探究符合某条件的点的存在性;
(2)探究符合某条件的直线的存在性;
(3)探究符合某条件的图形的存在性.
名师圈点
解决存在性问题的方法为:先假设存在,由已知或假设等推出矛盾则不存在;找到了存在的对象且没有推出矛盾.则由推理论证可知存在。
考点5:圆锥曲线中的定点定值问题
(1)探究某图形过定点;
(2)探究某代数式为定值.
名师圈点
证明或探究定值问题,常常设出相关点的坐标或相关直线的方程,结合几何图形通过代数运算化简消参得定值。
