大跨度渡槽结构静力数值模拟研究

2016-09-30宋兵伟栾俊亮

东北水利水电 2016年4期

关键词：拱圈渡槽轴力

宋兵伟，栾俊亮

（大连市水利规划设计院，辽宁大连 116021）

大跨度渡槽结构静力数值模拟研究

宋兵伟，栾俊亮

（大连市水利规划设计院，辽宁大连 116021）

本文基于有限单元法以英那河渡槽为例，对大跨度拱式抛物线输水渡槽进行了系统的结构分析和数值计算，对渡槽在实际运行中所承受的各种荷载进行了分析和组合。通过静力分析计算，得出了水压力、风荷载、温度应力作用下主拱圈的内力曲线，以及其最不利内力组合。最后对英那河渡槽进行了横向和纵向稳定性的校核，其结论为拱式渡槽的静力计算和分析提供理论支持和实践经验。

大跨度；抛物线拱式渡槽；静力分析；数值模拟；英那河渡槽

0 引言

渡槽是输送渠道水流跨越河渠、道路、山冲、谷口等的架空输水建筑物，在水工建筑物中应用较广，除用于输送取水外，还可供排洪、排沙、通航和导流之用[1]。大跨度拱圈因造型美观，价格较低，养护方便，受力状态良好，在我国桥梁、水利行业被广泛采用。

英那河渡槽位于西干渠的英那河上，是西干渠的重要输水建筑物，担负着西干渠现有0.08万hm2水田的灌溉任务。原渡槽建于1973年，设计流量为8.7 m3/s，槽身采用U型槽结构型式，支撑结构采用上承式钢筋混凝土三铰肋拱，主拱圈最大跨度为80 m。经过多年的运行，渡槽槽身渗漏严重，下部排架盖梁跨中存在裂缝，致使渡槽运行存在严重安全隐患。为了保证渡槽的灌溉功能，发挥渡槽的经济效益，消除原渡槽的安全隐患，在庄河灌区2013年度续建配套与节水改造工程中对其进行拆除重建。重建后的英那河渡槽最大跨度也为80 m，拱圈结构形式统一采用无铰拱。

为了更加系统地分析大跨度无铰拱抛物线渡槽主拱圈在实际运用过程中所承受的各种荷载以及其受力特性，本文以英那河渡槽为例，根据力的传递路线，对不同荷载组合下主拱圈的内力进行了分析，而且校核了渡槽的横向和纵向稳定性。从而为其他渡槽的设计和施工提供理论支持。

1 英那河渡槽的规模与整体布置

1.1 渡槽规模

英那河渡槽主拱圈最大跨度为80 m，为大跨度结构。重建后英那河渡槽的流量为5.06 m3/s，根据文献［3］，英那河渡槽为4级建筑物，设计水深为1.35 m，满槽水深为1.8 m。

1.2 英那河渡槽纵剖面布置

英那河渡槽沿线跨越两条公路及英那河河道，全长479.80 m，纵坡比降i=0.001 63，进口底高程50.27 m，出口底高程49.49 m。槽身为钢筋混凝土U型槽，渡槽下部结构为双肋拱结构，其中24 m跨度主拱圈2座、80 m跨度主拱圈5座，主拱圈上U型渡槽为简支梁式，采取8，10，10.6 m等3种长度，自东向西分别为2跨10.6 m，3跨8 m，5×8跨 10 m，3跨8 m，1跨10.6 m。

1号和7号拱肋跨度L=24 m，1号拱肋跨高f=4.8 m，矢跨比为1/5，7号拱肋跨高f=8.0 m，矢跨比为1/3，截面宽度均为0.5 m，截面高度均为0.8 m；2—6号拱肋跨度L=80 m，跨高f=13.33 m，矢跨比为1/6，截面高度自拱顶向拱脚逐渐增加，拱顶厚1.6 m，拱脚厚1.96 m，拱肋宽0.8 m，拱脚处渐变为1.2 m，大小主拱圈拱轴线均为抛物线形，其方程为 y=4fx（L-x）/L2，其中 y为纵向坐标，x为横向坐标。

渡槽墩台采用钢筋混凝土结构，新混凝土浇筑于原毛石混凝土墩台上，新浇筑混凝土通过锚杆与原毛石混凝土进行牢固浇筑连接。

1.3 英那河渡槽横剖面布置

槽身结构计算采用熊启钧的渡槽结构计算软件相结合的方法。槽身横断面尺寸如图1所示。

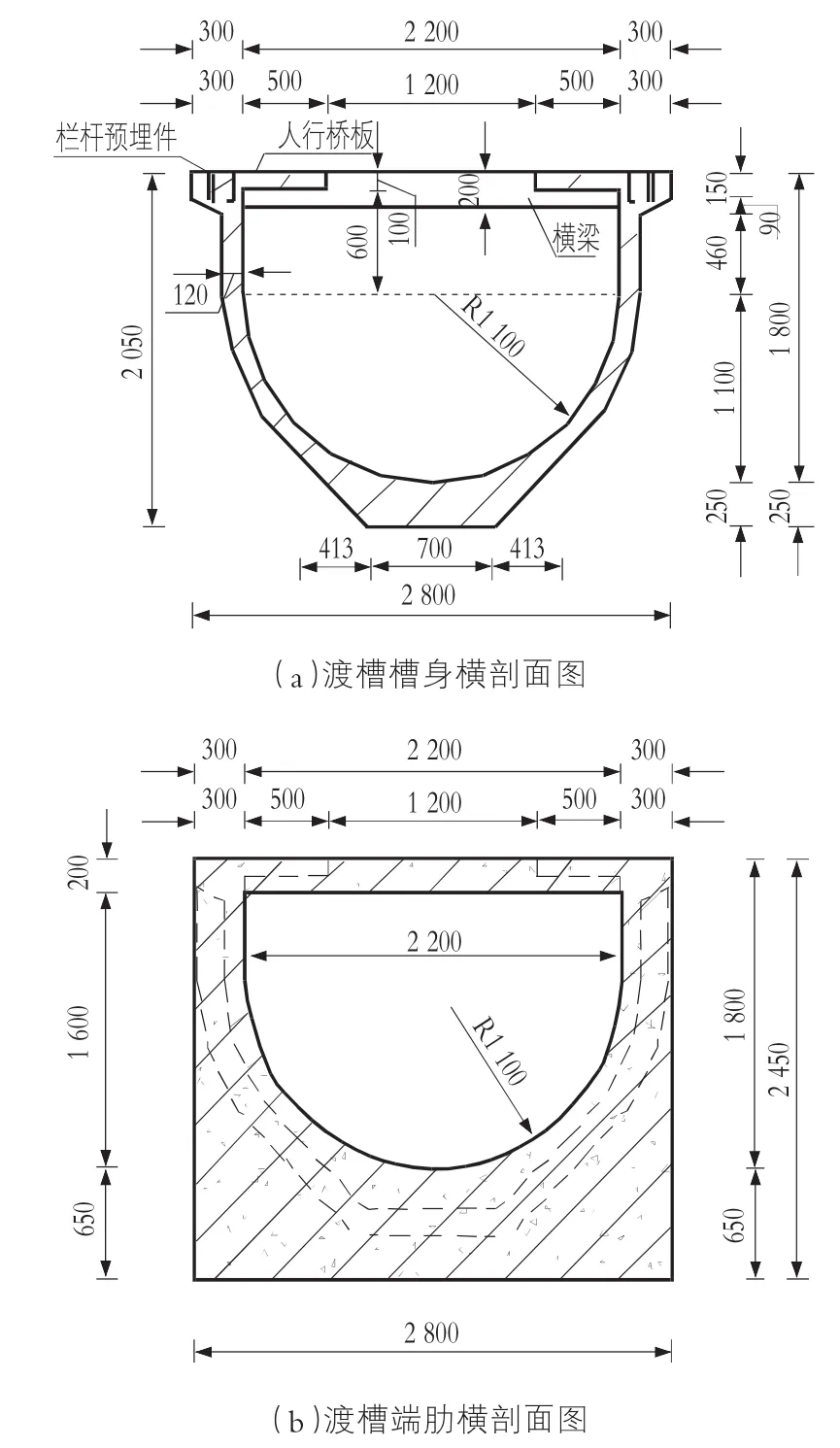
图1 渡槽槽身横剖面图

2 荷载分析

作用在渡槽上的荷载有结构重力、槽内水重、静水压力、土压力、风压力、动水压力、温度作用、混凝土收缩及徐变影响力、人群荷载、地震荷载以及施工吊装时的动力荷载等，由于该工程属地震VI度区，此次研究不考虑地震荷载。

2.1 风压力

横槽方向作用于渡槽表面的风压力，其值为风荷载强度W（kN/m2）乘以横向风力的受风面积[4]。W按下式计算：

式中：W0为基本风压值，取 0.5 kN/m2；茁z为风振系数，根据排架支撑的梁式渡槽基本自振周期T1确定；滋s为风载体形系数，空槽时取0.92，满槽时取0.96；滋z为风压高度变化系数，离地面高度为15 m时，取值为1.14；滋t为地形、地理条件系数，此次设计取1.20。

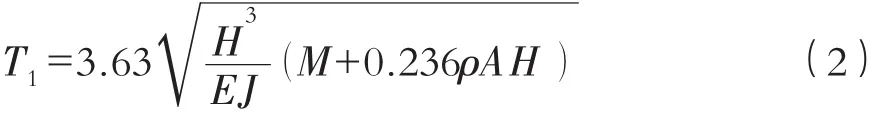
式中：H为槽身中心至地面高度，取15 m；M为搁置在排架顶部的槽身质量，空槽情况取32 503 kg、满槽情况取67 900 kg；E为排架材料的弹性模量，取 3.15×1010N/m2；J为排架横截面惯性矩，取0.376 8 m4；A为排架的横截面面积，取0.12 m2；籽为排架材料的密度，取2 500 kg/m3。

计算得：空槽时T1=0.35，满槽时T1=0.51，则茁z分别取1.32和1.40；由此得空槽时W=0.83 kN/ m2，满槽时 W=0.92 kN/m2。

2.2 温度荷载

渡槽各部构件受温度变化影响产生变形，其变形值按下式计算：

式中：△L为温度变化引起的变形值，m；L为构件的计算长度，m；△t为温度变化值，℃；琢为材料的线膨胀系数，此次研究取0.000 01。

对于中、小型渡槽，仅考虑在年温度变化（均匀的温度升高或降低）作用下引起的槽身整体变形，以及在拱圈超静定结构中引起的温度内力。温度变幅和拱的刚性越大，温度应力也越大。温度变幅根据下式确定：

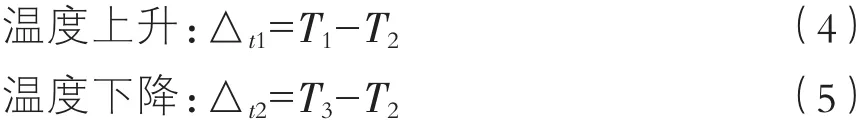
式中：T1，T3分别为最高和最低月平均气温，℃；T2为结构浇筑、安装或合拢时的气温，℃。

根据大连市2012年年鉴，渡槽所在庄河市最高月（8月）、最低月（1月）、拱圈合拢时（10月）的平均气温分别为T1=23.8℃、T2=11.6℃、T3=-10.1℃。因此△t1=12.2℃，△t2=-21.7℃。

2.3 混凝土收缩和徐变影响

此次研究渡槽主拱圈属超静定结构，因此需考虑混凝土收缩及徐变影响。

混凝土收缩而引起的附加应力，可作为相应于温度降低考虑。此次研究渡槽拱圈整体浇筑，因此按温降15℃考虑。

徐变引起的应力松弛对拱圈应力的影响是有利的[3]，计算拱圈的温度和收缩影响时，可将拱圈内力乘以影响系数，温度内力时影响系数为0.7，收缩内力时为0.45。

2.4 人群荷载

此次研究槽顶设有人行便桥，人群荷载取3 kN/m2。

2.5 荷载组合

研究渡槽静力结构计算时，所考虑的荷载工况组合：①设计工况下，自重+水重+风荷载+人群+温度（升）+混凝土收缩和徐变；②设计工况下，自重+水重+风荷载+人群+温度（降）+混凝土收缩和徐变；③空槽时，自重+风荷载+人群+温度（升）+混凝土收缩和徐变；④空槽时，自重+风荷载+人群+温度（降）+混凝土收缩和徐变；⑤满槽时，自重+水重+风荷载+人群+温度（升）+混凝土收缩和徐变；⑥满槽时，自重+水重+风荷载+人群+温度（降）+混凝土收缩和徐变。

3 计算结果分析

3.1 计算工况选择

由于工程满槽水深为1.80 m，设计水深为1.35 m，因此实际分析计算时，可只选择空槽和满槽两种工况同时考虑温度荷载的作用即可，即工况③—⑥。

3.2 计算方法

此次研究将拱轴线跨度方向上划分为80个单元，单元横向投影长度为1 m，然后根据拱轴线抛物线方程得出各个单元的横纵坐标。计算采用结构力学求解器结合midas桥梁软件进行。坐标系采用单元坐标系，x方向为拱轴线方向，y方向为水平方向，z方向与x和y方向垂直，满足右手定则。

3.3 内力分析计算

在计算工况⑤条件下拱圈内力图如图2所示。从图2中可看出，在荷载作用下，轴力表现为压力，由于自重的影响，轴力自拱顶至拱脚不断增大。剪力在排架集中力作用位置有骤减，减小值等于集中力在剪力方向上的分力。拱脚处弯矩为上部拱上部纤维受拉，集中力作用位置下部纤维受拉。拱脚处弯矩相对于其他部位弯矩较大。

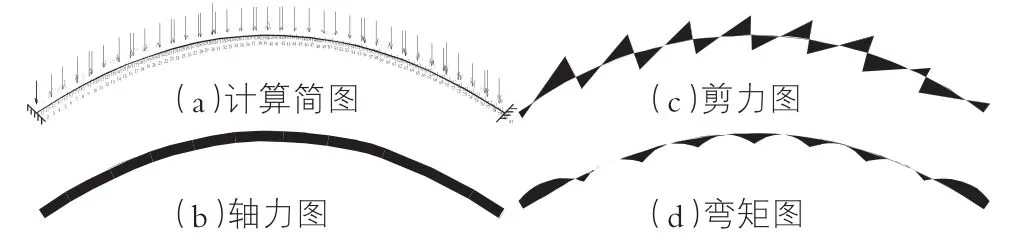
图2 渡槽拱圈计算简图内力图

该渡槽拱圈为双肋拱，由于考虑了风荷载，两拱肋所受内力不同，迎风侧拱肋轴力小，背风侧拱肋轴力大，由于拱肋单元为偏心受压构件，偏心距成为制约拱肋安全的重要因素，在两拱肋所受弯矩差异不大的前提下，轴力越小，偏心距越大。

在不同的工况下拱圈内力图如图3所示。从图3（a）可以看出，满槽时拱圈轴压力明显大于空槽时的轴力。由于渡槽拱圈为无铰拱，属超静定结构，因此无论空槽与满槽，温度升高使拱圈轴力增加，温度降低使拱圈轴力减小。由于重力的影响，使得轴压力自拱顶至拱脚大致呈抛物线形增加。排架柱集中荷载作用位置，轴力有所增加，增加的数值为排架处集中力在轴力方向上的分力。

从图3（b）中可以得出，满槽时，无论温度升高或者降低剪力值均大于空槽时的相应剪力值。温度对剪力值的影响效果不明显。

根据单元坐标系的设定，主拱圈上层纤维受拉时弯矩My为负，下层纤维受拉时My为正。从图3（c）可以看出，拱脚处的弯矩比其他部位的弯矩均较大，因此需要加强拱脚处构件的强度，在空槽（温降）工况下，拱脚处的弯矩和拱顶的弯矩大小相当；温度升高使拱圈内部的弯矩值增加；拱圈内弯矩大致呈抛物线形分布，在集中力作用位置，使拱圈下侧纤维受拉，上侧纤维受压。

由于双肋拱受横向风荷载，构件属于高次超静定空间结构，准确计算主拱圈的内力非常复杂，因此通常采用近似方法估算。此次研究首先计算出作用于槽身、拱上排架及拱圈本身承受的风压力，并以集中力和均布荷载的形式作用于横系梁节点和拱肋上，然后将拱圈按实际长度拉直，再按两端固定的平面刚架计算横向内力，其横向内力图如图4所示。图4（b）显示，风荷载作用下，迎风拱肋拱脚处的轴力为拉力，拱顶的轴力为压力而背风侧拱肋则刚好相反，因此在根据内力组合配筋计算时，要综合考虑迎风侧拱肋拱脚处、背风侧拱肋拱顶轴力减小而造成的偏心距增大问题。图4（c）显示，在风荷载作用下拱脚处迎风侧拱圈纤维受拉，背风侧拱圈纤维受压，该弯矩成为拱脚处截面横向配筋的重要依据。

图3 不同工况下渡槽拱圈内力图

图4 风荷载作用下渡槽拱圈横向内力图

3.4 横向及纵向稳定性

主拱圈横向稳定性文献［3］第5.5.8条当主拱圈宽跨比小于1/20时，应验算拱圈的横向稳定性，而且根据附录B.2的公式进行验算，此次篇幅限制，公式不再赘述，计算结果：L′=122.54，α′= 0.50，Sa=85.58，Ea=3.15 ×1010，Ia=0.07，Eb=3.15 × 1010，Tb=0.004 3，Iy′=4.42，a′=5.80，b′=2.50。

此次研究拱圈最大轴力在拱脚处为Nm=5 627.1< NL′/KH=18 291 kN，因此拱圈横向稳定性满足要求。

根据文献［3］，此次研究主拱圈矢跨比为1/6，跨高比小于30，无需进行纵向稳定性验算。