基于聚类划分的高效用模式并行挖掘算法

邢淑凝　刘方爱　赵晓晖

摘要：针对在大规模数据库中挖掘高效用模式产生大量基于内存的效用模式树，从而导致内存空间占用较大以及丢失一些高效用项集的问题，提出在Hadoop分布式计算平台下的基于聚类划分的高效用模式并行挖掘算法PUCP。首先，采用聚类的方法把数据库中相似的事务划分为若干数据子集；然后，把若干划分好的数据子集分配到Hadoop平台的各个节点中构造效用模式树；最后，把各个节点中相同项的条件模式基分配到同一个节点中进行挖掘，以减少各个节点交叉操作的次数。通过实验结果和理论分析表明：PUCP算法在不影响挖掘结果可靠性的前提下，与主流串行高效用模式挖掘——效用模式增长挖掘算法（UP-Growth）和现有的并行高效用模式挖掘算法PHUI-Growth相比，挖掘效率分别提高了61.2%和16.6%；并且使用了Hadoop计算平台，能有效缓解挖掘大规模数据的内存压力。

关键词：大数据；高效用模式挖掘；聚类；并行计算；Hadoop

中图分类号：TP301.6

文献标志码：A

0引言

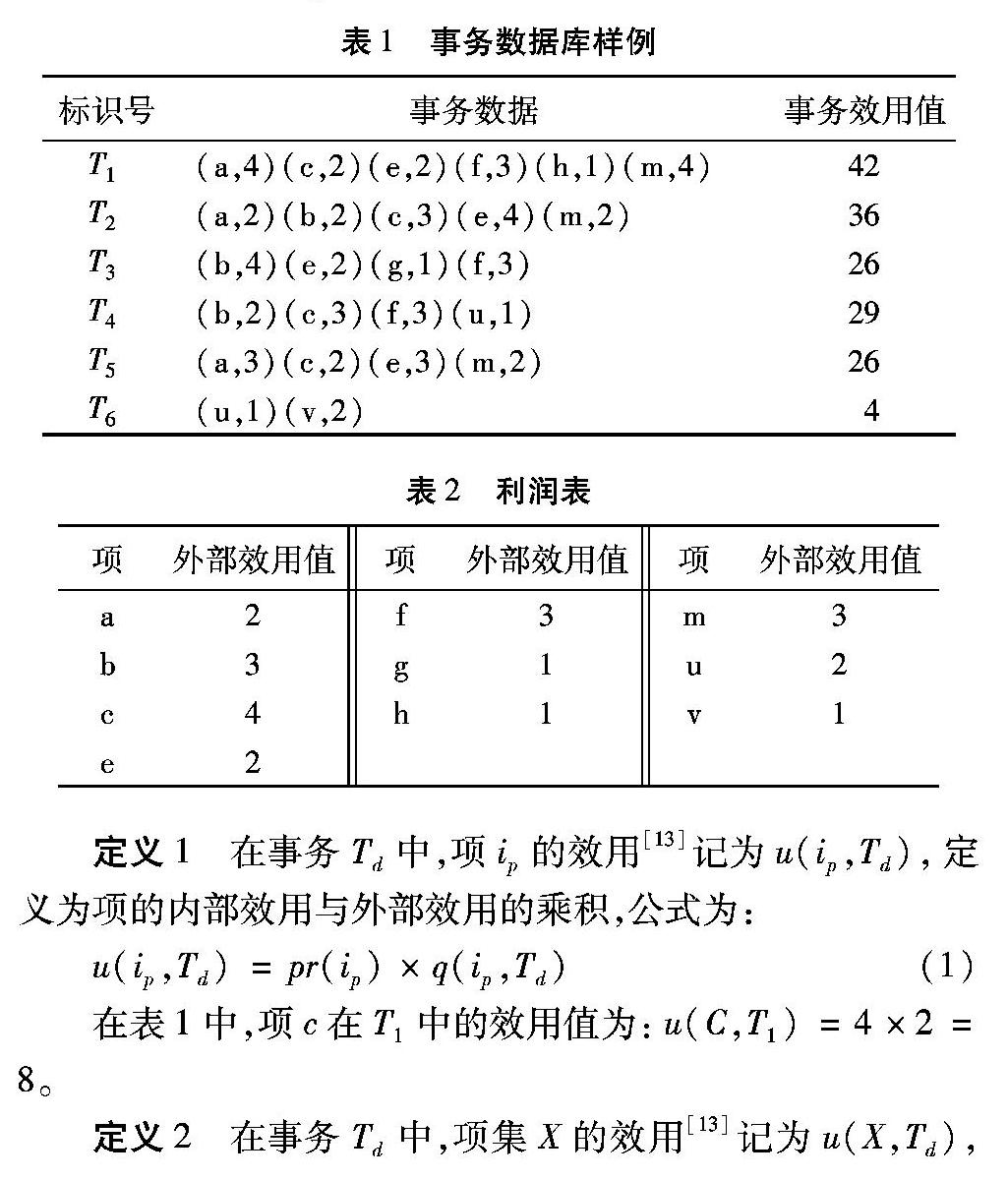
在大规模数据库中挖掘关联规则，是数据挖掘领域中一个十分重要并且具有挑战性的研究内容。频繁模式挖掘[1-2]是关联规则挖掘研究领域的一个基础课题，但其只关心项集在数据库中是否出现，而没有考虑项集在一个事务中出现的次数和项集的重要度（如利润）。因此，近几年提出了高效用模式挖掘[3-6]。在高效用模式挖掘中，每个项都有唯一的权值和在不同事务中出现的次数，如果一个项集的效用值大于或等于用户指定的最小效用阈值，则称这个项集为高效用项集。高效用项集挖掘可以应用在移动商务环境规划[7]和零售商营销[8]等多个方面。

现有的高效用模式挖掘分为两类：一类是以“产生测试”的方式进行挖掘，如Two-Phase[9]算法；另一类是以“模式增长”的方式进行挖掘，如效用模式增长（Utility Pattern Growth， UP-Growth）挖掘算法[10]。Two-Phase算法引入事务加权效用值（Transaction Weighted Utilization， TWU）这一概念，提出了高估计效用值的方法；然而，该方法需要多次扫描原始数据库并且会产生大量的候选高效用项集。为了解决这一问题，算法UP-Growth引入效用模式树（Utility Pattern Tree， UP-Tree）结构，以“模式增长”的方式进行挖掘，并提出DGU（Discarding Global Unpromising items）、DGN（Discarding Global Node utilities）、DLU（Discarding Local Unpromising items）和DLN（Decreasing Local Node utilities）四个策略来减少候选高效用项集的数量。算法UP-Growth+[11]为了减少局部的效用值，在UP-Growth算法的基础上进行了改进，将DLU和DLN策略改进成DNU（Discarding local unpromising items and their estimated Node Utilities）和DNN（Decreasing local Node utilities for local UP-Tree by estimated utilities of descendant Nodes）策略。

目前现有的高效用模式并行挖掘算法较少，文献[12]探讨应用MapReduce编程模型实现并行的挖掘，提出了算法PHUI-Growth（Parallel mining High Utility Itemsets by pattern-Growth），但是该算法并没有深入研究数据集的分块处理和降低数据通信开销的方法，并且使用“产生检测”的方式进行挖掘，在挖掘过程中可能存在丢失高效用项集、产生大量的候选项集等问题，而且还需要利用大量的内存空间来存储非候选项集，增大了内存开销。针对这些问题，本文提出了一种基于聚类划分并且使用Hadoop分布式计算平台挖掘高效用模式的算法——PUCP（Parallel Utility mining based on Cluster Partition）。该算法采用“模式增长”的方式进行挖掘，以聚类划分的方式对原始数据库进行水平划分，通过将互不重叠的数据子集分配给不同的Hadoop中的节点进行处理，以增大并行粒度，减小交叉操作的规模，确保获得完整的高效用模式，提高并行挖掘效率。

具体步骤如下：

步骤1

在Hadoop平台master主节点中，按照UP-Growth算法的第一步对整个数据库中的数据进行处理，即去掉TWU小于minutil的项，并且将事务中的项按照TWU降序的顺序进行重新排序。利用Jaccard相似度系数对处理过的数据库中事务进行水平聚类划分，将相似的事务划分到一起，作为一个数据子集，将这些数据子集由主节点master分配到Hadoop平台中的不同slave从节点中进行处理。如图1中的第一阶段所示。

步骤2

每个salve节点根据本文提出的新的建树算法产生效用模式树，该算法是在UP-Growth算法的基础上进行的改进，在树节点中设置一个前缀效用和（pru）域，由文献[3]描述的前缀效用和可知，前缀效用和更加接近项集真实的效用值，以此来减少候选高效用项集的数量。如图1中的第二阶段所示。

步骤3

每个slave节点根据效用模式树，依据本文提出的改进的条件模式基结构产生该树所有项的条件模式基。

步骤4

把每个salve节点中相同项的条件模式基分配到同一个节点中进行处理，也就是说，一个节点中只存储一个项（如：im）的全部条件模式基，并将项im所有条件模式基中的MIU域进行比较，得到一个最小值作为项im的全局MIU值。如图1中的第三阶段所示。

步骤5

每个节点根据项的条件模式基产生条件效用模式树，采用UP-Growth算法中的DLU和DLN策略递归产生候选高效用项集。

步骤6

将所有节点产生的候选高效用项集汇聚到master节点中，扫描划分后的数据库，计算所有候选高效用项集的真实效用值，得到高效用项集。如图1中的第四阶段所示。

2.1局部节点的具体处理过程如下：

步骤1

对重排序后数据库中的事务进行水平聚类划分。

针对分类属性数据（特别是购物篮数据）的特性，本文采用Jaccard相似度系数sim（T1，T2）对重排序后数据库中的所有事务进行水平聚类划分。把每个数据子集当中的第一个事务作为代表点，新的事务与每个数据子集中的代表点比较相似度，将其划入最相似的数据子集中，即如果相似度小于用户指定的阈值，则将其划入新的数据子集中。当产生的数据子集的个数达到k-1后，就将第k个数据子集作为与前k-1个数据子集不相似的事务的集合。该算法的时间主要耗费在与每个数据子集的代表点进行比较上，因此，整个算法的时间花费是小于kn的，该算法具有较高的时间效率。以表1数据库为例，对重新排列后的事务进行水平聚类，根据sim函数计算后得到3个数据子集，如图2所示：数据子集D1包含事务T1、T2、T5；数据子集D2包含事务T3、T4；数据子集D3包含事务T6，由于T6中的项都是非高效用项，所以经过计算删除后得到的是一个空集。

步骤2

对聚类划分后的数据子集建立效用模式树。

在每个slave节点中按照本文建树的伪代码来构造效用模式树。其中，树中的每个节点有四个域：name域用来标识项，pru域用来记录节点的前缀效用和，count域记录节点出现的次数，parent域记录每个节点的父节点。以图2中的数据为例，由于数据子集D3中没有候选高效用项，因此不能产生效用模式树，数据子集D1、D2的效用模式树分别如图3（a）、（b）所示。

每个slave节点构造完效用模式树，根据该效用模式树产生项条件模式基，该条件模式基有三个域：路径效用域记录路径的效用值，支持度域记录路径出现的次数，MIU域记录项在计算节点的最小效用值。根据图3的效用模式树，表3、4分别是D1和D2的局部条件模式基。

步骤3

一个节点只处理一个项的全局条件模式基。

将步骤2中每个salve节点中的一个项（如项im）的局部效用模式基合并到一个节点中进行处理，该节点得到im的全局效用模式基，同时得到im的局部MIU值，经过比较这些MIU值可以得到im的全局最小效用值。在该节点中利用UP-Growth算法中的步骤DLU和DLN策略对全局条件模式基进行挖掘，得到候选高效用项集。

步骤4

将所有节点中的候选高效用项集合并到master主节点中计算它们的真实效用值，以此得到全局高效用项集。

3实验与结果分析

3.1实验环境及数据集

将本文提出的PUCP算法与主流的串行挖掘算法UP-Growth和现有并行算法PHUI-Growth进行对比实验。

实验平台：实验环境采用基于云计算平台Hadoop的计算集群，共有6个节点（1个主控节点（master），5个数据节点（slaves））；JDK是openjdk-6-jdk，Hadoop的版本采用0.21.0版。

实验数据集：本实验的数据集都由真实数据集组成，真实数据集的特征如表5所示。其中：|D|代表的是一个数据集中事务的数目，Tavg是事务的平均长度，|I|是数据集中项的数目。这些数据可从FIMI（Frequent Itemset Mining Implementations repository）[15]网站中下载。Chain-store和Retail这两个数据集中都已经包括了数据的内部效用值和外部效用值。Mushroom数据集自身不包括内部效用值和外部效用值，本实验给每个项随机地产生一个大于0小于10的整数作为内部效用值；项的外部效用值也是随机产生的一个大于等于0.01小于等于10的数值，并且该数值符合对数正态分布。

3.2实验结果的分析

3.2.1查全结果实验

由于PHUI-Growth算法并没有深入研究数据集的分块处理，因此挖掘出的高效用项集会丢失一些项集，并且随着事务长度的增大，丢失的项集会增多。本实验在数据集Mushroom中进行，设定事物长度为50～70，每次事物长度增加5，分别比较PUCP算法、UP-Growth算法和PHUI-Growth算法产生高效用项集的数量，结果如表6所示。可以看出，随着事务长度的增加，UP-Growth算法和PUCP算法所查找出的项集数量均比PHUI算法多，并且UP-Growth算法和PUCP算法所查找出的项集数量相差不大。

3.2.2挖掘结果的准确性实验

在数据集Mushroom进行实验，以对比三种算法的正确率，结果如图4所示。从图4可以看出：随着效用阈值的不断减小，三个算法挖掘结果的正确率随之降低；三个算法在同一效用阈值下，正确率基本一致，并且维持在75%左右，这说明本文提出的PUCP算法在提高效率的同时不会影响挖掘结果的准确性。

3.2.3算法的运行时间实验

在高效用模式挖掘算法中，算法运行时间会随着最小效用阈值的降低而增加，本实验主要测试在不同最小效用阈值时算法运行时间的对比。

在数据集Mushroom中，实验假定项集长度为14，在相同的最小效用阈值下，三个算法在该数据集中运行5次，取5次运行时间的平均值，结果如图5所示。从图5可以看出，在越稠密的数据集中，最小效用阈值越小，挖掘过程中产生的候选高效用项集的个数会越多，从而导致算法的运行时间增长。PUCP算法和PHUI-Growth算法的运行时间明显少于UP-Growth算法，这是由于前两个算法使用6台机器组成的Hadoop集群并行地进行挖掘；并且随着阈值的减小，UP-Growth算法的运行时间增加得越明显。由于采用聚类划分的方法将相似的事务放到一个计算节点中，因此每个节点中树结构较小，遍历树的时间较短，PUCP算法整体的运行时间要小于PHUI-Growth算法。

3.2.4算法内存消耗实验

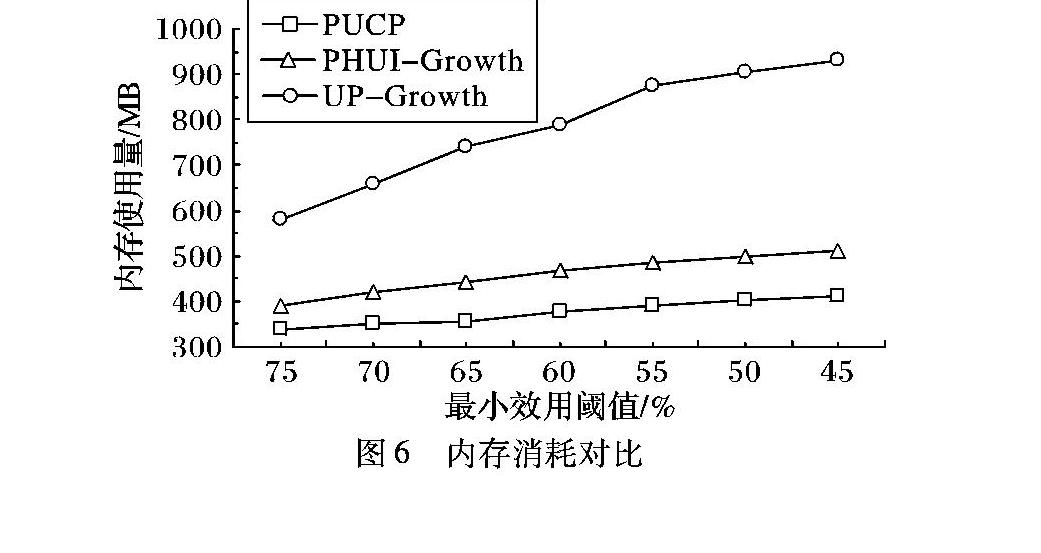
本实验主要测试在不同最小效用阈值时三个算法在Chain-store数据集中的内存消耗对比。实验内存消耗的提取方法如下：在算法运行的过程中，插入多个测试点，在每个测试点中，先强行删除算法运行过程中产生的垃圾节点，再提取出当时的内存消耗值，并以这些值中的最大值作为当前算法的内存消耗值。运行结果如图6所示。

由图6可以看出，随着最小效用阈值的降低，UP-Growth算法内存消耗越来越大，这是因为随着最小效用阈值的降低，效用模式树中的节点增多；但PUCP算法和PHUI-Growth算法的内存消耗基本没有太大变化，这是因为这两个算法采用并行的策略；PUCP算法采用聚类划分方法将相似的事务建成效用模式树，树结构的分支少，并且采用模式增长的方式进行挖掘，减少了候选项集的数量，采用树形结构，不存储非候选项集，因此所占内存比PHUI-Growth算法要少。

4结语

本文在Hadoop计算平台下，提出了基于聚类划分的高效用模式并行挖掘算法PUCP，该算法通过计算相似度Jaccard系数，将大规模数据库聚类划分成若干数据子集，并将这些数据子集分配到Hadoop若干计算节点中实现并行挖掘。本文采用3个典型的真实数据集进行验证，结果表明算法PUCP在时间和空间方面效率都有所提高。目前高效用模式挖掘理论研究逐渐成熟，在今后的研究工作中，将着重考虑在挖掘的过程中高效地利用Hadoop平台系统的计算、存储资源以及容错、优化负载均衡等问题。

参考文献：

[1]JAGRAW R， SRIKANT R. Fast algorithms for mining association rules [C]// Proceedings of the 20th International Conference on Very Large Data Bases. San Francisco， CA： Morgan Kaufmann， 1994： 487-499.

http：//cs.stanford.edu/people/chrismre/cs345/rl/ar-mining.pdf

[2]HAN J W， KAMBER M.数据挖掘：概念与技术[M].范明，孟小峰，译.2版.北京：机械工业出版社，2007：206-228. （HAN J W， KAMBER M. Data Mining： Concepts and Techniques [M]. FAN M， MENG X F， translated. 2nd ed. Beijing： China Machine Press， 2007： 206-228.）

[3]ZIHAYAT M， AN A. Mining top-k high utility patterns over data streams [J]. Information Sciences， 2014， 285： 138-161.

[4]YUN U， RYANG H. Incremental high utility pattern mining with static and dynamic databases [J]. Applied Intelligence， 2015， 42（2）： 323-352.

[5]YUN U， RYANG H， RYU K H. High utility itemset mining with techniques for reducing overestimated utilities and pruning candidates [J]. Expert Systems with Applications， 2014， 41（8）： 3861-3878.

[6]SONG W， LIU Y， LI J. Mining high utility itemsets by dynamically pruning the tree structure [J]. Applied Intelligence， 2014， 40（1）： 29-43.

[7]SHIE B-E， HSIAO H-F， TSENG V S. Efficient algorithms for discovering high utility user behavior patterns in mobile commerce environments [J]. Knowledge and Information Systems， 2013， 37（2）： 363-387.

[8]LEE D， PARK S-H， MOON S. Utility-based association rule mining： a marketing solution for cross-selling [J]. Expert Systems with Applications， 2013， 40（7）： 2715-2725.

[9]LIU Y， LIAO W-K， CHOUDHARY A. A two-phase algorithm for fast discovery of high utility itemsets [M]// PAKDD 05： Proceedings of the 9th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining. Berlin： Springer-Verlag， 2005： 689-695.

[10]TSENG V S， WU C-W， SHIE B-E， et al. UP-Growth： an efficient algorithm for high utility itemset mining [C]// KDD 10： Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2010： 253-262.

[11]SHIE B-E， HSIAO H-F， TSENG V S. Efficient algorithms for discovering high utility user behavior patterns in mobile commerce environments [J]. Knowledge and Information Systems， 2013， 37（2）： 363-387.

[12]LIN Y C， WU C-W， TSENG V S. Mining high utility itemsets in big data [C]// PAKDD 2015： Proceedings of the 19th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining， LNCS 9078. Berlin： Springer-Verlag， 2015： 649-661.

[13]LIU Y， LIAO W-K， CHOUDHARY A. A fast high utility itemsets mining algorithm [C]// UBDM 05： Proceedings of the 1st International Workshop on Utility-based Data Mining. New York： ACM， 2005： 90-99.

[14]JAIN A K， DUBES R C. Algorithms for clustering data [M]// Algorithms for Clustering Data. Upper Saddle River， NJ： Prentice Hall， 1988： 227-229.

[15]Frequent itemset mining implementations repository [EB/OL]. [2015-12-22]. http：//fimi.cs. Helsinki.fi.