基于优化的熵权灰色关联法对建筑业的发展评价

李　米　郑晓云

(东北林业大学土木工程学院，黑龙江 哈尔滨　150040)



基于优化的熵权灰色关联法对建筑业的发展评价

李米郑晓云

(东北林业大学土木工程学院，黑龙江 哈尔滨150040)

以黑龙江省为例，选取建筑企业个数、劳动生产率、技术装备率等九个评价指标，结合相关统计数据，利用优化的熵权灰色关联分析法计算了灰色关联系数，确定了黑龙江省内2014年各城市建筑业综合发展水平的排序结果，并应用该方法实证研究了黑龙江省建筑业的综合发展情况，指出该方法具有较强的可操作性。

建筑业，熵值法，灰色关联分析，指标权重

随着我国经济的快速发展，人们物质文化生活水平的提高，建筑业作为衡量我国现代化水平的重要标志，在国民经济总产值中占有很大的比重。因此如何引导建筑业的蓬勃发展便得到了全国各地区部门的高度重视。近年来我国学者对影响建筑业可持续发展的因素分析取得了丰硕的成果。例如姜连馥利用模糊聚类和粗糙集理论研究了综合评价建筑业的方法和步骤，评价了中国的八大省建筑业的综合实力[1]；王苏岩，崔旖娜将产业经济学相关理论与投入产出分析相结合，研究了建筑业在国民经济中的重要地位，对辽宁省建筑业发展现状进行了客观的评价[2]；张长根、李涛从建筑业综合实力的角度，利用因子分析法对各地区建筑业的综合实力排名[3]。以上研究均取得了丰富的成果，对我国建筑业未来的发展起到了积极重要的作用。

熵权灰色关联分析法是将熵值法[4]与灰色关联分析法[5]相结合的分析评价方法。它以那些已知信息不全面，统计数据不充分的评价体系为研究对象，利用熵值法计算权重更客观的优势，结合灰色关联法更适用于少量样本系统的优点，对数据进行加工和处理，利用对比分析，从而得出结论的一种分析评价方法。在传统的熵权灰色关联分析中，分辨系数ζ没有量化(通常ζ=0.5)，且对指标权重的计算方法存在不足。本文在传统熵权灰色关联分析法的基础上进行两方面改进：第一量化分辨系数ζ的取值，第二改进权重计算式。最后应用优化的熵权灰色关联分析法对黑龙江省2014年各市区建筑业的综合发展进行实证研究[8]，分析2014年黑龙江省建筑业整体发展趋势，为引导建筑业可持续发展提供参考方向。

1　熵权灰色关联分析计算过程

1.1传统熵权灰色关联分析法

1)灰色关联度的计算。

a.原始数据的无量纲化，假设X0为参考序列，Xi为比较序列。

正向指标：

X0j=max(X1j,X2j,…,Xmj)

(1)

负向指标：

X0j=min(X1j,X2j,…,Xmj)

(2)

(3)

b.计算绝对差及关联系数。

绝对差：

(4)

关联系数：

(5)

其中，分辨系数ζ=0.5；两级最小差Δ(min)=min minΔij;两级最大差Δ(max)=max maxΔij。

c.计算灰色关联度。

(6)

2)指标权重的计算。

a.标准化原始数据。

正向指标：

(7)

负向指标：

(8)

(9)

b.计算信息熵及信息效用值。

(10)

信息效用值：

dj=1-ej(j=1,2,…,n)

(11)

c.计算各指标权重。

(12)

1.2优化的熵权灰色关联分析法

由上文可知，分辨系数ζ的取值会直接影响关联系数γ的计算结果，因此ζ的合理取值是该方法成功运用的关键。现引入一变量εΔ来量化分辨系数ζ的取值[6]。通过指标权重的计算式可以看出,当信息效用值dj愈加趋近于1时，各指标间微小的差别就可引起计算结果的改变，因此对指标权重计算式加以改进[7]。优化的熵权灰色关联分析法不仅改正了ζ取值不当使评价结果失真的可能，还避免了指标权重计算过程中的主观性，使评价结果更符合实际。具体方法如下。

1.2.1量化分辨系数ζ

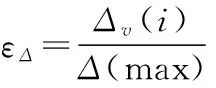
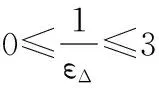
优化后关联系数求法如下：

(13)

1.2.2优化权重计算式

通过分析，权重计算式改进如下：

(14)

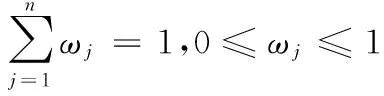
2　实例分析

2.1评价指标的选取

本文以黑龙江省2014年建筑业相关统计数据为例，坚持科学性和可操作性的原则，对黑龙江省内各市区的建筑业可持续发展进行实证研究。征求相关专家意见，在有效性、科学性的基础上选取建筑企业个数X1(个)、从业人员数量X2(人)、自有机械设备数量X3(台)、劳动生产率X4(元/人)、技术装备率X5(元/人)、动力装备率X6(kW/人)、房屋建筑面积竣工率X7(%)、人均利税X8(元/人)及资产负债率X9(%)九个指标作为影响建筑业可持续发展的评价指标。各指标统计数据均来自《黑龙江省统计年鉴2015》(见表1)。

表1　2014年黑龙江省建筑业发展相关指标原始数据

2.2灰色关联度的计算

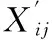
根据式(4)计算绝对差，根据1.2.1中的方法确定ζ的取值，计算结果见表2。根据式(13)计算灰色关联系数，见表3。

表2　分辨系数

2.3指标权重的计算

根据式(7)～式(9)计算得到标准化后的矩阵Y，根据式(10)，式(11)计算信息熵及效用值，最后依据式(14)计算得到各指标权重，见表4。

2.4计算灰色关联度

根据式(6)确定评价对象的灰色关联度及排序，计算结果见表5。

3　评价结果及分析

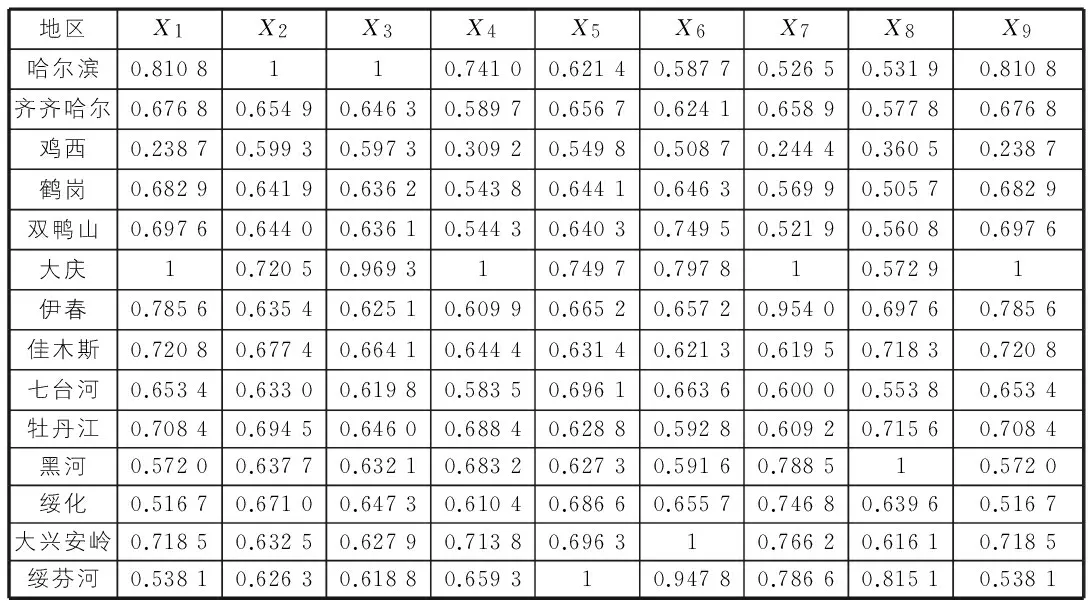
表3　灰色关联系数

表4　评价指标的权重

。

1)黑龙江省2014年建筑业综合发展水平地区差异较明显。大庆、哈尔滨、绥芬河、大兴安岭、伊春建筑产业资源配置相对较好，可持续发展水平较高。双鸭山、绥化、七台河、鹤岗和鸡西相对较弱。黑河、佳木斯、牡丹江、齐齐哈尔介于二者之间。

2)通过优化的熵权灰色关联分析法可以看出，建筑业市场的资源配置大多集中在大庆、哈尔滨等较发达的城市，鸡西、鹤岗等城市建筑业的资源配置相对较匮乏。针对这一差异，政府应制定有倾向性的相关政策强化落后地区的资源配置，提高技术效率和企业竞争力，提升技术装备率、动力装备率以及劳动生产率等指标，增加自有机械设备数量，加大资金及人才的投入，缩小地区差异，使黑龙江省整体的建筑业市场发展更均衡。

4　结语

要实现建筑业的蓬勃发展，选择客观、合理的评价方法至关重要。本文在传统熵权灰色关联分析法的基础上，量化了关联系数，优化了权重的计算，使评价结果更严谨。基于优化的熵权灰色关联分析法综合分析黑龙江省2014年建筑业的整体发展水平，为政府和相关部门进行科学决策提供依据，对今后黑龙江省建筑业调整产业结构，提高发展质量，实现建筑强省的目标提供了一定的参考方向。

[1]姜连馥,石永威,满杰,等.基于模糊粗糙集理论的建筑业综合评价[J].大连理工大学学报,2007,47(5):729-734.

[2]王苏岩,崔旖娜.基于产业经济学理论的建筑业评价[J].建筑经济,2007(S2):27-29.

[3]张长根,李涛.因子分析法对建筑业综合实力的评价[J].建筑经济,2003(12):47-49.

[4]齐宝库,李长福.基于熵值法的建筑业可持续发展评价实证研究——以辽宁省为例[J].科技管理研究,2014,34(5):69-73.

[5]邓聚龙.灰理论基础[M].武汉：华中科技大学出版社,2002.

[6]东亚斌,段志善.灰色关联度分辨系数的一种新的确定方法[J].西安建筑科技大学学报(自然科学版),2008,40(4):589-592.

[7]侯保灯,李佳蕾,潘妮,等.基于改进熵权的灰色关联模型在湿地水质综合评价中的应用[J].安全与环境学报,2008,8(6):80-83.

[8]王秀兰.熵权灰色关联法在区域卫生资源配置中的应用[J].产业与科技论坛,2016,15(7):55-58.

[9]江文奇.无量纲化方法对属性权重影响的敏感性和方案保序性[J].系统工程与电子技术,2012,34(12):2520-2523.

[10]郭亚军,易平涛.线性无量纲化方法的性质分析[J].统计研究,2008,25(2):93-100.

Study on construction industry based on ameliorated entropy weight grey correlation method

Li MiZheng Xiaoyun

(School of Civil Engineering, Northeast Forestry University, Harbin 150040, China)

In Heilongjiang Province as an example, select nine evaluation indexes: construction enterprise number, labor productivity, technology and equipment rate, combined with the relevant statistical data, using the optimized entropy weight and gray correlation analysis method to calculate the grey relational coefficient determined the ranking results of the urban construction industry comprehensive development level of Heilongjiang Province in 2014. By using this method, the comprehensive development of construction industry in Heilongjiang Province is studied. It is proved that the method is workable.

construction industry, entropy method, grey correlation analysis, index weight

1009-6825(2016)25-0230-03

2016-06-24

李米(1989- )，女，在读硕士；郑晓云(1972- )，女，硕士生导师，副教授

F120.4

A