环境温度对桥梁结构动态特性影响的研究进展★
2016-09-29付光来刘天齐
夏 呈 付光来 刘天齐
(1.东南大学土木工程学院,江苏 南京 210018;2.国家电网山东省电力公司经济技术研究院,山东 济南 250021;3.江苏省靖江市高级中学,江苏 靖江 214500)
·桥梁·隧道·
环境温度对桥梁结构动态特性影响的研究进展★
夏呈1付光来2刘天齐3
(1.东南大学土木工程学院,江苏 南京210018;2.国家电网山东省电力公司经济技术研究院,山东 济南250021;3.江苏省靖江市高级中学,江苏 靖江214500)
从温度引起材料性质变化、超静定结构产生温度应力、结构温度分布多样等方面,分析了温度对结构影响的作用机理,并论述了温度—模态频率的研究进展,对温度—模态频率模型的研究方向进行了展望。
环境温度,桥梁结构,模态频率,动态特性
0 引言
随着交通的发展以及人们对建筑工程结构的更深层次的认识,基础建设的周期不仅仅局限在设计施工,对重大工程结构的维护以及损伤预警变得尤为重要,这关乎到人民的生命财产安全。结构工作者已经开始把结构健康监测作为一个重要的研究领域,随着研究的发展,相信结构健康监测不仅仅主要应用于重要工程结构,健康监测发展完善后必定会在减少工程事故,保护生命财产上发挥重大作用。
大量研究实践、试验表明,结构损伤会引起结构动态特性的改变,我们可以通过监测桥梁结构的动态特性变化来反推结构损伤情况,结构健康监测自提出以来,总体思路已经确定,它的理想是通过监测工程结构动态特性的变化来分析结构的整体健康状况以及结构的损伤,以便于能够及时的采取措施保证生命安全或及时维修结构延长工程结构的使用寿命。然而受环境限制,结构的动态特性还会受到各种环境因素的影响。环境因素往往是多种多样的,包括温度、风、车辆荷载等,其中温度对桥梁结构动态特性的影响受到了国内外学者的关注。
研究表明:温度变化引起的模态频率波动可以淹没许多结构损伤所引起的变化,甚至可以造成对结构动力特性的误解。张通[1]提到:桥梁结构1阶模态频率的变化幅度可达5%。Peeters和Roeck等对瑞士Z24桥进行了长期测试,发现该桥1阶~4阶 模态频率的波动范围分别达到14%,18%,17%和16%。李爱群等通过对润扬大桥斜拉桥监测研究发现,环境激励下该桥整体振动的模态频率在1 d内可以发生约1%~4%的变化。可见温度的影响非常明显,对桥梁结构损伤的影响产生了很大的干扰。因此量化温度因素对结构动态特性的影响,总结更精确的消除温度影响的方法,能够对健康监测的更好应用提供支持,意义重大。
1 温度影响的作用机理
温度对结构的影响是多方面的,复杂的,温度对结构动态特性的影响主要从温度引起材料性质变化,超静定结构产生温度应力,大型结构温度分布多样等方面考虑。
1.1温度引起材料性质变化
研究表明温度对材料性质的影响主要是引起弹性模量、热膨胀系数等的改变。
利用有限元软件ANSYS,改变材料的弹性模量进行频率分析。

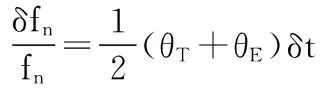
式中:θT——材料的热膨胀系数;
θE——弹性模量随温度的变化率。
上述研究是假设结构的截面上为同一温度,并没有考虑温度在截面上的传递,根据热量传递的基本规律,当物体内部各部分之间存在温差时,就会有热量从温度较高的部分传递到较低的部分,形成导热现象。对各向同性材料,内部导热与温度之间的关系遵从导热基本定律。因此,考虑温度沿截面高度分布影响的频率相对变化量与温差的关系还有待研究。
1.2超静定结构产生温度应力
混凝土桥梁结构的温度应力可以分成两个部分:
1)温度变形受到内部各部分的相互约束而引起的应力,称为自约束温度应力或温度自应力;
2)超静定结构中温度变形受到外部约束而引起的应力,称为温度次应力。静定结构中只有温度自应力,超静定结构的温度应力由上述两部分应力叠加而成。
如下是利用有限元软件分析某桥梁结构在不同温度下的应力。图1为分析模型,图2为桥梁模型简图。
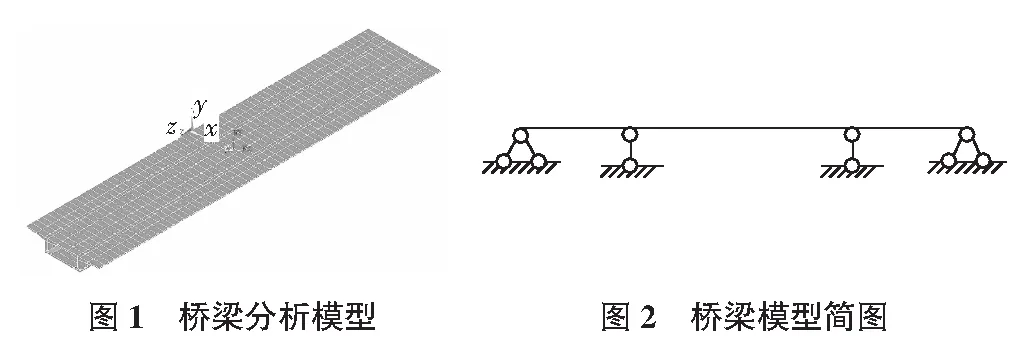
对箱梁做温度变化分析,假设温度从外表面到内表面沿厚度方向线性递减。
t=t0×(h-hx)/h。
式中:t0——外表面温度;
h——箱梁底板(或顶板、腹板)的厚度;
hx——厚度方向坐标。
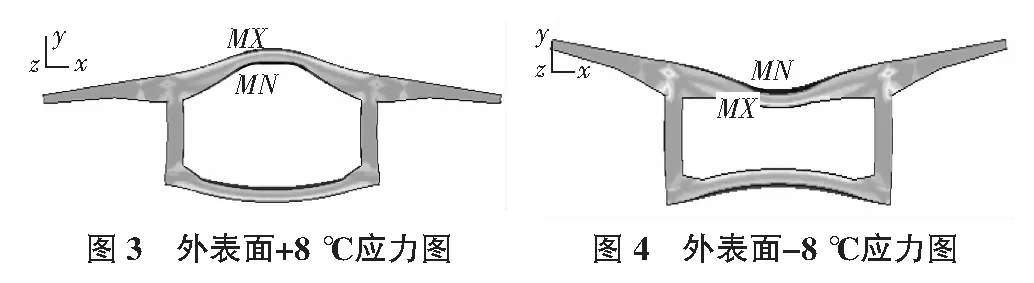
当设置t0分别为+8 ℃,-8 ℃时,应力见图3,图4。
对比图3,图4可以看出,当温度为+8 ℃,-8 ℃时,箱梁应力或变形均有很大差异,温度在桥梁结构内部产生的温度应力是很显著的。
温度对超静定结构产生的应力相当于给结构施加了一系列荷载,相比较自然状态下结构的振动会受到影响,必然会改变结构的振动特性。
1.3桥梁等大型结构温度分布多样
桥梁结构体型巨大,长度—宽度—高度三个方向的温度分布各异,同一方向温度分布也有很大差距。对于箱梁截面沿其高度的温差分布,国内外学者做了大量实验研究。叶见曙等[3]通过对混凝土箱梁温度实测数据的回归分析,证明在日照作用下,箱梁截面沿其高度的温差分布确为非线性分布,温差计算模式建议为箱梁顶板上边缘最大温度差值为20 ℃,向下至腹板按指数函数Ty=20e-5y分布;而底板下边缘最大温差为1.5 ℃,并在距离底面200 mm高度内按线性变化;沿桥纵向不同位置、不同高度的箱梁截面混凝土温度观测与分析表明,在日照作用下,它们具有一致的温度分布形式和计算模式。可见温度分布应当是对温度—模态频率模型影响明显。
对于温度场的研究国内外学者做了大量工作。我国公路桥规[4]规定了竖向温度梯度曲线——与梁高相关的一条折线。欧洲规范、美国规范也有自己的温度梯度模式。
目前,桥梁设计真正考虑了温度梯度的影响,然而在健康监测中由于温度分布多样,算法复杂,一般忽略温度梯度的影响,把温度作为一个均匀分布的量来考虑,很少真正把温度分布及梯度传递量化到温度—结构模态频率的算法中去。
2 温度—模态频率模型的研究进展
针对由环境激励响应辨识得到的桥梁模态频率会受到温度影响的问题,通过建立模态频率—温度分布模型是识别温度对桥梁结构模态频率影响的重点,国内外许多学者在建立模型方面提出了许多方法和见解,主要有利用多项式建立温度—模态频率回归模型、利用神经网络建立温度—模态频率回归模型,以及利用支持向量机建立温度—模态频率回归模型。
1)利用多项式建立温度—模态频率回归模型。
多项式建立回归模型思想相对简单一些,多项式模型为:
f(x)=P1xn+P2xn-1+…+Pn-2x3+Pn-1x2+Pnx+Pn+1。
式中:x——变量值;
f(x)——函数值;
Pi(i=1~n)——回归模型的系数。
邓扬[9]应用6次多项式模型建立润扬长江大桥悬索桥模态频率f与温度T的季节相关性回归公式,很好的描述了润扬长江大桥模态频率和温度的季节相关性。
2)利用神经网络建立温度—模态频率回归模型。
人工神经网络最初是为模拟人的大脑功能而提出来的,是由大量的、功能比较简单的神经元互相连接而构成的复杂网络系统。通过对网络进行训练,网络可以获得相关信息,并将信息存储在神经元的连接权值中。利用神经网络进行损伤识别,多采用多层BP网络。BP网络结构简单,学习、训练算法较为成熟,对多层BP网络,采用适当的权值和激活函数,可以对任意非线性映射进行任意程度的近似。
丁幼亮等[6]采用神经网络技术建立桥梁实测模态频率与温度的相关性模型,用以消除温度变化对模态频率的影响。然后,将不同温度下的实测模态频率进行“温度归一化”,在此基础上利用神经网络新奇检测技术建立自联想神经网络进一步识别模态频率的异常变化。通过润扬大桥悬索桥236 d的实测数据分析验证了该方法的可行性。分析结果表明,不同季节下模态频率的相对变化平均约为2.0%,采用所提方法可以识别出悬索桥模态频率0.1%的异常变化,适用于悬索桥结构的在线整体状态监测。
3)利用支持向量机建立温度—模态频率回归模型。
支持向量机(Support Vector Machines,SVM)与神经网络类似,都是学习型的机制,但与神经网络不同的是SVM使用的是数学方法和优化技术。SVM的一般做法是:将所有待分类的点映射到“高维空间”,然后在高维空间中找到一个能将这些点分开的“超平面”。
支持向量机是一种非常有用的统计学理论,在建立桥梁结构的温度—模态频率回归模型中经常用到。樊可清等[8]对汀九大桥长期振动和温度分布测试数据进行了分析研究,采用支持向量机技术建立桥梁实测模态频率与温度的相关性模型,并给出了运用SVM的非线性回归算法消除温度影响的具体方法以及运用这种方法对汀九大桥600 h连续测试数据的处理结果。结果证明支持向量机(SVM)的非线性回归模型可以有效地消除引起模态频率变化的环境温度和温度分布模式因素的影响。
3 结论与展望
温度变化作为环境因素的一个主要方面,对结构模态频率的影响很大,往往会淹没结构真正的损伤,然而温度的影响复杂多变,不仅体现在温度变化上,还包括温度在结构上分布多样,对于不同材料温度的传导率不同、线膨胀系数不同等方面。目前科研工作者所建立的模型基本是以某个实际桥梁为背景,所建模型的泛化能力尚未得到广泛验证。在今后的桥梁动态特性研究中,亟需考虑温度分布梯度变化及其温度—模态频率模型,并提高温度—模态频率模型的泛化能力。
[1]张通.温度对大型桥梁模态频率的影响研究[J].武汉理工大学学报,2011,21(7):7-33.
[2]Xia,Y.,Hao,H.,Zanardo,G., et al. A long term vibration monitoring of an RC slab:Temperature and humidity effect.Engineering Structures[C].2006.
[3]叶见曙,贾琳,钱培舒.混凝土箱梁温度分布观测与研究[J].东南大学学报(自然科学版),2002(5):788-793.
[4]JTG D60—2004,公路桥涵设计通用规范[S].
[5]徐赵东,马为乐.结构动力学[M].北京:科学出版社,2007:59-61.
[6]丁幼亮,李爱群,耿方方.温度变化影响下基于神经网络的悬索桥损伤预警方法[J].Journal of Southeast University(English Edition),2010(4):586-590.
[7]邓乃阳,田英杰.数据挖掘中的新方法:支持向量机[M].北京:科学出版社,2004.
[8]樊可清,倪一清,高赞明.大跨度桥梁模态频率识别中的温度影响研究[J].中国公路学报,2006(2):67-73.
[9]邓扬.基于长期监测数据的大跨桥梁结构状态预警与评估方法及其应用[D].南京:东南大学,2010:39.
A review on effects of environmental temperature on dynamic characteristics of bridge structures★
Xia Cheng1Fu Guanglai2Liu Tianqi3
(1.School of Civil Engineering, Southeast University, Nanjing 210018, China;2.State Grid Shandong Electric Power Economic Research Institute, Jinan 250021, China;3.Jiangsu Jingjiang Senior Middle School, Jingjiang 214500, China)
From the changes of material properties caused by the temperature, temperature stress caused by the indeterminate structures, and various distribution of structural temperature, the paper analyzes the mechanism of the temperature on structural influence, and indicates the temperature-model frequency, so it has the prospect for the research on the temperature-model frequency framework.
environmental temperature, bridge structure, model frequency, dynamic property
1009-6825(2016)25-0160-03
2016-06-28★:国家自然科学基金(项目编号:51578140)资助
夏呈(1991- ),男,在读硕士;付光来(1990- ),男,硕士;刘天齐(1999- ),男,在校学生
U441
A
