基于遗传算法的轨道交通与常规公交线路优化方案

陈　丹，徐文远

(1.东北林业大学 土木工程学院, 黑龙江 哈尔滨　150040； 2.北京市市政工程设计研究总院有限公司， 北京　100082)



·信息科学·

基于遗传算法的轨道交通与常规公交线路优化方案

陈丹1，2，徐文远1

(1.东北林业大学 土木工程学院, 黑龙江 哈尔滨150040； 2.北京市市政工程设计研究总院有限公司， 北京100082)

为全面提高公共交通的整体效益,充分发挥轨道交通在公共交通中的骨干作用,需要对轨道交通影响范围内的常规公交线网进行优化调整。文中结合城市轨道交通与常规公交相互协调的交通特点,提出基于“遗传算法”的常规公交线网优化模型。并结合实例，对哈尔滨市地铁1号线的常规公交线网进行调整，选出最佳方案。

轨道交通;常规公交;遗传算法;线路调整

随着轨道交通的兴建,出现了常规公交与轨道交通之间恶性竞争、资源浪费等现象,而轨道交通建成后很难再调整,因此开展基于轨道交通的现有公交线路优化工作已迫在眉睫。

国外在二十世纪七十年代初就开始了各种交通方式间衔接问题的研究,Lampkin等人[1]用乘客舒适度和出行时间作为主要指标,建立交通线网优化模型。基于出行分配、路径规划、行车间隔,Cedar和Wilson提出了线网设计的三阶段法,Martins等人研究启发式算法在线网优化中的应用[2]。Kuah等人考虑接驳公交社会效益和系统效益,建立了系统收益分析模型[3]。国内相关研究较晚,王炜教授等人以换乘客流最小和运量最大为目标,提出“逐条布设、优化成网”的方法[4]。蒋冰蕾等人建立了以换乘站点周转量极大值和换乘线接运效率极大值为目标的目标优化搜索算法[5]。韩传峰,胡志伟等人基于平均换乘次数,通过数学模型来研究线网拓扑结构,并对系统系性能进行评价[6]。这类算法大都通过建立评价指标或者迭代运算实现。综合评价等证优类方法存在针对性不足,效率低下,优化结果不理想等特点;而一般的迭代运算方法非常容易陷入局部最优的陷阱，从而出现“死循环”现象,使迭代无法进行,导致优化方案不够理想。遗传算法属于进化算法，用该方法求出优化问题的最优解能很好避免传统算法的缺点,具有明显的优越性。

常规遗传算法在迭代过程中,交叉和变异概率常取一个固定值，这是运算性能下降的重要因素。遗传运算初期稍大的交叉概率能提高搜索效率,后期其值较小能减少理想基因的损坏;而变异概率则是个体性能越好，其值越小。本文给出了交叉变异概率的自适应公式,在运算过程中采用自适应交叉和变异概率值,对改进传统遗传算法性能和提高优化求解效能具有重要意义。

1　基于轨道交通的常规公交调整

1.1调整目标

调整目标[7]如下:

1)优化公交线网布局,增加轨道交通客流量，缩短成本回收期;

2)加强公交子系统间的合作,提高系统出行效率,提升系统运营效益;

3)降低各交通出行方式间的不良竞争,减少资源浪费。

1.2研究思路

根据优化目标,以路网和出行相关数据为基础,确定目标函数及约束条件。建立初始路网和理想模型,用遗传算法在值域内进行若干次迭算,当满足终止条件时停止跌算,得到理想解,得出线路优化方案。

1.3模型的建立

1.3.1目标函数本文以乘客公交出行总时间为目标函数，其最小值即为最优线路方案。轨道交通线路确定后就不能再轻易改变,在计算时将其算作一条固定的线路。

以线路各OD点间的搭配方式为元素构成集合,由集合构成搭配矩阵X,用r表示搭配方式、s表示搭配方式间的第s最短路,r，s分别构成矩阵的行和列。xrs=1表示搭配方式r的第s最短路上存在公交线路,xrs=0表示搭配方式r的第s最短路上不存在公交线路。出行者总出行时间[8]T为

(1)

其中,fij为小区i,j间的公交客流量,Tij(X)为当前公交网络条件下小区i,j间的公交出行时间。

(2)

其中,lij为小区i,j之间公交线路距离,Tr为步行时间,Tw为候车时间,n为换乘次数,Th为一次换乘时间,v为公交或轨道交通行驶速度(一般采用平均速度)。

常规公交的平均候车时间Tw为

(3)

其中,L为公交线路总长度,n为公交车辆数。

当路网中公交中间站点的运输服务能力不能满足公共交通出行客流需求时,应设起讫站点(OD点)。起讫站点客流运输能力与高峰小时满载率、高峰小时发车间隔等多个因素有关,其计算公式为

(4)其中,C′为起讫站点运输能力,R为公交车辆额定载客数,r为高峰小时满载率,t为高峰小时发车间隔,

1.3.2约束条件根据《城市道路交通规划设计规范》GB 50220-1995，确定线路非直线系数和线长为公交线路优化模型的约束条件[9]。

非直线系数的公式为

(5)

其中,aws为搭配w间第s最短路非直线系数,lws为搭配w间第s最短路的长度,dws为搭配w的直线距离。

建立线网优化模型为

s.t. 8 km≤lws≤12 km，aws≤1.4。

(6)

其中,lws为公交线路长度,aws为非直线系数。

1.3.3遗传算法概述遗传算法属于全局性概率搜索算法[10]。首先需确定初始解,然后不断迭代逐步优化当前解,直到得出理想解时停止运算。迭代运算是遗传算法的重要环节,其采用了自然选择和有性繁殖的原理,在继承父代优良基因的基础上,生成性能更好的子代解。运算方式如下:

图1　遗传算法示意图Fig.1　Sketch Map of genetic algorithm

2　遗传算法应用

2.1遗传编码

模型的解空间由若干个公交网络构成,每个公交网络都包含若干条公交线路,每条公交线路又连接若干个公交起讫站点。

假设某公交网路包含10个交通小区,每个交通小区分别用阿拉伯数字2～11表示,其中2、3、6、8、11号小区需设起讫站点,其余为中转站点,则路网公交线路情况可用下式表示:

D=(h2_3,h2_6,h2_8,h2_11,h3_6,h3_8,h3_11,h6_8,h6_11,h8_11)。

(7)

其中,D是公交网络,hi_j是小区i,j间的公交线路。

所有公交线路均包含在该网络中,但并非所有起讫点配对方式间都有公交线路连接。采用二进制编码方式,1表示两起讫点间有公交线路连接,0表示两起讫点间无公交线路连接。采用式(7)的配对顺序，则

D=(1,0,0,1,1,0,0,0,1,0)。

(8)

式(8)表明,具有公交线路相连的起讫站为:2站与3站、2站与11站、3站与6站和6站与11站。可行线路必须满足式(6),由式(5)和(6)得:

lmin≤lij≤min(1.4dij,lmax)。

(9)

其中,lmin和lmax分别为线路最小和最大长度,lij为站点i,j间线路长度,dij为站点i,j间直线距离。

满足式(9)的线路集构成了问题的可行解集。计算时采用k-最短路法[11]，在约束式(4)的基础上得出全部第k-最短路的解集为

H(2_11,1)=(1,3,5,7,9,10),

(10)

H(2_11,3)=(1,2,4,5,6,8,9,10)。

(11)

H(2_11,1)表示2站与11站间的第一最短路径,H(2_11,3)表示2站与11站间的第三最短路径。求出满足条件的所有最短路:

D=(0,2,0,3,0,0,0,0,0,0)。

(12)

表明所有站点中仅2站与6站、2站与11站间存在公交线路，同时也表示2站与6站间的公交线路是第2最短路,2站与11站间的公交线路是第3最短路。此时路网中并未包含轨道交通线路,因此,还需在路网中添加轨道交通线路。设研究路网中仅存在一条轨道交通线路,其值固定为1，放在编码的末位。最终编码为

D=(0,2,0,3,0,0,0,0,0,0,1)。

(13)

2.2变化算子

上一代解集中好的起讫点配对方式和优良的公交线路均通过交叉运算遗传给了下一代解集。在进行交叉运算时,采用单点式交叉运算,对于如下的父本

D1=(1,0,0,2,|0,0,4,0,3,1),

(14)

D2=(0,2,1,0,|0,3,0,1,0,1)。

(15)

交叉点的确定采用随机方式,假设在第4,5位编码之间设置交叉点。交叉后生成新个体为

(16)

(17)

这样父体的部分起讫点配对方式及公交线路就遗传给了子代,而轨道交通部分则未发生变化。

变异运算,采用随机变化的方式，即在低概率下,随机选取子代中一种配对方式,并随机赋值。轨道交通,不进行变异运算。

这样就得到满足非直线系数和线长约束的子代解,对于不在公交线网内的站点,视为不可行解而淘汰。

交叉和变异概率对迭代结果的影响十分严重，交叉概率pc的取值范围一般为0.40～0.99，变异概率pm的取值范围为0.001～0.1。前部分运算希望交叉概率稍微偏大,这样能够使算法的搜索功能提高;在后部分运算时，使其值偏小能够减少对理想基因的损坏,使收敛速度提高。对于适应性高、性能优良的个体，希望其变异概率越小越好,对于适应度低、不好的个体，则希望其有较大的变异。用自适应法对二者取值，

(18)

其中，

(19)

(20)

(21)

其中，

(22)

2.3适应度函数

适应度函数采用式(1)～(6)。确定线路的优先等级为:二次换乘<一次换乘<直达线路。进行客流量分配时,轨道交通作为一条固定不变的线路参与其中。当优先级相同，有多个选择路线时,按出行效用进行选择,使用Logit模型[12]计算选取某路线的概率

(23)

其中,Rk为k号出行路径的交通阻抗,R为出行路径交通阻抗均值,θ为分配参数,m为出行路径数量。

Rk=CTk+Pk。

(24)

其中,C为时间价值,Tk为路径出行时间,Pk为出行票价。

Tk的计算同式(2),由式(2),(23)和(24)得出各OD点间的出行者在各个路径上的出行时间及出行量。进一步可以得出公交系统出行的总时间[13],也是研究模型的适应度函数值。

2.4选择算子

选择运算方法较多,在具体设计时需根据问题实际情况和规模大小综合确定。确定性选择运算[14]方式常常应用于路网规模较大的情况。而随机性选择运算方式(如轮盘赌法)，则常常应用于路网中线路或站点较少的情况。

3　实例分析

哈尔滨市地铁1号线南起哈南站，北至哈东站,途经18个站点,全长27.3km。最高运行速度为80km/h,平均速度为30.17km/h。额定载客容量和日均载客量分别为1 470人和14.65万人次。根据《城市道路交通规划设计规范》，地铁线路的直接吸引范围[15]为轨道线路两侧500m带状范围。本例选取西大桥站—博物馆站—烟厂站路段进行研究。路网如图2所示，路网中数字为公交车行驶时间(min)。其中地铁1号线线路为图中虚线部分(F-M-S),公交车和地铁的平均运行速度分别为15km/h和30km/h。OD需求矩阵如表1所示。

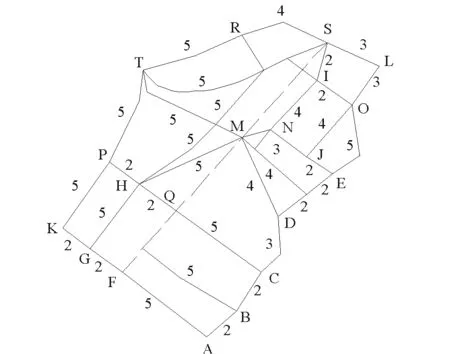
A 和兴路; B 文政街; C 文昌街;D 文明街;E 果戈理大街;F 西大桥;G 通达街; H 抚顺街; I 龙江街;J 人和街; K 民安街; L 鼎新三道街;M 博物馆; N 花园街; O 大成街图2　算例路网图Fig.2　Network map of example road

算例中小区A，E，M，P，S处设置起讫站点,由于F-S间存在地铁线路,故不再将其进行起讫站点配对分析。对各配对方式的线长和非直线系数情况进行检测,结果见表2。

取公交线路的最大长度、最小长度分别为6km，2km,模式EM不满足式(4)，而被淘汰。地铁线路FS，FM段长度分别为4.5km，2.5km,平均速度30km/h,则FM，MS间的行驶时间分别为5min，4min。出行者根据效用选乘地铁或常规公交,客流分配方式优先等级为:2次换乘<1次换乘<直达线路。当存在多条换乘情况相同的线路时,乘客选中某线路的概率按下式计算，

(25)

其中,ti为i线路的行驶时间，A为同一优先等级下的所有可选线路。

使用Matlab软件[16]进行编程。忽略乘客公共交通出行的步行时间,换乘平均耗时取3min。假设案例路网中共有公交车20辆，种群的规模初步定为30,初始以0.95的交叉概率进行交叉运算，以0.10的变异概率进行变异运算,随着迭代进行，根据式(18)～(22)确定其相应值。初始种群采用随机方式生成,进行选择运算时,选择方法采用轮盘赌法,反复迭代20次。程序在相同条件下运行5次,最后取5次结果的平均值如图3所示，表3为得出的优化方案。

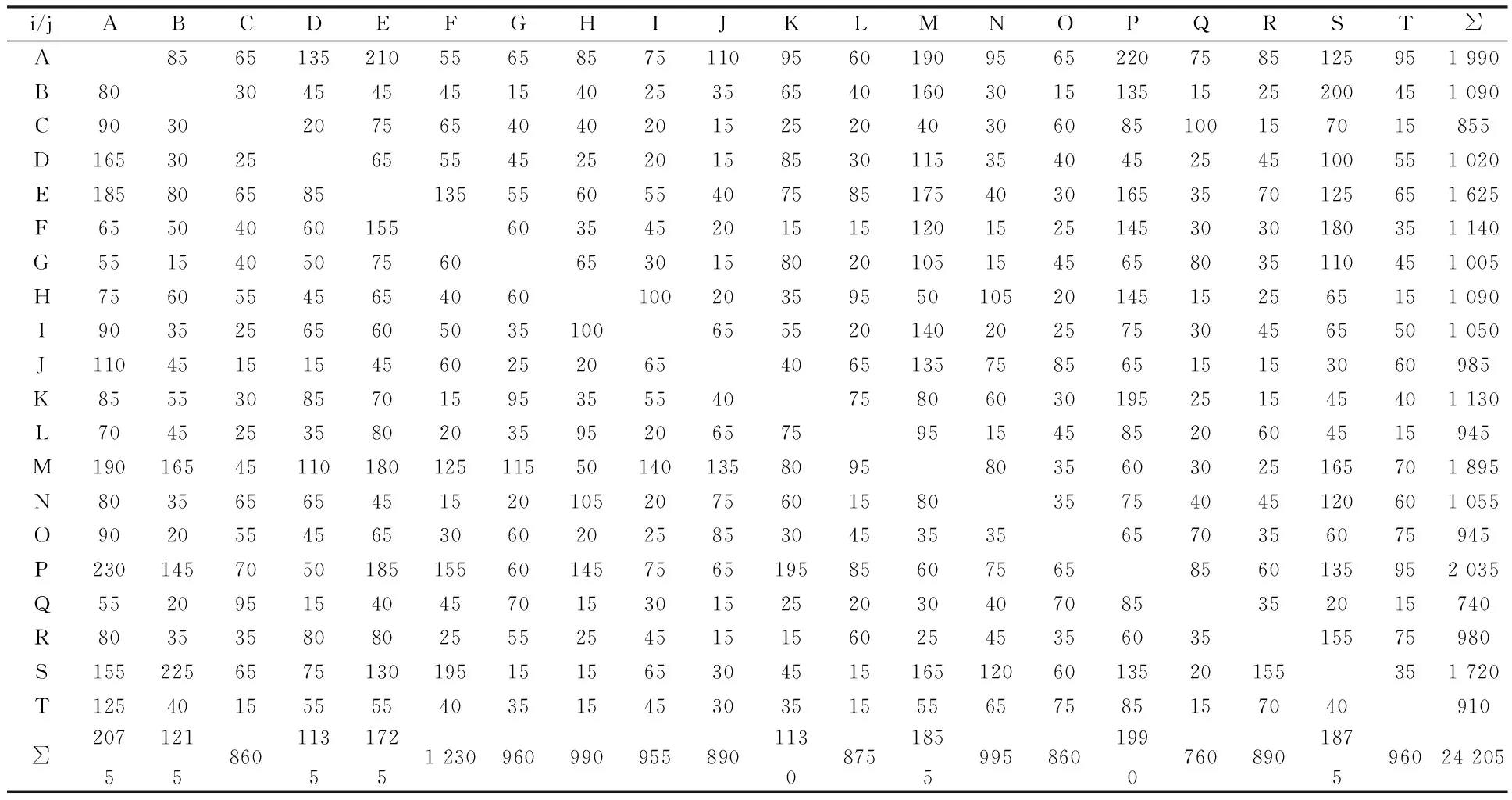
表1　公共交通需求OD矩阵表

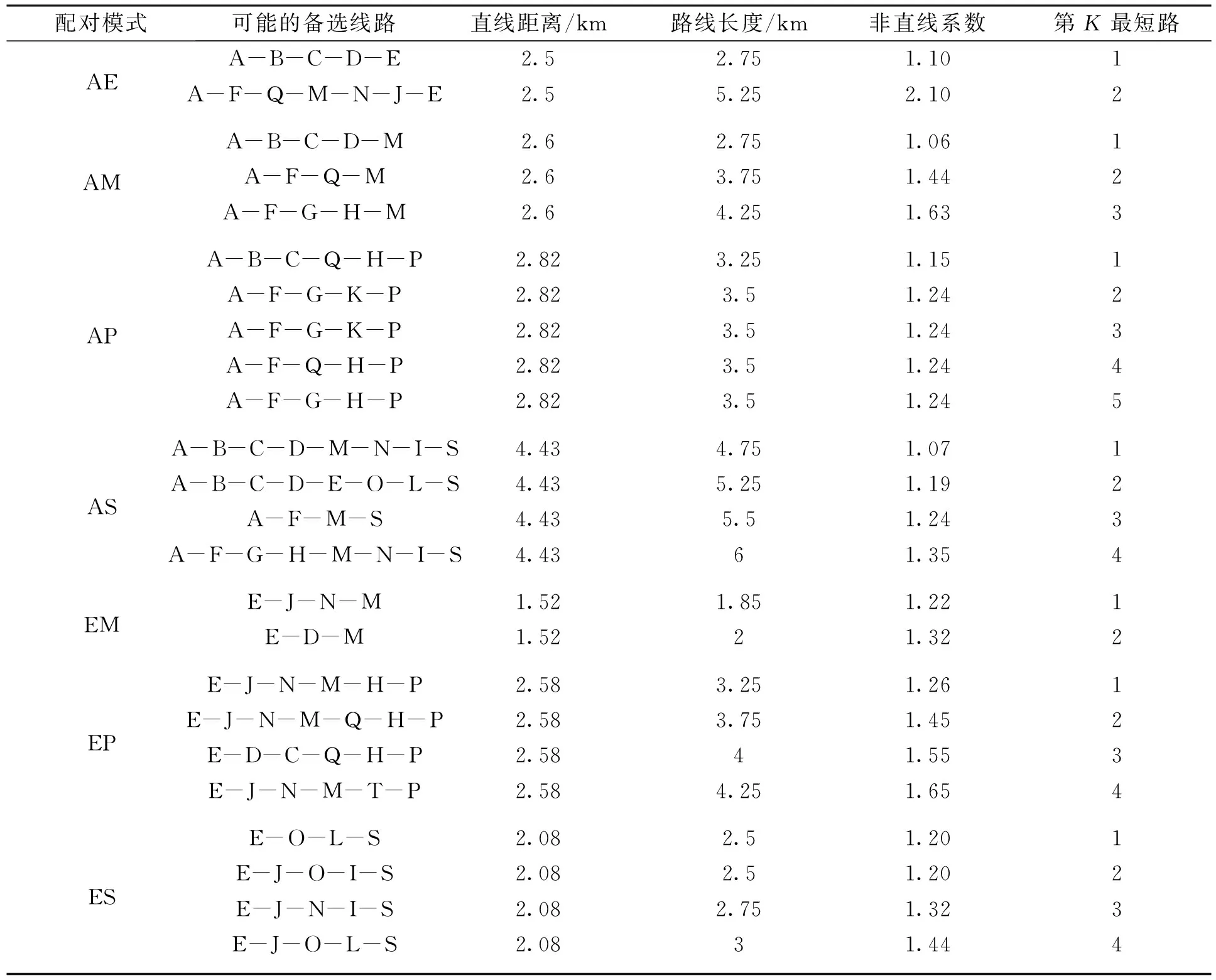
表2　小区现状配对情况表

续表2

配对模式可能的备选线路直线距离/km路线长度/km非直线系数第K最短路MPM-Q-H-P2.12.251.071M-T-P2.12.51.192P-H-M-S2.823.51.241P-T-R-S2.823.51.242P-H-Q-M-N-I-S2.8241.423

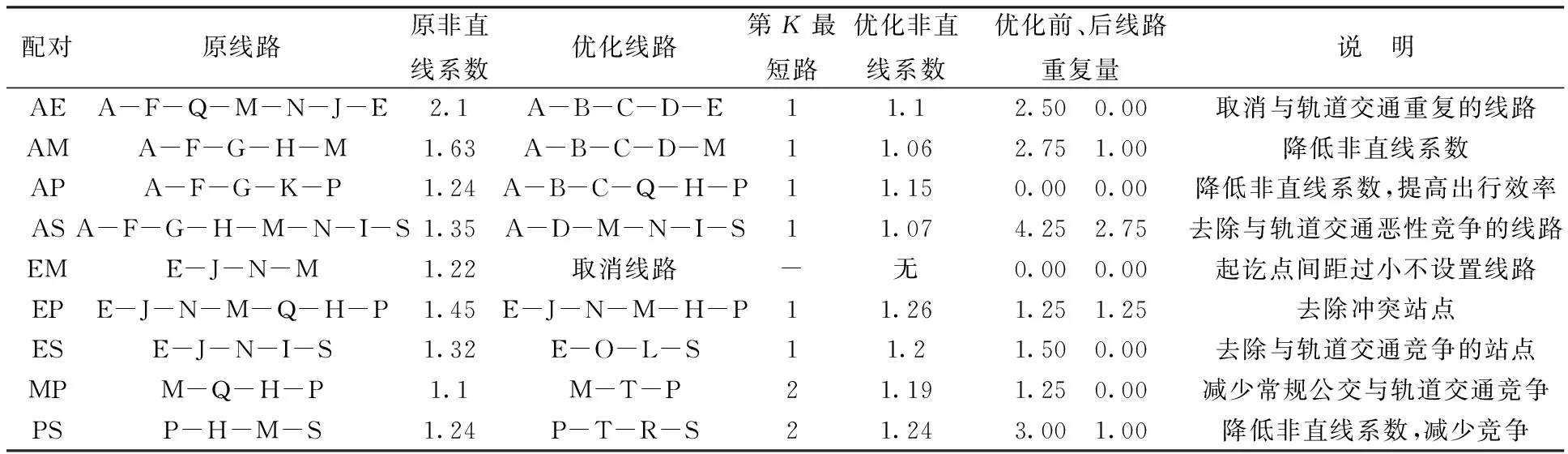
表3　公交线路优化方案

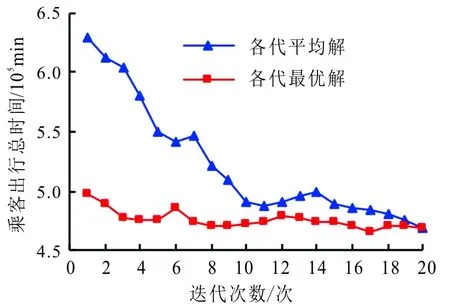
图3　遗传算法收敛过程Fig.3　Convergence process of genetic algorithm

进行线路方案优化后,路网中乘客出行总时间为469 758min,乘客平均出行耗时19.41min，小于25min,符合《城市道路交通规划设计规范》中居民单程最大出行时耗的要求。路网中各公交线路的非直线系数均小于1.4,满足城市公交线路非直线系数不得大于1.4的要求。

线路重复系数[17]α应该越小越好,计算公式如下

(26)

其中,G总为轨道交通线路、线网的总长度，Li为地铁影响范围内的常规公交线路i与地铁线路相平行的距离，i为第i条与地铁平行的线路，N为研究范围内与地铁平行的线路总数。

算例中地铁线路长度为7.0km,调整前线路重复距离为16.50km,此时计算线路重复系数为2.36;调整后重复距离为6.0km,此时计算线路重复系数为0.86,大大减少了常规公交与地铁间的恶性竞争,线路优化方案取得了良好的效果。

4　结　语

本文立足于遗传算法在优化问题中的优点,以研究范围内乘客出行时耗最小为线网优化的目标函数,以公交线路长度和非直线系数为约束条件,介绍了遗传算法在基于轨道交通的现有公交线网优化工作中的应用,弥补了一般迭代算法容易陷入局部最优陷阱或出现“死循环”现象而导致优化方案不尽合理的缺点,得到了较理想的优化方案。结合实际，对哈尔滨市地铁1号线影响范围内的现有公交线路进行优化调整,取得了很好的效果。说明运用遗传算法能科学、合理、便捷地对常规公交线路进行优化调整,对提高公交系统运行效率、降低资源浪费具有重要意义。

[1]LAMPKIN W, SAALMANS P D. The design of routes, service frequencies, and schedules for a municipal bus undertaking: A case study [J]. Operation Researeh Quart,1998,51(3): 41-42.

[2]CEDER A, WILSON N H M. Bus network design[J]. Transportation Research Part B: Methodological, 1986, 20(4): 331-344.

[3]MARTINS C L, PATO M V. Seareh strategies for the feeder bus network design problem[J] European Journal of Operation Researeh, 1998, 106(2): 425-440.

[4]王炜.实用公交线网规划方法研究[J].东南大学学报(自然科学版),1990,20(4):81-88.

[5]蒋冰蕾，孙爱充.城市快速轨道交通接运公交路线网规划[J].系统工程理论与实践,1998(3):130-134.

[6]韩传峰,胡志伟.城市公交路网性能评估的网络图方法[J].系统工程,2003, 21(3):58-61.

[7]吴娇蓉,汪煜,刘莹.城市轨道交通各发展阶段的运行特征及在公交系统中的作用[J].城市轨道交通研究,2007(6):9-11.

[8]林伯梁,杨富社,李鹏.基于出行费用最小化的公交网络优化模型[J].中国公路学报,1999,12(1):79-83.

[9]国家质检总局(GN-GB).GB 50220-1995城市道路交通规划设计规范[S].北京：人民交通出版社，1995.

[10] 韩瑞锋.遗传算法原理与应用实例[M].北京:兵器工业出版社,2010.

[11] 郑建斌,杨小曼,刘辉,等.遗传小波神经网络用于极谱信号的流噪[J].西北大学学报(自然科学版), 2002,32(5):447-450.

[12] KALOUPTSIDIS N, PSARAKI V. Approximations of choice probabilities in mixed logit models [J]. European Journal of Operational Research,2010,200(2):529-535.

[13] NAYEEM M A, RAHMAN M K, RAHMAN M S. Transit network design by genetic algorithm with elitism [J]. Transportation Research Part C: Emerging Technologies, 2014, 46: 30-45.

[14] 敖友云,迟洪钦.基于(μ+λ)选择策略的多目标优化分段遗传算法[J].计算机工程与科学，2006,28(9):91-93.

[15] 吴休鹏.武汉市轨道交通二号线接运公交线网优化研究[D].武汉:武汉理工大学,2011.

[16] 虞蕾,赵红,赵宗涛.一种基于遗传算法的航迹优化方法[J].西北大学学报(自然科学版),2006,36(2):205-208.

[17] 王卫平.常规公交与城市轨道交通衔接理论方法与评价研究[D].广州:华南理工大学,2011.

(编辑李静)

Optimization scheme of rail transportation and conventional bus lines based on genetic algorithm

CHEN Dan1，2, XU Wen-yuan1

(1.School of Civil Engineering, Northeast Forestry University, Harbin 1500140, China；2.Beijing Municipal Engineering Design & Research Institute Co.,Ltd., Beijing 100082, China)

In order to enhance the overall efficiency of public transportation, give full play to the backbone role of rail transit in public transportation, adjust the regular bus network within the scope of the influence of rail transit, in this paper, combined with the characteristics of regular bus and new rail transit, the optimization model is put forward based on the "genetic algorithm". And using genetic algorithm to adjust the regular bus network around the Harbin city metro line, the best scheme is selected.

rail transit; conventional transit; genetic algorithm; circuit conditioning

2015-08-17

黑龙江省交通运输厅重点科技基金资助项目(2011TZD037)

陈丹，男，四川资阳人，从事交通运输、计算机应用技术研究。

U491

A

10.16152/j.cnki.xdxbzr.2016-03-011