参数未知的超混沌系统的反同步与参数辨识

吴淑花，容旭巍，刘振永

(石家庄学院 物理与电气信息工程系,河北 石家庄　050035)



·数理科学·

参数未知的超混沌系统的反同步与参数辨识

吴淑花，容旭巍，刘振永

(石家庄学院 物理与电气信息工程系,河北 石家庄050035)

基于混沌同步的主动控制法,提出反对称结构的直接构造法，利用该方法设计了反同步控制器和参数追踪规则,构建了反同步控制器的电路实验,实现了参数未知的超混沌耦合发电机系统的反同步与未知参数的辨识。数值模拟和电路仿真结果证明了该方法的有效性。

超混沌耦合发电机系统;反对称结构;反同步;参数辨识;电路实验

1990年,Pecora和Carroll[1]提出的驱动-响应同步方法,其开创性的工作极大地推动了混沌同步的研究。在随后的十余年里,人们发现了各种不同类型的同步现象,如广义同步[2]、相同步[3]、延迟同步[4]、射影同步[5]等。最近,人们研究了混沌系统的反同步现象,即处于同步的两个混沌系统,状态变量的绝对值相同，但符号相反。目前,实现混沌同步或反同步的方法主要有主动控制法[6]、自适应控制法[7-8]、滑膜控制法[8-9]、有限时间同步法[10-11]等。以往文献主要是围绕参数已知的低维混沌系统的同步研究,而参数不确定的高维混沌系统的反同步研究较少。与低维混沌系统相比,高维混沌系统具有更加复杂的动态行为和更广泛的应用,所以,近年来超混沌系统的同步研究逐渐受到关注[6,10,12]。

文献[7,13-15] 分别采用不同的有效措施对耦合发电机系统进行有效控制;文献[16]在[15]的基础上构建了超混沌耦合发电机系统,利用非线性控制器实现了超混沌耦合发电机系统的自结构和异结构同步。然而,上述方法对于参数未知的超混沌耦合发电机系统的同步控制是无法实现的。主动控制法虽具有简单有效且不需要确定Lyapunov函数的优点,但构造控制器的盲目性使得人们较少使用。部分文献中用此方法实现了参数已知的混沌系统的同步或反同步[6,8]。为避免主动控制法的盲目性,本文对主动控制法做了进一步的改进,引入反对称结构的反同步直接构造法,为响应系统设计了适当的控制器;在上述方案设计的基础上,设计了未知参数的追踪规则;构建了超混沌耦合发电机系统的反同步电路和参数辨识电路,实现了不确定参数的超混沌耦合发电机系统的反同步和未知参数的辨识。数值模拟和电路仿真的结果具有高度的一致性,证实了这种同步方案的有效性。

1　问题描述与系统模型

考虑混沌系统由以下状态方程描述

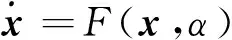
(1)

式中,x∈Rn为系统的状态向量,α为系统参数。构造如下的响应系统

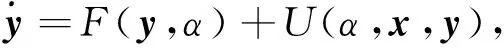
(2)

这里,U(α,x,y)为控制输入。定义系统(1)和系统(2)的反同步误差为e=x+y,则由式(1)和式(2)可得误差系统为

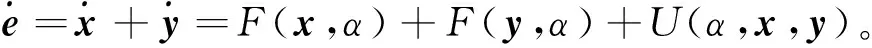
(3)

eT[F(x,α)+F(y,α)+U(α,x,y)]。

(4)

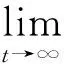
从定义1可以看出,系统(1)和系统(2)的反同步问题,已转化为误差系统(3)的状态在原点的渐进稳定性问题。

2006年王兴元和武相军提出了变形耦合发电机系统[15],在此基础上文献[16]提出了超混沌耦合发电机系统

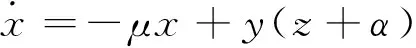
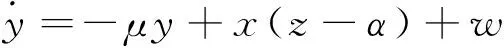
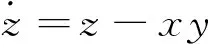
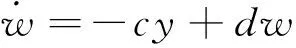
(5)

这里x,y,z和w是系统的状态变量,μ,α,c,d为参数。当μ=2,α=3,c=2,d=1时,系统(5)为超混沌系统。图1为系统(5)的超混沌吸引子。

以超混沌耦合发电机系统为驱动系统,其数学模型可写为

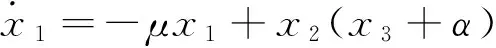
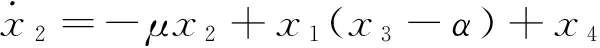
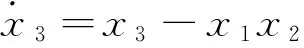
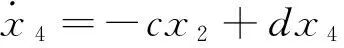
(6)

其中,x1,x2,x3,x4为状态变量,系统参数的取值分别为μ=2,α=3,c=2,d=1时,系统(6)处于超混沌状态。构造下面的响应系统,其数学模型为

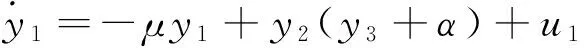
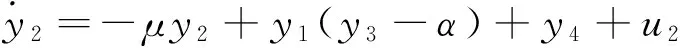
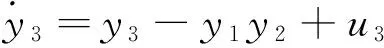
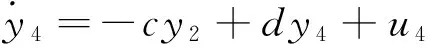
(7)

其中，y1,y2,y3,y4为状态变量，系统参数μ,α,c,d的取值同式(6)相同。令反同步误差ei=yi+xi(i=1,2,3,4)，得到误差系统

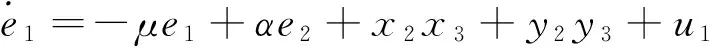
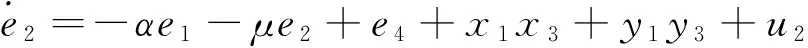
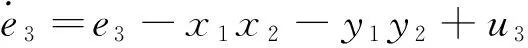
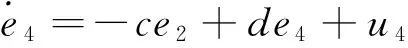
(8)

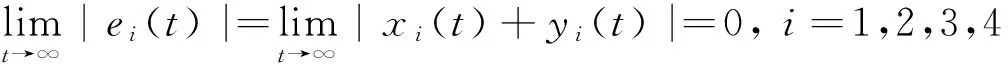
从定义2可以看出,超混沌系统(6)和(7)的反同步问题,已转化为误差系统(8)的状态在原点的渐进稳定性问题。

2　参数未知的超混沌耦合发电机系统的反同步

2.1反同步控制器的设计

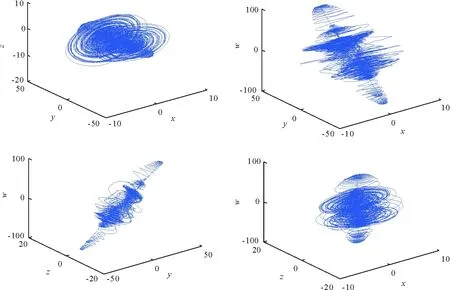
图1　系统(5)的超混沌吸引子Fig.1　The hyperchaotic attractors of (5)

定理1考虑如下的非线性系统

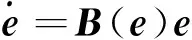
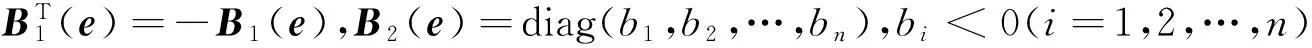
由定义2和定理构造如下的控制器，

u1=-x2x3-y2y3,

u2=-x1x3-y1y3,

u3=-2e3+x1x2+y1y2,

u4=(c-1)e2-(1+d)e4。

(9)

在驱动系统(6)的基础上,构造如下参数未知的响应系统，

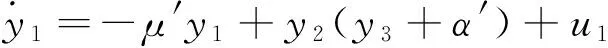
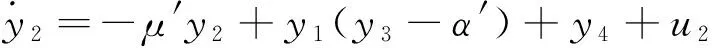
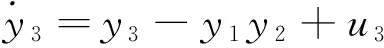
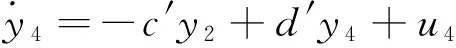
(10)

式中μ′,α′,c′和d′是在驱动系统(6)与响应系统(10)反同步过程中需要辨识的未知参数。选择式子(9)所示的控制器，未知参数的追踪规则为

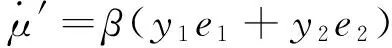
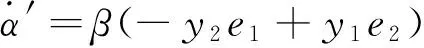
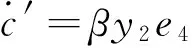
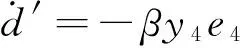
(11)

β为主动增益常数，改变其大小可以调节参数辨识的过程。

2.2数值模拟

通过数值模拟反同步的有效性和未知参数的辨识过程,采用四阶Runge-Kutta法求解方程(6)和(10)。驱动系统参数的取值分别为μ=2,α=3,c=2,d=1,驱动与响应系统状态变量的初始值分别选取经x(0)=[10，-1，20，-10],y(0)=[6，7，8，9], 响应系统(10)未知参数的初始值分别取1，2，-3，-4，主动增益常数取值β=1,模拟结果如图2，3，4，5所示。

图2为超混沌耦合发电机系统(6)与参数未知的响应系统(10)在相空间中的轨迹及其状态曲线。图上可以看见,相轨迹的投影和状态曲线是反对称的,说明式(9)给出的控制器使两个系统达到了反同步。图3为超混沌耦合发电机系统的未知参数的辨识过程。由图可见,随着t的增加,未知参数μ′,α′,c′,d′的值渐近稳定在常数2,3,2和1上,适当减小β的取值,可以缩短未知参数的辨识过程。可见，利用式(11)给出的参数追踪规则，能够在实现系统(6)和系统(10)反同步的同时，辨识出响应系统的未知参数。

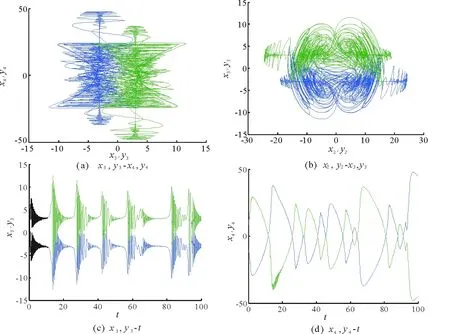
图2　超混沌耦合发电机系统反同步图Fig.2　Anti-synchronization of hyperchaotic coupled dynamos system

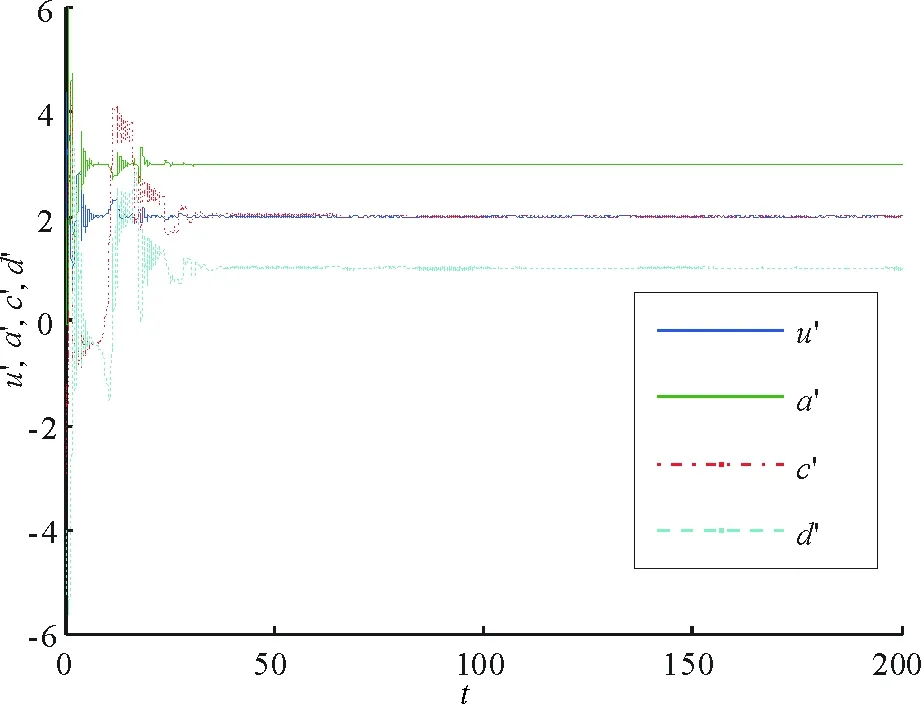
图3　响应系统(10)的未知参数辨识过程Fig.3　Parameters identification on the responser (10) with uncertain parameters

2.3电路设计

应用Multisim软件建立电路模型,主要由乘法器AD633、运算放大器LF353、线性电阻和电容构建而成。运算放大器的供电电源采用±12V双电源供电,为了可靠不失真地完成电路的仿真,把系统的输出电压调小到了原来的1/10,所以乘法器的增益设为0.1。根据电路原理及电路中各个元件特性,设计驱动系统(6)的电路原理图(如图4(a)所示);加入反同步控制器(9)后设计了参数未知的响应系统(10)的电路原理图(如图4(b)所示);按照未知参数的追踪规则(11)设计了图4(c)的电路原理图。

2.4电路仿真

利用Multisim软件分别对电路4进行仿真,分别得到混沌吸引子和两个系统解的振荡曲线。如图5(a)～(d)所示,可以观察到它们的相图和时序图是对称的,与数值模拟得到的图2具有高度的一致性。图5(e)～(h)是对电路4(a)和图4(b)仿真的反同步图像,进一步说明系统(6)和系统(10)确实达到了反同步。

如图6是电路图4(c)的仿真结果,图中显示了4个估计参数随时间的演化图,从图中可以判断，估计参数μ′，α′，c′，d′时域的稳态值分别为2V,3V,2V,1V。所以采用Multisim软件搭建的硬件电路和Matlab软件理论分析仿真的效果一致,说明设计的未知参数追踪规则是正确的。

3　结　论

超混沌系统比混沌系统具有更强的不稳定性,所以实现参数未知的超混沌的反同步具有较多困难,寻找一种既简单又适用的方法就更加困难。本文对主动控制法做了进一步的改进, 提出了反对称结构的直接构造法, 实现了参数未知的超混沌耦合发电机系统的反同步与参数未知的辨识。该方法具有简单易行、计算量小、而且灵活多变等优点。采用Multisim软件搭建了超混沌耦合发电机系统及其未知参数的反同步的硬件电路,电路仿真了反同步相图、时序图和未知参数辨识过程。电路仿真和数值模拟达到了高度的一致性,结果证实了本文所提出的方法的有效性,而且这种方法同样适用于其他参数未知的混沌系统的反同步控制。

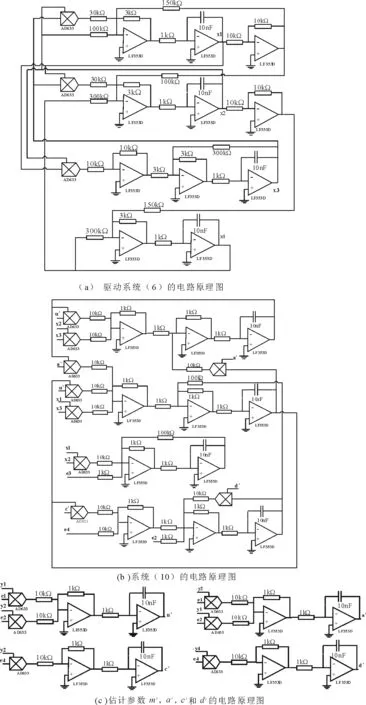
图4　电路原理图Fig.4　Circuit diagrams

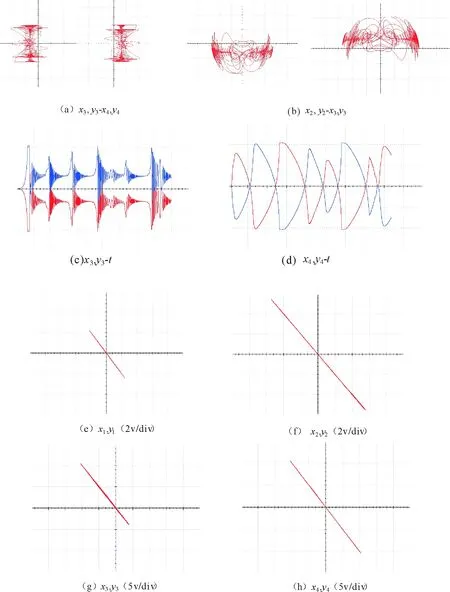
图5　电路图4(a)和(b)的仿真结果Fig.5　Circuit simulation of figure 4(a) and 4(b)

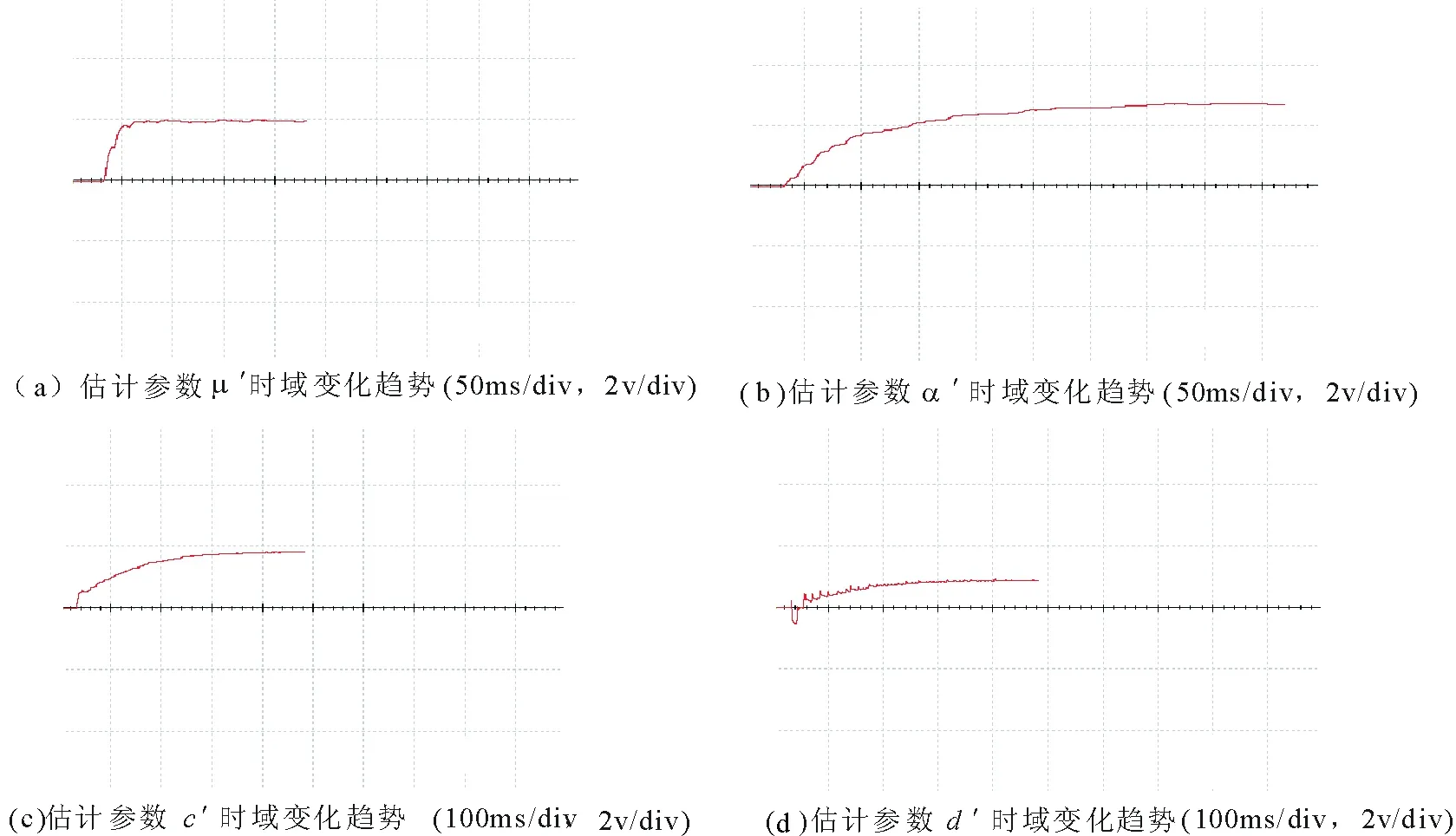
图6　电路图4(c)的仿真结果Fig.6　Circuit simulation of figure 4(c)

[1]PECORALM,CARROLLlTL.Synchronizationinchaoticsystems[J].PhysicalReviewLetter, 1990, 64(8):821-824.

[2]ZHANGR,XUZY,YANGSX,etal.Generalizedsynchronizationviaimpulsivecontrol[J].ChaosSolitons&Fractals, 2008, 38(1): 97-105.

[3]ERJAEEGH,MOMANIS.Phasesynchronizationinfractionaldifferentialchaoticsystems[J].PhysicsLettersA, 2008, 372(14):2350-2354.

[4]CHENY,CHENXX,GUSS.Lagsynchronizationofstructurallynonequivalentchaoticsystemswithtimedelays[J].NonlinearAnalysis:Theory,Methods&Applications, 2007,66(9):1929-1937.

[5]LIGH.Projectivesynchronizationofchaoticsystemusingbacksteppingcontrl[J].ChaosSolitons&Fractals, 2006, 29(2):490-494.

[6]VINCENTUE.Synchronizationofidenticalandnon-identical4-Dchaoticsystemsusingactivecontrol[J].Chaos,Solitons&Fractals,2008,37(4):1065-1075.

[7]El-GOHARYA,YASSENR.Adaptivecontrolandsynchronizationofacoupleddynamosystemwithuncertainparameters[J].Chaos,Solitons&Fractals，2006，29(2)：1085-1094.

[8]刘福才,李俊义,臧秀凤. 基于自适应主动及滑模控制的分数阶超混沌系统异结构反同步[J].物理学报,2011,60(3):030504-10.

[9]李华青,廖晓峰,黄宏宇.基于神经网络和滑模控制的不确定混沌系统同步[J]. 物理学报,2011,60(2)，020512-5.

[10] 赵灵冬，胡建兵，包志华，等.分数阶系统有限时间稳定理论及分数阶超混沌Lorenz系统有限时间同步[J]. 物理学报,2011,60(11):100507-5.

[11] 邵克勇,马永晶,王婷婷，等. 不确定混沌系统的异结构同步[J]. 物理学报,2013,62(2):020514-7.

[12]YANZ，YUP.Hyperchaossynchronizationandcontrolonanewhyperchaoticattractor[J].ChaosSolitons&Fractals，2008,35(2)：333-345.

[13]El-GOHARYA,YASSENR.Chaosandoptimalcontrolofacoupleddynamosystemwithdifferenttimehorizons[J].Chaos,Solitons&Fractals, 2009,41(2)：698-710.

[14]LISH,TIANYP.Globalstabilizationofacoupleddynamosystem[J].Chaos,Solitons&Fractals, 2003,16(5):787-793.

[15] 王兴元,武相军. 变形耦合发电机系统中的混沌控制[J].物理学报,2006,55(10):5083-5093.

[16] 吴淑花,容旭巍,屈双惠，等. 超混沌耦合发电机系统的混沌同步及其电路实现[J]. 四川大学学报(自然科学版),2013,50(3):515-521.

[17] 蔡娜,井元伟,姜囡，等. 超混沌Chen系统和超混沌Loren系统的反同步[J].东北大学学报(自然科学版),2009,30(3):313-317.

(编辑李静)

Anti-synchronization and parameter identification on a hyperchaotic system with uncertain parameters

WU Shu-hua, RONG Xu-wei, LIU Zhen-yong

(Department of Physics and Electrical Information Engineering, Shijiazhuang University, Shijiazhuang 050035， China)

Based on active synchronization control, the anti-symmetric direct construction method is proposed. By using this method, an anti-synchronization controller and a parameter tracking rule are designed, several circuit experiments with an anti-synchronization controller are built. Hyperchaos anti-synchronization and parameters identification on a hyperchaotic coupled dynamos system with uncertain parameters are realized. The results of numerical simulation and circuit simulation verify the effectiveness of the proposed method.

hyperchaotic coupled dynamos system; anti-symmetric structure; anti-synchronization; parameter identification; circuit experiment

2015-03-05

河北省教育科学研究“十二五”规划课题基金资助项目(1412091)；河北省高校科技研究基金资助项目(ZC2016062)；石家庄学院科研基金资助项目(XJPT002, XJTD004)

吴淑花，女，河北石家庄人，副教授，从事非线性研究。

O545

A

10.16152/j.cnki.xdxbzr.2016-03-007