DTM-Adomian-pade求解非线性分数阶微分方程
2016-09-29刘春凤
刘春凤,张 滑
(华北理工大学 理学院,河北 唐山 063000)
·数理科学·
DTM-Adomian-pade求解非线性分数阶微分方程
刘春凤,张滑
(华北理工大学 理学院,河北 唐山063000)
为求解R-L定义下的分数阶非线性微分方程近似解析解,将Adomian多项式、Padé逼近法与R-L微分变换法相结合,提出改进的广义微分变换法。利用Adomian多项式代替方程中的非线性部分,对方程进行广义微分变换法求出其级数解,运用Pade法对其级数解进行逼近。改进的微分变换法不仅计算简单,具有较小的计算量,而且扩大了级数解得收敛范围,具有较高的精度。最后给出数值算例,验证了算法的有效性,为计算R-L分数阶非线性微分方程提出新的计算格式。
R-L微分变换法;非线性分数阶微分方程;Adomian多项式;Padé逼近
分数阶理论是研究任意阶次微积分算子的特性及应用的数学理论。近几十年来,分数阶理论在国内外已经成为一个研究热点,一些科学家已成功将其应用到混沌系统、电磁学、信号处理、黏弹性和遗传性力学、机械工程和机器人控制等方面。研究分数阶方程的解是非常必要的,尤其是非线性问题的分数维方程,而微分变换法为求解分数阶微积分方程的解析解提供了新的数学工具。微分变换法(DTM)最初是由我国学者赵家奎[1]提出的,用于求解电路问题中的微分方程,微分变换法计算量小、精度高,这个方法逐渐被应用到了线性和非线性微积分方程。Ayaz[2]在此基础上推导出了二元函数的微分变换,并将其应用于求解二维偏微分方程的初值问题;Lal[3]等利用此方法分析了力学中自由振动和屈曲的积分方程;Abdulkawi[4]利用微分变换法求解奇异积分方程的初值问题,并得到了很好的结果;Arikoglu和Ozkol[5]在微分变换方法的基础上,建立了求解Caputo导数定义下的分数阶微分方程的广义微分变换法(FDTM),并将其推广应用于求解积分方程和分数阶微积分方程问题;Vineet[6]等利用FDTM求解了二维和三维的分数阶电报方程,为求解复杂的分数维方程提供了一个良好的工具;Corporation[7]把广义微分变换法应用到求解分数阶混沌系统,并和龙格库塔法进行了比较,验证了广义微分变化法的有效性;Matteo[8]把广义微分变换法应用到了分数维方程的边值问题;Abuteen[9]等利用广义微分变化法求解分数阶Bloch系统。
目前,对Caputo分数阶导数定义下的广义微分变换法已经逐渐地被应用到分数维微分方程和积分方程求解中,并得到了很好的结果,而对R-L导数定义下的广义微分变换法研究甚少,本文将Adomian多项式、Pade 逼近法与R-L定义下的微分变换法相结合,提出一种改进的微分变换法。
1 预备知识
(1)
定义2Caputo分数阶导数定义
(2)
分数阶导数的主要性质

(3)
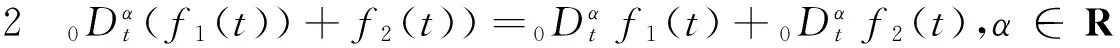
(4)
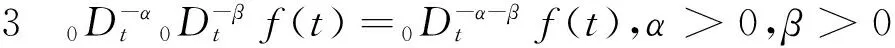
(5)
2 R-L微分变换法
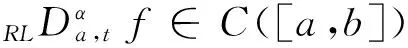
f(x)=[(x-a)1-αf(x)](a+)(x-a)α-1+
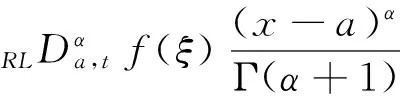
(6)
则式(6)是R-L导数的广义Taylor公式。
根据引理1,设函数f(x)对变量x的k阶导数存在,定义f(x)关于x的k阶导数在点x0处的R-L广义微分变换形式为
(7)
通过微分变换法将f(x)近似表示成如下形式:
(8)
函数的微分变换具有如下基本运算法则:
文献[12]仅讨论了分数阶导数在0<α<1的微分变换,本文在此基础上把R-L广义微分变换法推广到一般形式。
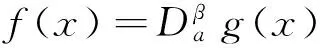
证 明根据定义
Fα(k)=

表1 微分变化法的运算
3 改进的微分变换法
微分变换法求解非线性分数阶微分方程的关键在于非线性项的处理,利用Adomian多项式去等价代换方程的非线性项,减少了计算量,但是所得级数解一般只能在其自变量的初值点附近的子区间内与正确结果相符,而对级数解进行Padé逼近,可以扩大收敛区间,提高收敛精度。将上述方法相结合,提出改进的微分变化法,称为DTM-Adomian-Padé法。
3.1Adomian多项式
首先非线性函数部分由Adomian多项式近似,则
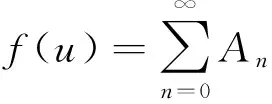
其中An为Adomian多项式(见表2),Adomian多项式的定义如下:
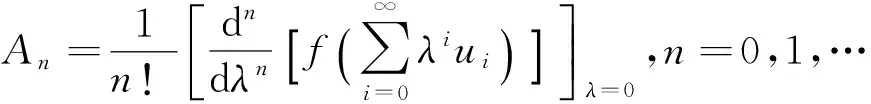

表2 Adomian多项式
对Adomian多项式进行微分变换(见表3)。
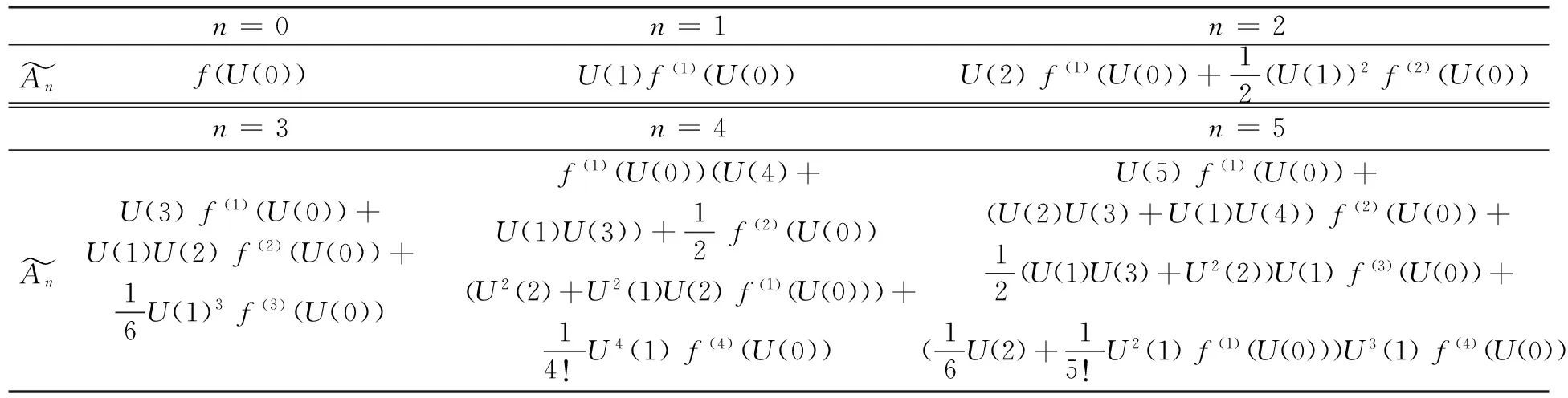
表3 Adomian多项式微分变换
当非线性函数部分为分数阶导数f(u(γ))的形式时,则与含有分数阶导数的函数等价的Adomian多项式为表4。

表4 广义Adomian多项式
由式(8)知,
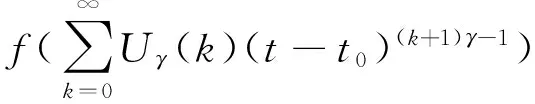
对与分数阶函数等价的Adomian多项式做R-L微分变换(见表5)。

表5 广义Adomian多项式的微分变换
综上所述,Adomian多项式的R-L微分变换归纳为
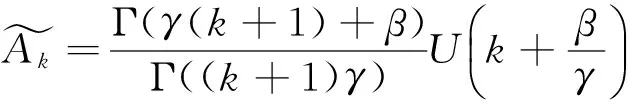
3.2Padé逼近
Padé逼近是一种关于函数值的特殊类型的分式逼近法,是以尽量快的速度与Taylor级数展开式相匹配,逼近效果好。
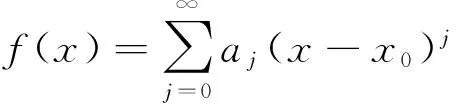
[L/M]=PL(x)/QM(x)。
(9)
其中PL(x)是一个次数最高为L的多项式,QM(x)是一个次数最高为M的多项式。
(10)
(11)
则
(12)
式(12)为函数f(x)的[L/M]阶Padé逼近多项式。
下面给出几个数值算例,验证算法的有效性。
例1Dαy=1+y2,0<α≤1,y(0)=0
(13)
利用Adomian多项式替换式(13)非线性项,并对两边进行微分变换
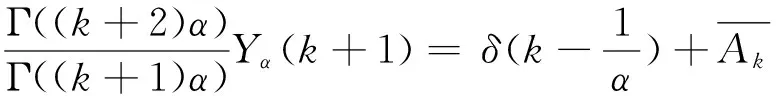
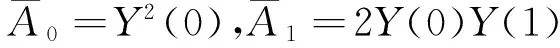
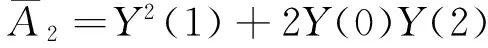
求得式(13)截断级数解
y=1.128 4t0.5+1.2734083125t1.5+
1.300 9t2.5+3.177 5t3.5+…
对级数解使用Padé逼近,则
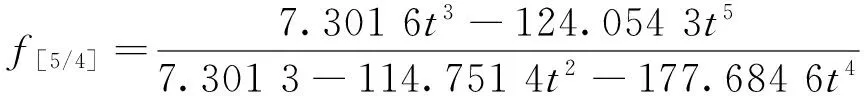
得到式(13)修正级数解
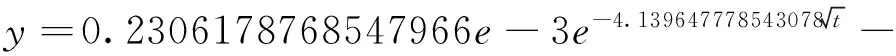
0.6981713665675022
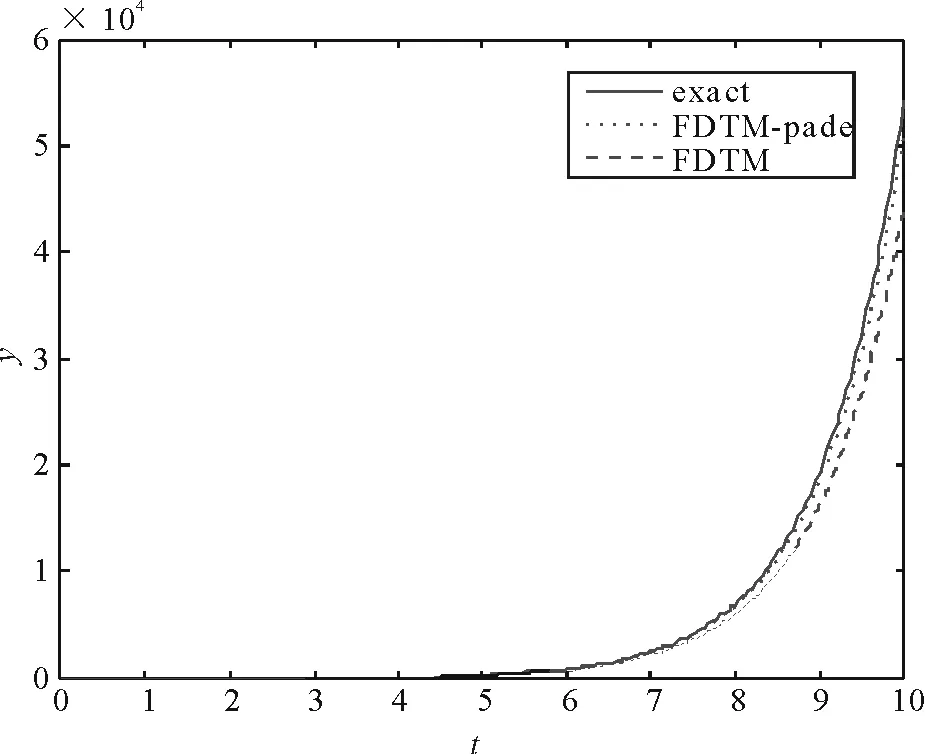
图1 改进的微分变换法,微分变换法与数值解比较图Fig.1 Comparison of the solution by different method
例2D1.75y+y3+y′=0,y(0)=1,y′(0)=0,对上式两边进行微分变换,则
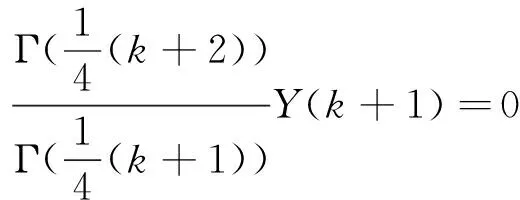
Y(0)=0,Y(1)=0。
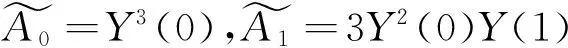
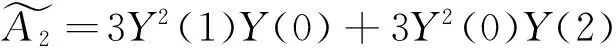
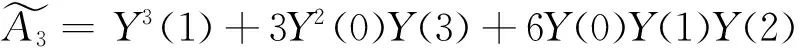
3Y(4)Y2(0)+6Y(0)Y(1)Y(3)+…
得到例2截断级数解
y=1-0.621 8t1.75+0.121 7t3.25+0.086 0t3.5-0.012 7t4.75-0.036 6t5-0.121 7t5.25
对解进行修正,则对上式进行Padé逼近,表2是改进的DTM算法DTM方法和精确解对照表。
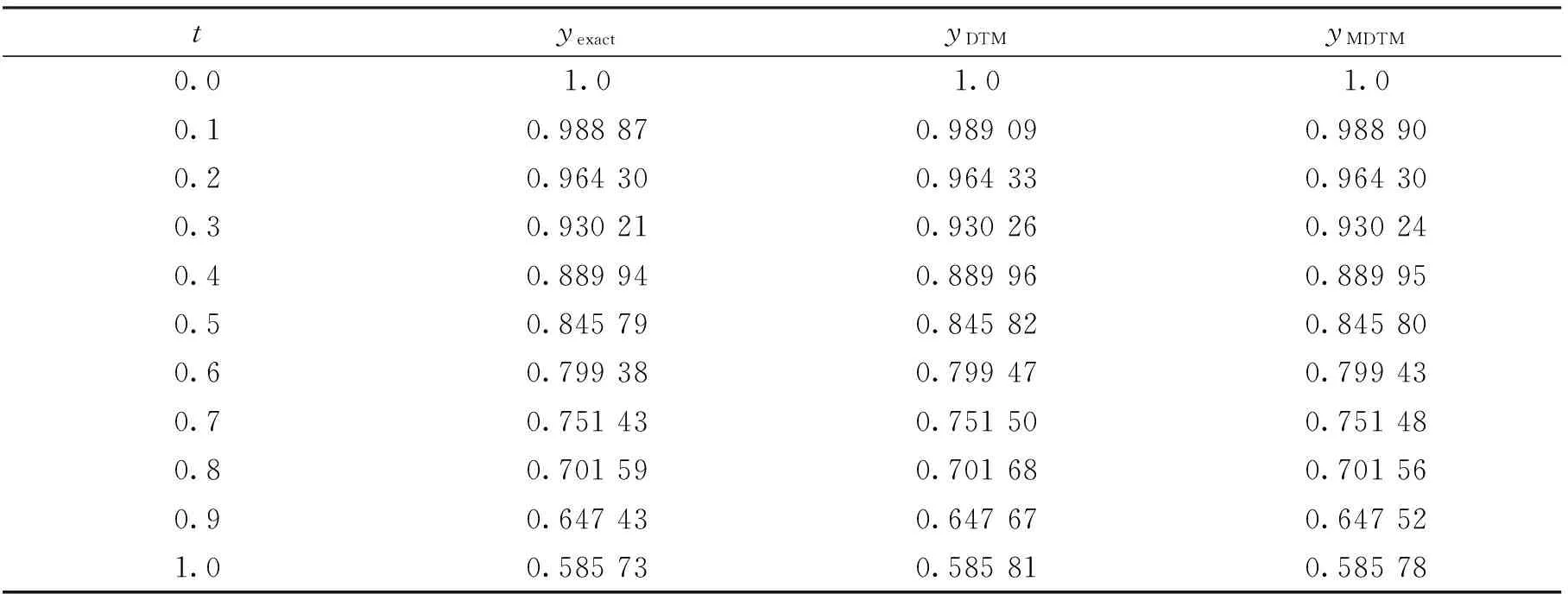
表6 不同算法结果比照表
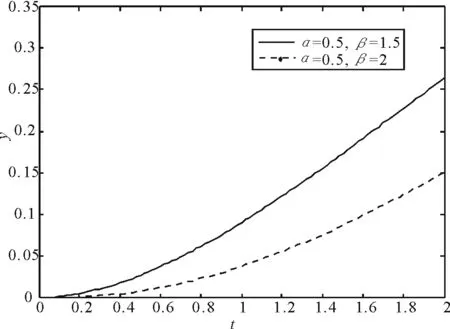
例3Dβy-yDαy-1=0,y(0)=0,y′(0)=0,m-1<β 当β=1.5,α=0.5时,则例3的截断级数解为 y=1.12838t1.5+0.0625t4-0.0458732t6.5+0.00566209t9。 对上式进行Padé逼近,则 f[3/3]=(947967.451431t+970616t2-63198t3)/(6.3198+15099.13273t+36.1426t2+8.615125t3) 得到例3修正级数解 y(t)=a1e-2516.497615944428t+a2e-0.1192027785973775e-2tcos(0.2298730050954942e-t)-a3e-0.1192027785973775e-2tsin(0.2298730050954942e-t)+a4e-12i(-285100139160575.3e-0.1192027785973775e-2t cos(0.2298730050954942e-t)+ a5e-0.1192027785973775e-2t sin(0.2298730050954942e-t) 其中 a1=157930.3644187159, a2=64.1355812841353, a3=186.854566446932 a4=0.3276998864277856, a5=97857191809355.06。 图2 例3近似解析解Fig.2 The approximate solutions of example 3 实验结果证明,改进的R-L微分变换法可以有效的求解非线性分数阶微分方程,算法不仅构造简单,而且易于编程,具有高精度和较小的计算量,特别是对于求解复杂的分数阶微分方程。在此基础上可以将改进的R-L微分变换法推广到二维或者是三维,用来求解非线性分数阶偏微分方程。 [1]赵家奎.微分变换及其在电路中的应用[M].武汉:华中理工大学出版社, 1988:9. [2]AYAZ F.On the two-dimensional differential transform method[J].Applied Mathematics & Computation, 2003, 143(2):361-374. [3]LAL R, AHLAWAT N. Axisymmetric vibrations and buckling analysis of functionally graded circular plates via differential transform method [J].European Journal of Mechanics-A Solids, 2015, 52: 85-94. [4]ARIKOGLU A, OZKOL I. Solution of fractional differential equations by using differential transform method [J].Chaos Solitons & Fractals, 2007, 34(5):1473-1481. [5]ABDULKAWI M. Solution of Cauchy type singular integral equations of the first kind by using differential transform method [J]. Applied Mathematical Modelling, 2015, 39(8): 2107-2118. [6]VINEET K, SRIVASTAVA M K, KUMAR A S. Analytical approximations of two and three dimensional time-fractional telegraphic equation by reduced differential transform method [J]. Egyptian Journal of Basic and Applied Sciences, 2014,1(1):60-66. [7]CORPORATION H P. Application of multistep generalized differential transform method for the solutions of the fractional-order chua′s system[J].Discrete Dynamics in Nature & Society, 2012,DOI:10.1155/2012/427393. [8]MATTEO A D, PIRROTTA A. Generalized differential transform method for nonlinear boundary value problem of fractional order [J].Communications in Nonlinear Science and Numerical Simulation, 2015,29(1-3):88-101. [9]ABUTEEN E, MOMANI S, ALAWNEH A. Solving the fractional nonlinear bloch system using the multi-step generalized differential transform method[J]. Computers & Mathematics with Applications, 2014, 68(12): 2124-2132. [10] PODLUBNY I. Fractional differential equations[J]. Academic Press Inc San Diego Ca, 1999, 28(2):2. [11] TRUJILLO J J, RIVERO M, BONILLA B. On a riemann-liouville generalized taylor′s formula [J]. Journal of Mathematical Analysis & Applications, 1999, 231(1):255-265. [12] 叶俊杰, 钱德亮. Riemann-Liouville型分数阶微分方程的微分变换方法[J]. 应用数学与计算数学学报, 2009, 23(2):111-120. (编辑亢小玉) DTM-Adomian-pade for solving nonlinear fractional differential equations LIU Chun-feng, ZHANG Hua (College of Science, North China University of Science and Technology, Tangshan 063000, China) An improved generalized differential transformation method is proposed for solving the approximate analytical solution of nonlinear fractional differential equation in the definition of R-L.The method is a combination with differential transformation, Adomian polynomial, Padé approximation. The method is not only simple and has little calculation, but also has higher accuracy. Finally, numerical example is given to verify the effectiveness of the algorithm, which proposes a new calculating scheme for nonlinear fractional differential equations. differential transformation method; nonlinear fractional differential equations; Adomian polynomial; Padé approximant 2015-07-03 国家自然基金资助项目(61170317);河北省自然基金资助项目(A2013209295) 刘春凤,女,河南洛阳人,博士,教授,从事数值计算及其应用研究。 张滑,女,河北唐山人,从事数值计算及其应用研究。 O175.2 A 10.16152/j.cnki.xdxbzr.2016-03-005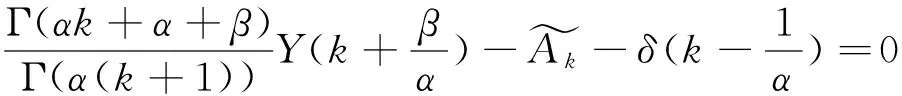
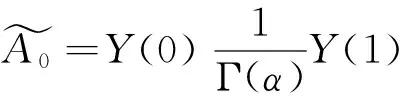
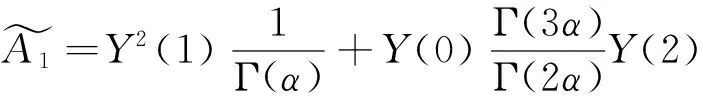
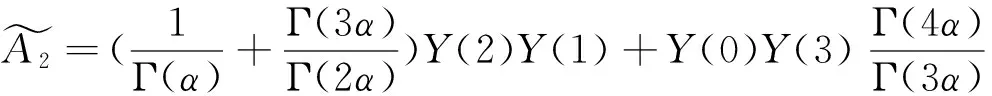
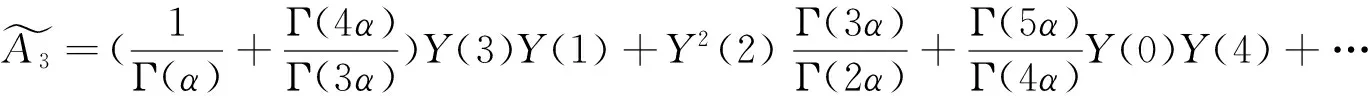
4 结 论
