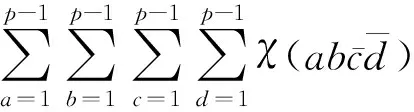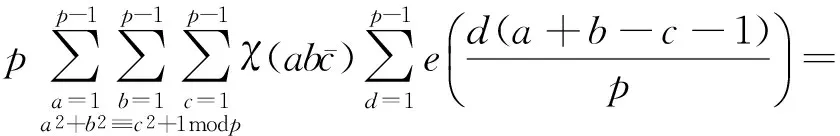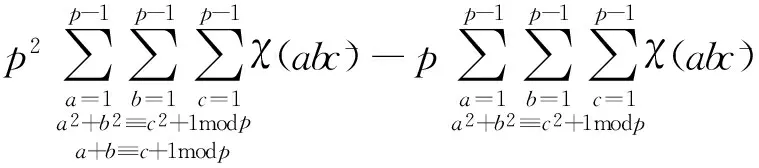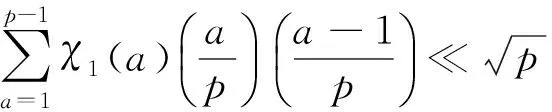关于一类特殊二次高斯和的四次均值
2016-09-29任刚练
任刚练
(咸阳师范学院 数学与信息科学学院, 陕西 咸阳 712000)
【数理科学·数论专栏研究】
关于一类特殊二次高斯和的四次均值
任刚练
(咸阳师范学院 数学与信息科学学院, 陕西 咸阳712000)
该文利用解析方法及三角和的性质,研究了一类特殊二次高斯和的四次均值的计算问题,并得到了一个精确计算公式。
特殊二次高斯和;四次均值; 解析方法;计算公式
设q≥3是一个正整数,对于任意的整数m,经典二次高斯和G(m,χ;q)定义为:
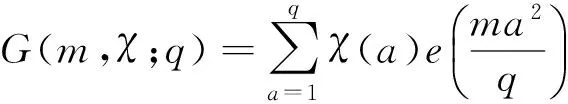
其中,e(y)=e2πiy,χ是模q的Dirichlet特征。
很多学者都对G(m,χ;q)的性质进行过研究,并且得到了一系列重要结果[1-7]。例如,G.I.Perel′muter[5]证明了下面的结论:设p是奇素数,R1(x)和R2(x)是模p的有理函数,χ是模p的任意非主特征,并且满足χ(R1(a))和χ(R2(a))中至少有一个不为常数。那么有估计式
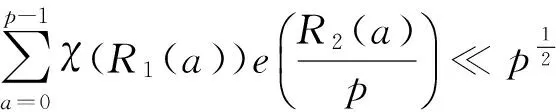
T.Cochrane和郑志勇[2]得到了
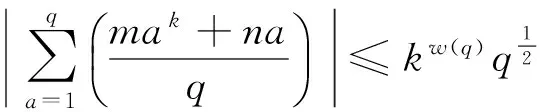
这里,w(q)表示q的所有不同素因子的个数。
张文鹏和韩迪[8]研究了二项指数和的六次均值问题,证明了
对任意的素数p>3且(3,p-1)=1,有
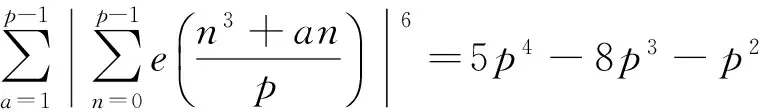
另一方面,如果q=p是奇素数,A.Weil(参阅D.A.Burgess[1])得到了下面的重要结论:
设χ是模p的q阶特征,如果f(x)不是模p的完全q次方,那么有估计
和
(1)
这里,A≪B表示存在某一常数c,使得|A| 当然,式(1)中的估计是最好的。事实上,张文鹏和易媛[6]找到了形如f(x)=(x-r)m(x-s)n的多项式,使得 这里,(r-s,q)=1,m,n和χ满足一些特殊条件。 本文考虑一类特殊二次高斯和的2k次均值 (2) 这里,p是奇素数,k≥2,m和n是整数,且(m,p)=1。 我们考虑式(2)是否存在一个精确的计算公式或渐近公式?对于这一问题,至今似乎没有人研究过,至少现在我们还没有见过相关结论。由于该问题和经典二次高斯和有密切的联系,因此对该问题进行研究是非常有意义的。本文利用解析方法及三角和的性质研究了式(2)的计算问题,并得到了当k=2时式(2)的一个精确计算公式。具体地说,我们证明了下面的结论。 定 理设p是奇素数,那么对模p的任意非主特征χ,m,n为整数,且(m,p)=1,有 对于模p的任意非主特征χ,设误差项E(χ,p)为 p2(2p-3)。 那么,由定理我们可得到下面两个推论。 推论1设p是奇素数,那么对模p的任意非主特征χ,有估计 E(χ,p)=O(p2) 或渐近式 2p3+O(p2)。 推论2设p是奇素数,那么,有恒等式 对任意整数k>2,式(2)是否存在精确的计算公式或渐近公式? 对一般的整数q>2,四次均值 是否存在一个精确的计算公式或渐近公式?这两个问题仍然是没有解决的公开问题,我们今后将继续研究。 这一部分,我们将给出证明定理所需要的几个引理。以下,我们将会用到三角和及模p简化剩余系的性质,这些知识可参阅文献[9],所以这里不再赘述。首先,有 引理1设p是奇素数,χ是模p的任意非主特征,那么有恒等式 证 明因为1≤a≤p-1,有(a,p)=1,若c通过模p的简化剩余系,那么,ca也通过模p的简化剩余系。由此及模p特征的性质,有 (3) 2p-3。 这就证明了引理1。 引理2设p是奇素数,χ是模p的任意非主特征,那么有恒等式 证 明利用证明引理1的方法,模p简化剩余系的性质,有 (p-1)(χ(1)+χ(p-1))+ (4) 如果χ是模p的奇特征(也就是说, χ(-1)=-1),那么,有1+χ(-1)=1-1=0和 因此,由式(4)有 (5) 如果χ是模p的非主偶特征,那么1+χ(-1)=2。因此,由式(4)有 (6) 结合式(5)和式(6),立刻得到恒等式 这就证明了引理2。 引理3[4]设p是奇素数,χ1,χ2,…,χr是模p的Dirichlet特征,且χ1,χ2,…,χr中至少有一个是模p的非主特征,设f(x)∈Fp[X]是次数为d的任意多项式。那么对于成对不同的a1,a2,…,ar∈Fp,有估计 这一节,我们将完成定理的证明。注意到三角恒等式 有 (7) 如果χ(-1)=-1,那么由式(7),引理1和引理2,有 (8) 如果χ(-1)=1,那么由式(7),引理1,2,有 (9) 结合式(8)和式(9),可立刻得恒等式 现在,证明推论1。显然,只需证明估计 (10) 事实上,如果χ(-1)=-1,那么,容易证明 (11) 如果χ是模p的非主特征且χ(-1)=1,那么存在模p的特征χ1,使得χ=χ12。此时,由引理3,有 (12) 结合式(11)和式(12),可立刻推出式(10)。这就证明了推论1。 为了证明推论2,首先,我们注意到 (此公式可参阅文献[10]第7.8节,定理8.2),由式(11),定理和模p特征的正交性,有 -2p2(p-3)-p(p-1)(p-3)+ 这就证明了推论2。 [1]BURGESS D A.On Dirichlet characters of polynomials [J]. Proceeding of the London Mathematical Society, 1963, 13(1): 537-548. [2]COCHRANE T, ZHENG Z. Bounds for certain exponential sums [J]. The Asian Journal of Mathematics, 2000, 4(4): 757-774. [3]GRANVILLE A, SOUNDARARAJAN K. Large character sums: Pretentious characters and the Pólya-Vinogradov theorem [J]. Journal of the American Mathematical Society, 2007, 20(2): 357-384. [4]BOURGAIN J,GARAEV M Z, KONYAGIN S V,et al. On the hidden shifted power problem [J]. SIAM Journal on Computing, 2012, 41(6): 1524-1557. [5]PEREL′MUTER G I. Evalution of a sum containing primes [J]. Soviet Mathematics-Doklady, 1962, 3: 663-667. [6]ZHANG W P, YI Y. On Dirichlet characters of polynomials [J]. Bulletin of the London Mathematical Society, 2002, 34(3): 469-473. [7]WEIL A. On some exponential sums [J]. Proceedings of the National Academy of Sciencs of the United States of America, 1948, 34(5): 204-207. [8]ZHANG W P, HAN D.On the sixth power mean of the two-term exponential sums [J]. Journal of Number Theory, 2014,136: 403-413. [9]APOSTOL T M. Introduction to Analytic Number Theory [M]. New York: Springer-Verlag, 1976. [10] HUA L K. Introduction to number theory [M]. Beijing: Science Press, 1979. (编辑亢小玉) On the fourth power mean of one kind special quadratic Gauss sums REN Gang-lian (College of Mathematics and Information Science, Xianyang Normal University, Xianyang 712000, China) The main purpose of this paper is using the analytic methods and the properties of trigonometric sums to study the computational problem of the fourth power mean of one kind special quadratic Gauss sums, and giving an exact computational formula for it. special quadratic Gauss sums; fourth power mean; analytic method; computational formula 2016-03-11 国家自然科学基金资助项目(11371291);陕西省教育厅科研专项基金资助项目(15JK1794);咸阳师范学院科研专项基金资助项目(09XSYK104) 任刚练,男,陕西乾县人,咸阳师范学院副教授,博士,从事基础数学的教学与研究。 O156.4 A 10.16152/j.cnki.xdxbzr.2016-03-003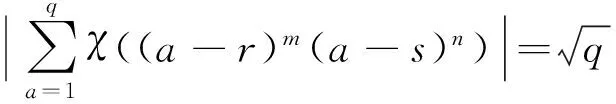

1 若干引理
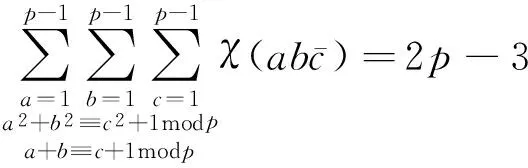
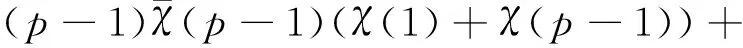
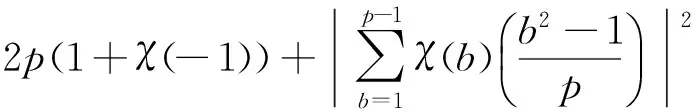
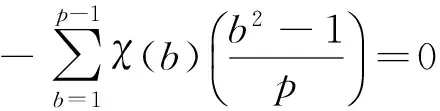
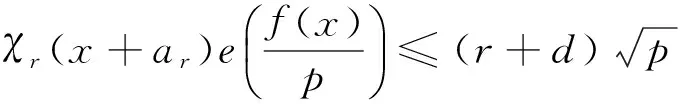
2 定理的证明