关于模p的一类同余方程解的个数

张文鹏

(西北大学 数学学院, 陕西 西安　710127)



【数理科学·数论专栏研究】

关于模p的一类同余方程解的个数

张文鹏

(西北大学 数学学院, 陕西 西安710127)

设p是一个奇素数且满足3|(p-1)。对任意整数k1及k2且满足(k1k2,p)=1,设N(k1,k2;p)表示同余方程k1x3+k2y3≡1modp的解的个数,其中0≤x,y≤p-1。该文的主要目的是利用解析方法,高斯和的性质以及S.Chowla,J.Cowles和M.Cowles等人的重要工作研究N(k1,k2;p)的计算问题,并给出它的一个精确的计算公式,同时提出几个未解决的问题。

素数;三次同余方程;整数解的个数;计算公式;解析方法;高斯和

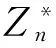
本文的主要目的也是考虑一个类似的堆垒数论问题:设p是一个奇素数且3|(p-1)。对任意整数k1及k2且(k1k2,p)=1，设N(k1,k2;p)表示同余方程

k1x3+k2y3≡1modp

在模p的完全剩余系中的解的个数,即0≤x,y≤p-1。那么人们自然会问,是否存在N(k1,k2;p)的一个确切的计算公式?

关于这一问题,至今似乎没有人直接研究,至少我们没有在现有的文献中看到这样的问题。当然,这一问题是有意义的,至少可以反映出三次剩余的深刻性质。

为叙述方便,我们先给出模p三次剩余的定义。设a是与p互素的整数,如果同余方程x3≡amodp有解,则称a为模p的三次剩余;否则称a为模p的三次非剩余。本文利用三次剩余的概念,解析方法以及S.Chowla等人的深刻结果研究了N(k1,k2;p)的计算问题,并给出了一个简单的计算公式。具体地说也就是证明了下面的定理。

定理1设p为奇素数且满足3|(p-1),那么对任意整数k1及k2且(k1k2,p)=1，有

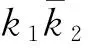
N(k1,k2;p)=p+d-2;

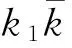
N(k1,k2;p)=p+1+d;

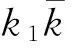
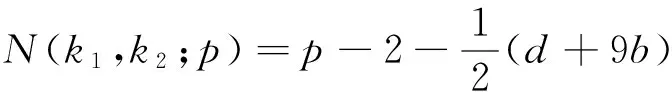
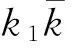
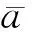
几点注释关于本文中所讨论的问题,这里想说明4点:

1)在本文中只考虑素数p满足3|(p-1)的情况,对于素数p满足(3,p-1)=1的情况而言,由于当x通过模p的一个完全剩余系时,x3也通过模p的一个完全剩余系,所以我们的问题转化为同余方程k1x+k2y≡1modp的解,此时显然有N(k1,k2;p)=p。

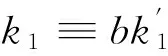
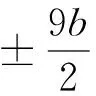
4)我们的另一个公开问题是:对于奇素数p且5|(p-1),设k1和k2是满足(k1k2,p)=1的整数。那么是否存在同余方程k1x5+k2y5≡1modp(0≤x,y≤p-1)解的个数的一个精确的计算公式?此外,把我们考虑的所有问题中的变量换成模p的原根,情况又会怎样?这些都是值得考虑的研究问题。

1　几个简单引理

这节我们给出几个简单引理。其中用到初等数论及解析数论中的一些知识如高斯和的性质等,可以在文献[8-9]中找到,这里不再重复。首先有下面的引理。

引理1设p为奇素数且满足3|(p-1)。那么对任意整数b且(b,p)=1以及模p的任意三阶特征ψ,有恒等式

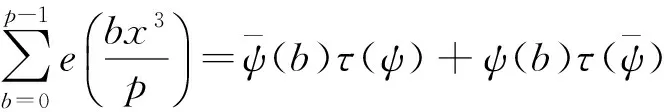
其中τ(ψ)表示高斯和，定义为

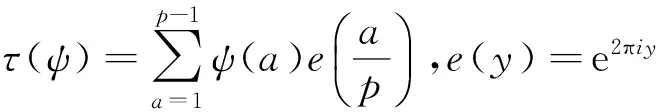
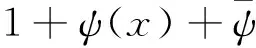
(1)

有

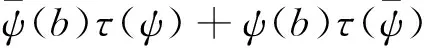
于是就证明了引理1。

引理2设p为奇素数且满足3|(p-1),Ms表示方程

在有限域GF(p)中的解的个数。那么有

M3=p2+(p-1)d。

其中d是由4p=d2+27b2且d≡1mod3唯一确定的。

证 明参阅文献[10]中定理3。

引理3设p为奇素数且满足3|(p-1)。那么对模p的任意三阶特征ψ，有恒等式

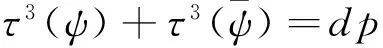
其中d的定义见引理2。

p2+(p-1)d=

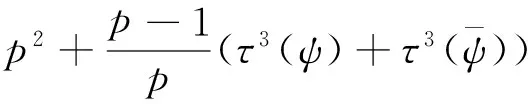
简化后即就是恒等式

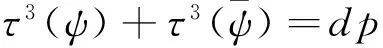
于是证明了引理3。

2　定理的证明

这节我们来完成定理1的证明。事实上应用三角和恒等式(1)、引理1以及高斯和的定义及性质，有恒等式

N(k1,k2;p)=

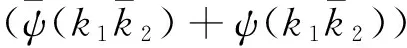
(2)

下面将式(2)中的情况分3种形式讨论:

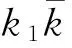
p+d-2。

(3)

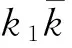
(4)

其中Re(z)表示复数z的实部。由此立刻推出

(5)

(6)

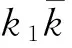
(7)

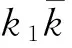
N(k1,k2;p)=p+1+d。

(8)

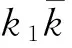
(9)

结合式(3),(6),(7),(8),(9)，并注意到相同表示式的合并，我们立刻完成定理的证明。

[1]SANDER J M. On the addition of units and nonunit modm[J].Journal of Number Theory, 2009，129：2260-2266.

[2]YANG Q H, TANG M.On the addition of squares of units and nonunits modulon[J].Journal of Number Theory,2015，155：1-12.

[3]GOLOMB S.On the algebraic construction for Constas arrays[J].Journal of Combinatoial Theory (Ser. A.), 1984，37：13-21.

[4]WANG Ju-ping. On Golomb′s conjecture[J].Science in China (Ser. A.), 1987，9：927-935.

[5]COHEN S D, ZHANG Wen-peng.Sums of two exact powers[J].Finite Fiels and Their Applications, 2002，8：471-477.

[6]COHEN S D, MULLEN G L.Primitive elements in Costas arrays[J].Applicalde Algebra in Engineering Communication and Computing, 1991，2：45-53; (Corrections)，1992，2：297-299.

[7]ZHANG Wen-peng.On the problem related to Golomb′s conjecture[J].Journal of Systems Science and Complexity, 2003，16：13-18.

[8]APOSTOL T M. Introduction to Analytic Number Theory[M].New York:Springer-Verlag, 1976.

[9]张文鹏, 李海龙.初等数论[M].西安：陕西师范大学出版社, 2008.

[10] CHOWLA S, COWLES J, COWLES M.On the number of zeros of diagonal cubic forms[J].Journal of Number Theory, 1977，9：502-506.

(编辑亢小玉)

On the number of the solutions of one kind congruence equation modp

ZHANG Wen-peng

(School of Mathematics, Northwest University, Xi′an 710127， China)

Letpbe an odd prime with 3|(p-1). For any integersk1andk2with (k1k2,p)=1, letN(k1,k2;p) denotes the number of the solutions of the congruence equationk1x3+k2y3≡1modpwith 0≤x,y≤p-1. The main purpose of this paper is using the analytic method, the properties of Gauss sums and S. Chowla and others′ important work to study the computational problem ofN(k1,k2;p), and giving an exact calculating formula for it. At the same time, several open problems are also proposed.

Prime; cubic congruence equation; the number of the solutions; computational formula; analytic method; Gauss sums

2016-03-11

国家自然科学基金资助项目(11371291)

O156.7

A

10.16152/j.cnki.xdxbzr.2016-03-001

张文鹏，男，1958年8月出生于陕西礼泉。主要从事基础数学的教学与研究，发表学术论文300余篇，其中被SCI检索200余篇；出版教材及专著4部；独立获得陕西省科技进步二等奖及三等奖各一次；独立获得教育部科技进步二等奖一次；作为第一完成人获得陕西省科技进步二等奖二次；获得霍英东教育基金会第四届全国高校优秀教师研究类奖二等奖一次；主持国家自然科学基金项目6次；主持国家教委第四次重点跟踪支持人员基金项目一次；主持陕西省自然科学基金项目4次；教育部博士点基金项目1次；香港王宽诚教育基金项目1次，主持国家基金委国际交流与合作项目1次；曾担任陕西省数学会副理事长、美国Scientia Magna杂志主编；1993年享受政府特殊津贴；1995年被评为首届陕西省科技新星；1997年被评为西省有突出贡献的中青年专家、陕西省优秀留学回国人员；同年入选国家人事部“百千万人才”及陕西省“三五人才”第一层；2000年被评为陕西省有突出贡献专家。

【主持人语】数论是数学中最古老而又年轻的学科，这一看起来似乎矛盾的说法并不奇怪，因为这是从数论的两个不同角度来说明这一独特的数学学科！一方面说它最古老是因为自从有了人类的文明，就有了数论内容, 也就是当时的自然数，所以说它是最古老的数学分支；其次，我们说数论是一门年轻的数学学科，这是因为数论中未解决的问题非常多， 从一开始学习初等数论课程起，每一节课都可能遇到不少数论难题，我们大家所熟知的哥德巴赫猜想、孪生素数问题等也只是众多未解决的数论难题中的几个特例！ 事实上许多古老的数论难题至今没有解决，同时又出现了一大批新的数论难题，而且新问题的出现往往要比老问题解决的速度快得多，这样就使得未解决的数论难题越来越多，因而显得这一学科很不成熟，很年轻！

本次数论专辑栏目主要针对数论中的一些经典问题进行了研究， 其中包括特殊同余方程解数个数的计算问题、奇完全数的素因数指标问题、二次高斯和的四次均值公式以及著名数列倒数积的恒等式等四个内容，这些问题虽然不是数论中的著名难题，但是它们也具有代表性，特别是在“关于模p的一类同余方程解的个数”一文中，作者提出了许多有待于读者进一步研究的新问题，这些内容无疑对有关内容的进一步研究将起到十分积极的促进作用！

主持人：张文鹏，西北大学数学学院二级教授，博士生导师。