关于辐角改变量算法的两点注记

储亚伟，王　雪，黄　瑞

（阜阳师范学院 数学与统计学院，安徽 阜阳 236037）

关于辐角改变量算法的两点注记

储亚伟，王雪，黄瑞

（阜阳师范学院 数学与统计学院，安徽 阜阳 236037）

确定多值函数的单值分支是复分析的教学难点之一，辐角改变量法是解决单值分支问题的主要方法。对于含有z-a的函数的辐角改变量，现行教材多采用平移坐标原点的“间接辐角改变量法”计算；对于含有a-z的函数的辐角改变量，则借助公式ΔCarg（a-z）=ΔCarg（z-a）转成“间接辐角改变量法”计算。文章通过构造反例表明，上述算法及公式均存在误区，即在考虑到割线的因素时，上述方法与公式未必成立。同时，分析了“直接辐角改变量法”与“间接辐角改变量法”的本质区别，得到“间接辐角改变量法”及上述公式成立的条件。作为应用，给出不能使用“间接辐角改变量法”计算单值分支的实例。上述注记与实例将有效地克服相关的教学难点。

单值分支；辐角改变量；割线；反例；注记；教学

极限是分析数学的基本工具之一，唯一性是极限的重要特征。因此，凡涉及到函数的分析性质（如连续性、可导性或解析性、可积性等），都要求研究的函数是单值的。在复分析中，由于指数函数具有周期性，导致初等多值函数中的对数函数、根式函数及反三角函数均是多值的。而复分析研究的主要对象是解析函数，因此，多值函数的单值化问题是复分析的重要课题之一［1］。辐角改变量法是解决单值分支问题的主要方法，即把支点确定、可单值分支区域的判定和单值分支的表达式或单值分支求值的计算都归结为辐角改变量的计算［1-3］，由此可见辐角改变量正确算法的重要性。

对于表达式中含有z-a或a-z的函数，在可单值分支区域内，其辐角改变量的常用算法是借助公式ΔCarg（a-z）=ΔCarg（z-a），使用平移原点的“间接辐角改变量法”（定义1）。该方法是研究多值函数单值分支理论的重要方法，在单值区域的判定和单值分支的计算中起到关键作用［4-12］，是求解或判定多值函数可单值分支区域的有效方法。然而，在单值分支的计算问题上，上述公式及算法却存在误区。本文通过构造反例指出，在考虑到割线的因素时，上述公式与方法未必成立，同时，指出其成立的条件。作为应用，给出不能使用上述公式与方法计算单值分支的实例。

1　预备知识

定义1［2］设C是复平面内不通过点a的一条简单曲线，z0是C的起点，z1是C的终点。当动点z从z0沿C不穿过割线连续变动到z1时，向量所旋转的角称为arg（z-a）在C上的间接改变量，简称辐角改变量，记为ΔCarg（z-a）。

使用定义1求ΔCarg（z-a），相当于把坐标原点平移到了a点，求向量所旋转的角，我们称这种平移原点的算法为“间接辐角改变量法”。与此对应，我们有下面的“直接辐角改变量法”：

定义2设C是复平面内不通过点a的一条简单曲线，z0是C的起点，z1是C的终点。当动点从z0沿C不穿过割线连续变动到z1时，相应地，动点z从z′1=z0-a不穿过割线连续变动到z′1=z1-a，此时向量所旋转的角称为arg（z-a）在C上的直接改变量，简称辐角改变量，记为ΔCdarg（z-a）。类似地，可定义arg（a-z）在C上的直接改变量ΔCdarg（a-z）。

显然，“直接辐角改变量法”需要先把C的起点与终点代入函数，再以向量′按动点z′不穿过割线且尽可能与C保持一致的方向所旋转的角来计算辐角改变量。当a=0时，定义1与定义2的计算结果相等。一般情况下，在确定支点和判定可单值分支区域的研究过程中，由于不受割线的影响，上述两种算法得到的辐角改变量完全一致［1-3］，且有

引理1［1］

然而，在多值函数的另一个重要问题——单值分支的计算中，因受割线的影响，间接辐角改变量法与公式（1）的使用需要当心。本文以根式函数为例，通过对比“间接辐角改变量法”和“直接辐角改变量法”等方法后指出：在单值分支的计算问题中，使用定义1与定义2得到的辐角改变量可能不同，且公式（1）也未必成立。为了叙述方便，我们还需要下面的公式。

引理2［1-3］设D为（其中P（z）为z的有理分式，n≥2为整数）的可单值分支区域，f（z）在z0∈D的初值为 f（z0）的单值分支在z1∈D的终值f（z1）为

其中C为D内以z0为起点、z1为终点不穿过割线的约当曲线。

2“间接辐角改变量法”的使用误区

“间接辐角改变量法”的使用误区——默认与“直接辐角改变量法”的结果相同。

例1在复平面内，取割线

解因 f（z）的支点是0，1，∞，在G内 f（z）能分出三个单值解析分支。

解法一（间接辐角改变量法）当z从z0=3沿G内一条简单曲线C不穿过割线连续变动到z1=i时，由图1易得

于是

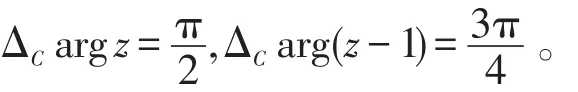
再由题设，可设arg f（3）=0（允许相差2π的整数倍）。由公式（2）知，

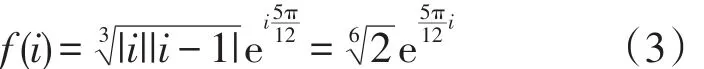
图1　例1的示意图

解法二（直接辐角改变量法）当z从z0=3沿G内简单曲线C连续变动到z1=i时，z′=z-1不穿过割线从始点z′0=2连续变化到终点z′1=i-1的路径如C1，由图1易得

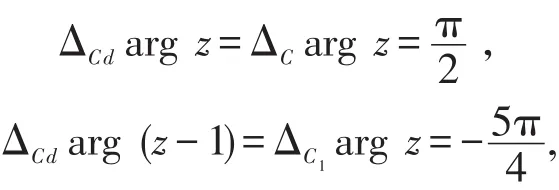
于是

再由题设，可设arg f（3）=0（允许相差2π的整数倍）。由公式（2）知，

对于例1，使用上述两种方法却得到完全不同的答案！事实上，当单值区域确定后，给定的分支便是单值函数，它在定点处的值不可能出现两个不同答案。上述两个结果到底孰是孰非？由公式（2）可知，单值分支的辐角改变量

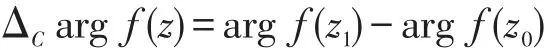
应该是把起点z0与终点z1代入函数表达式后的辐角改变量（动点不穿过割线），而间接辐角改变量法是把坐标原点平移到a点后，计算当动点z从z0沿C不穿过割线连续变动到z1时向量所旋转的角，此过程可能会忽略割线对函数初值 f（z0）与终值 f（z1）的影响。如在本例中，当动点从3沿C不穿过割线变化到i时，“间接辐角改变量法”求得，而代入后对应的动点从2逆时针绕变到i-1时必穿过割线，此时动点不穿过割线从2变动到i-1的直接辐角改变量为

我们也可以换种方法求解：

由

与（4）相同。

即间接辐角改变量法与直接辐角改变量法的计算结果不相等。根据公式（2）或解法三，此时应该用直接辐角改变量法计算。

注1由上例分析可知，间接辐角改变量法的使用条件为：

即当动点沿C不穿过割线从z0连续变动到z1时，向量所旋转的角与相应的动点从z′0=z0-a不穿过割线连续变动到z′1=z1-a时向量所旋转的角相同，则两种算法的结果一致，否则，应采用直接辐角改变量法计算arg（z-a）的改变量。

注2间接辐角改变量法的优点在于简洁方便，但却可能因忽略割线因素而出错；直接辐角改变量法需要代入计算，但结果准确、直观具体、适用范围更广。

3　计算ΔCarg（a-z）的误区

计算ΔCarg（a-z）的误区——用ΔCarg（z-a）代替ΔCarg（a-z）。在确定支点和求可单值分支区域时，由于不受割线的影响，可以用ΔCarg（z-a）代替ΔCarg（a-z）来计算辐角改变量。但在单值分支的计算过程中，可能出现受割线位置的影响而导致二者不相等的情况（为简单起见，取a=0）：

图2　例2的示意图

解法一（间接辐角改变量法）当z从z0=1-i不穿过割线沿G内简单曲线C变动到z1=1+i时，量所旋转的角为 ΔCarg z。由图 2知，于是

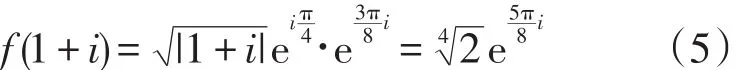
注3解法一用ΔCarg z代替了ΔCarg（-z）。然而对于例2，使用间接辐角改变量法，当z从z0=1-i不穿过割线沿C变动到 z1=1+i时，对而言，向量从转到，转角为整数倍）。由公式（2）知，对于ΔCarg（-z）而言，该转角相当于对应向量逆时针转到，但此时动点从E变动到F时必穿过割线，不符合要求。因此，此时不穿过割线的路径应该沿C1（参图2路径），从而用间接辐角改变量法求得

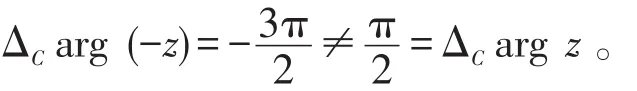
解法二（直接辐角改变量法）当z从z0=1-i 沿G内不穿过割线的简单曲线连续变动到z1=1+i时，由图2易得

于是

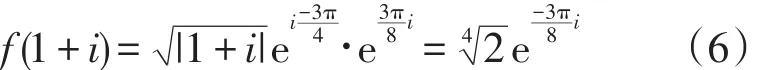
解法三（限定辐角法）由于沿着原点从负实轴割开，因此可限定arg z∈（-π，π）（允许相差2π的整数倍）。于是当z0=1-i时，。由

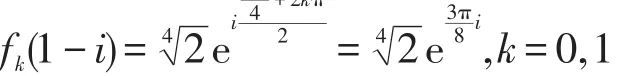
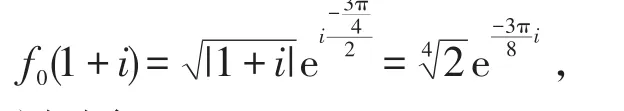
与（6）相同。

注3结合第二部分的分析可知，在计算ΔCarg（a-z）时 ，使 用ΔCarg（z-a）代 替ΔCarg（a-z）（即使用引理1）的条件是

ΔCarg（a-z）=ΔCarg（z-a）=ΔCdarg（a-z），否则，即使ΔCarg（a-z）=ΔCarg（z-a），也不能使用公式（1）或间接辐角改变量法和，例3便是一反例。

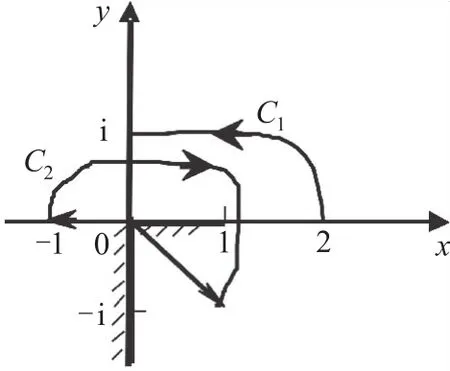
图3　例3的示意图

解采用直接辐角改变量法，如图3，当定点从z0=2沿G内一条不穿过割线的简单曲线C1变动到z1=i时，

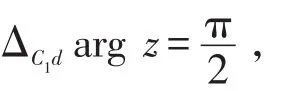
而分量函数1-z的辐角改变量等于定点z′1=-1 沿G内不穿过割线的简单曲线C2变动到z′2=1-i时（见图3）向量所旋转的角，即

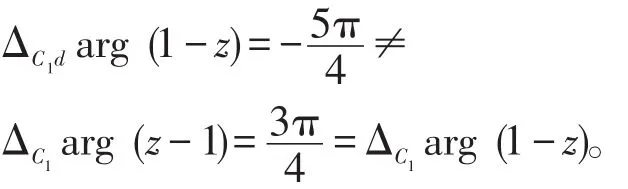
从而

再由题设，可设arg f（2）=π（允许相差2π的整数倍）。由公式（2）知，

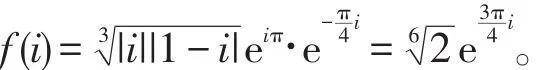
注4本例在许多文献中均有讨论［3-12］。由于沿原点从负虚轴割开，再根据本题起点、终点的分布情况，可限定允许相差2π的整数倍），使用“限定辐角法”也能得到上述结论。若使用“间接辐角改变量法”，用

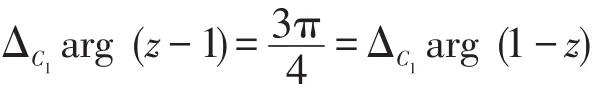
［1］ 刘士强，林玉波.关于初等多值函数单值分支问题［M］.北京：兰州大学出版社，1993：4，18，50-56.

［2］ 路见可，钟寿国，刘士强.复变函数［M］.2版.武汉：武汉大学出版社，2007：39-43.

［3］ 钟玉泉.复变函数论［M］.4版.北京：高等教育出版社，2013：65-84.

［4］ 李志广，石磊.一类多值函数的单值化方法［J］.山西大同大学学报（自然科学版），2009，25（6）：13-16，20.

［5］ 王凡彬.一类多值解析函数的计算问题［J］.嘉应学院学报（自然科学版），2009，27（6）：5-8.

［6］ 王凡彬.关于一类复多值函数的计算问题［J］.内江师范学院学报，2006，21（2）：10-12.

［7］ 朱顺东.关于求根式函数单值解析分支上辐角的一点注记［J］.安徽师范大学学报（自然科学版），2006，29 （4）：329-331.

［8］ 魏立明.对一个教学难点的研究［J］.贺州学院学报，2008，24（3）：106-108.

［9］ 张萍萍.根式函数的函数值计算［J］.滨州学院学报，2009，25（6）：64-67.

［10］张忠诚，柳翠华.确定多值函数单值解析分支值的一种简易方法［J］.长春师范学院学报（自然科学版），2010，29（5）：3-5.

［11］黄志刚，孙桂荣.从一道多值解析函数题的解法谈起［J］.河西学院学报，2011，27（2）：26-29.

［12］冯志新.复数域中两类函数的单值分支问题［J］.衡水学院学报，2012，14（1）：29-32.

Two notes on the methods to calculate the argument increment

CHU Ya-wei，WANG Xue，HUANG Rui

（School of Mathematics and Statistics，Fuyang Normal University，Fuyang Anhui 236037，China）

How to determine a single-valued branch of multi-valued functions，which is a teaching difficult point in complex analysis，can be solved by the method to calculate the argument increment.When the expression of a multi-valued function has the factorz-a，the argument increment ofarg（z-a）can be derived in the present textbooks by the indirect method of translation of origin of coordinates.When the expression of a multi-valued function has the factorz-a，the argument increment of arg（z-a）can be derived by the indirect method of calculation of argument increment by means of the formula ΔCarg（a-z）=ΔCarg（z-a）.By counterexamples，it is illustrated in this paper that there are still misunderstandings in the indirect method and the above formula for the calculation of a single-valued branch，namely，they may not be right when one considers the branch line factor.Meanwhile we analyze the essential difference of both indirect method and direct method for the calculation of argument increment，and establish two important conditions which make the indirect method and above formula hold. As an application，an example in which the indirect method does not hold is given.These notes and examples will overcome the difficulty in teaching effectively.

single-valued branch；argument increment；secant line；counterexample；note；teaching

O174.5

A

1004-4329（2016）03-102-05

10.14096/j.cnki.cn34-1069/n/1004-4329（2016）03-102-05

2016-05-08

国家自然科学基金（11371330）；安徽省教育厅自然科学基金（KJ2014A196）；安徽省质量工程项目（2013jyxm553，2014zy138）资助。

储亚伟（1977-），男，博士，副教授，研究方向：几何分析。