一题多变探究三角最值

◇　江苏　苗　壮



一题多变探究三角最值

◇江苏苗壮

解三角形中的最值问题,归纳起来主要有求边的最值、角的最值、面积的最值．这些问题的求解通常有2种策略: 1)结合余弦定理,利用均值不等式求最值; 2)利用正弦定理,将其转化为三角函数最值问题．

(1) 求角B;

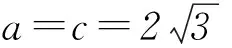
1　求面积的最值

(1) 求角B的值;

(2) 如果b=2,求△ABC面积的最大值.

2　求角的最值

(1) 证明:a+b=2c;

(2) 求cosC的最小值.

化简得

2(sinAcosB+sinBcosA)=sinA+sinB,

即

2sin(A+B)=sinA+sinB．

因为A+B+C=π,所以sin(A+B)=sinC,从而sinA+sinB=2sinC．由正弦定理得a+b=2c.

当且仅当a=b时,等号成立.故cosC的最小值为1/2.

3　求边的最值

(1) 求角B;

图1

(2) 如图1,将△ABC置于圆O中,当点B在优弧AC上运动时,B的大小不变,AB过圆心O时,AB取得最大值,即c最大．

4　求两边之和的最值

(1) 求c的值;

(2) 求a+b的取值范围.

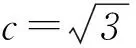
图2

总之,求解与解三角形有关的最值问题,我们只要把握处理问题的基本策略,就能以不变应万变,实现问题的顺利解决．

江苏省灌南高级中学)