三角函数中最值问题解法探究
2016-09-28云南
高中数理化 2016年17期
◇ 云南 闵 敏 韦 欢
北京 童嘉森2(特级教师)
三角函数中最值问题解法探究
◇云南闵敏1韦欢1
北京童嘉森2(特级教师)
三角函数最值问题是三角函数中的基本内容,也是难点之一,对三角函数恒等变换、综合应用能力要求较高.该内容重点考查学生转化与化归、函数与方程、数形结合等数学思想的应用,有一定的灵活性,要求学生具备一定的分析问题、解决问题、运算求解的能力,突破此内容要靠平时多积累.笔者归纳了求三角函数值域的3种方法与读者分享.
1 用三角方法求三角函数的最值


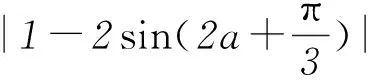






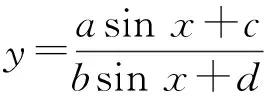
2 用代数方法求三角函数的最值


y=1-sin2x+2asinx=
-(sinx-a)2+a2+1.
若a>1,则当sinx=1时,
ymax=-(1-a)2+a2+1=2a.
若-1≤a≤1,则当sinx=a时,
ymax=-(a-a)2+a2+1=a2+1.
若a<-1,则当sinx=-1时,
ymax=-(-1-a)2+a2+1=-2a.
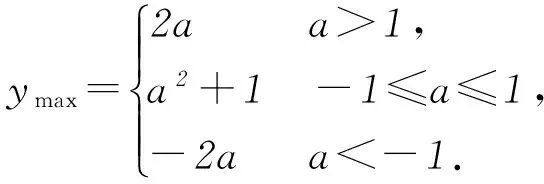



所以

故
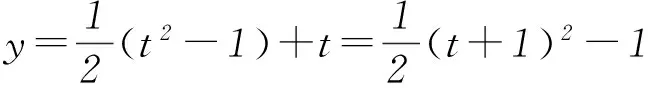
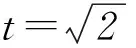
方法2y=sinx·cosx+sinx+cosx=


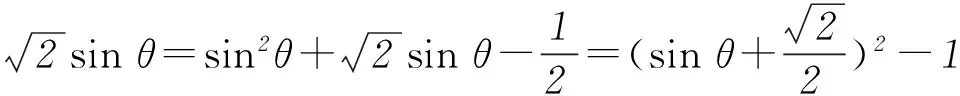
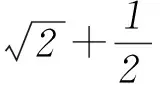


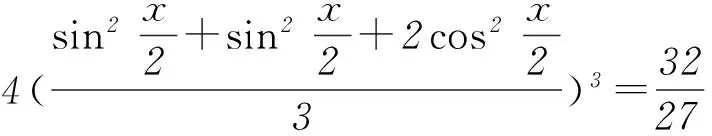

方法2y=cos3x+sin2x-cosx=cos3x+1-cos2x-cosx.
令cosx=t(-1≤t≤1),则
y=t3-t2-t+1(-1≤t≤1),
y′=3t2-2t-1=(t-1)(3t+1),


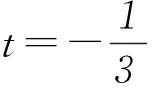

1) y=asin2x+bsinx+c
或
y=acos2x+bcosx+c(a≠0),
可通过令t=sinx或t=cosx转化为关于t的二次函数在区间[-1,1]上的最值.
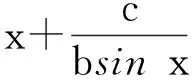
3)y=a(sinx±cosx)+bsinx·cosx.


把三角问题转化为代数问题解决.
以上3种形式可统称为换元法,换元后一定要注意“新元”的取值范围.
3 用解析法求三角函数的最值



图1






2sinx+(3-y)cosx=4-2y.
设 a=(2,3-y),b=(sinx,cosx).
由柯西不等式的向量形式|a·b|≤|a||b|得