圆周运动问题备考的“1、2、2、3”
2016-09-28山东
◇ 山东 孙 飞
圆周运动问题备考的“1、2、2、3”
◇山东孙飞
1 构建1个知识网络——解题的知识依托

2 内化2种模型——化繁为简的有效途径
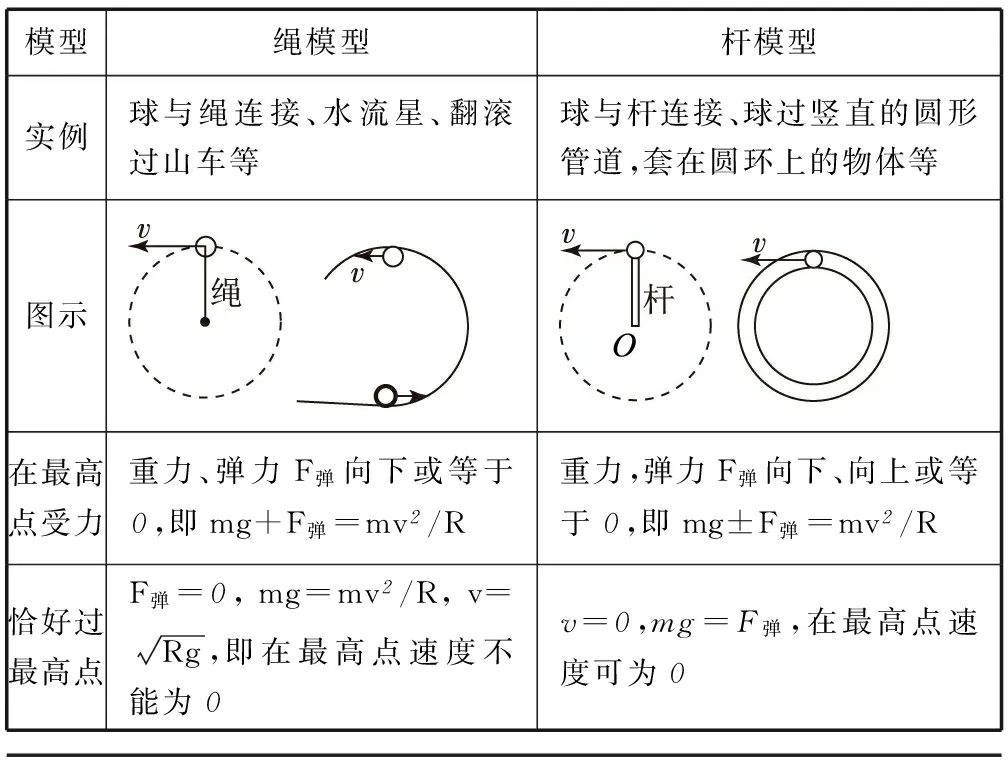
模型绳模型杆模型实例球与绳连接、水流星、翻滚过山车等球与杆连接、球过竖直的圆形管道,套在圆环上的物体等图示在最高点受力重力、弹力F弹向下或等于0,即mg+F弹=mv2/R重力,弹力F弹向下、向上或等于0,即mg±F弹=mv2/R恰好过最高点F弹=0,mg=mv2/R,v=Rg,即在最高点速度不能为0v=0,mg=F弹,在最高点速度可为0
3 铭记2个特点——这是快速解题的切入点
1) 向心力一定指向圆心,而只有做匀速圆周运动的物体的合力才始终指向圆心.

图1

A小球A的合力小于小球B的合力;
B小球A与框架间可能没有摩擦力;
C小球B与框架间可能没有摩擦力;
D圆形框架以更大的角速度转动,小球B受到的摩擦力一定增大

由于合力提供向心力,依据向心力表达式F=mrω2,已知2球质量、运动半径和角速度都相同,可知向心力相同,即合力相同,故选项A错误.小球A受到重力和弹力的合力不可能垂直指向OO′轴,故一定存在摩擦力,而B球的重力和弹力的合力可能垂直指向OO′轴,故B球摩擦力可能为0,故选项B错误,选项C正确.由于不知道B是否受到摩擦力,故而无法判定圆形框架以更大的角速度转动时,小球B受到的摩擦力的变化情况,故选项D错误.
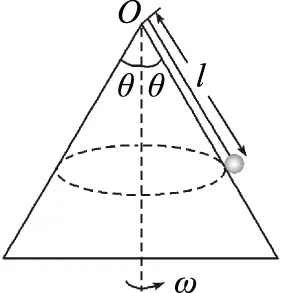
图2

(1) 若要小球离开锥面,则小球的角速度ω0至少为多大?
(2) 若细线与竖直方向的夹角为60°,则小球的角速度ω′为多大?

FTcosθ=mg,FTsinθ=mω2·lsinθ.
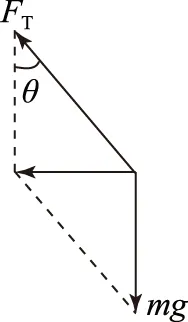
图3
(1)若要小球刚好离开锥面,则小球受到重力和细线拉力如图3所示.小球做匀速圆周运动的轨迹圆在水平面上,故向心力水平.

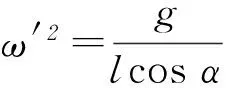


图4

A小球的质量为aR/b;
B当地的重力加速度大小为R/b;
Cv2=c时,在最高点杆对小球弹力方向向上;
D若v2=2b,则在最高点杆对小球弹力大小为2a

4 突破3个题型
4.1圆周运动的临界极值问题

(1) 若装置匀速转动的角速度为ω1时,细线AB上的张力为0,而细线AC与竖直方向的夹角仍为37°,求角速度ω1的大小;
(2) 若装置匀速转动的角速度为ω2时,细线AB刚好竖直,且张力为0,求此时角速度ω2的大小;
(3) 装置可以以不同的角速度匀速转动,试通过计算,在图6的坐标中画出细线AC上张力FT随角速度的平方ω2变化的关系图象.

图5 图6





FTcosθ=mg,FT=mg/cosθ=12.5 N.
ω1≤ω≤ω2时细线AB松弛, 细线AC上张力的水平分量等于小球做圆周运动需要的向心力
FTsinα=mω2lsinα,FT=mω2l.ω>ω2时,细线AB在竖直方向绷直,仍然由细线AC上张力的水平分量提供小球做圆周运动需要的向心力,则
FTsinθ′=mω2lsinθ′,
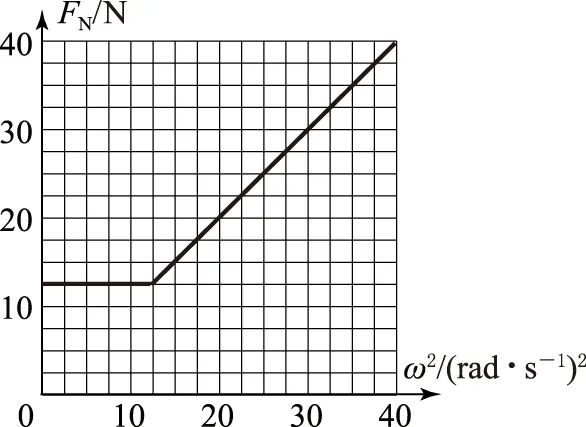
图7
即
FT=mω2l.

4.2圆周运动中的连接体问题

图8



4.3圆周运动的多过程问题


图9
A2钉子间的距离为绳长的1/6;
Bt=10.5 s时细绳拉力的大小为6 N;
Ct=14 s时细绳拉力的大小为10 N;
D细绳第3次碰钉子到第4次碰钉子的时间间隔为3 s

山东省枣庄市台儿庄区职业中专)
