数控机床误差原因和精度补偿
2016-09-27程卫锋
程卫锋
(上海西重所重型机械成套有限公司,上海,201900)
数控机床误差原因和精度补偿
程卫锋
(上海西重所重型机械成套有限公司,上海,201900)
数控机床产生误差的原因主要有机械变形、磨损、热误差、静态响应误差和动态响应误差等,要提高数控机床的加工精度,必须对上述误差原因进行分析,找到合适的误差补偿方法。本文对数控机床误差原因进行了相关探讨,提出了螺距补偿、温度补偿、摩擦力补偿等改善措施。
数控机床;误差原因;改善措施
机械制造业是国民经济的支柱产业之一,而数控技术是现代制造技术的基础,数控技术的广泛应用使普通机械被数控机械所替代,导致了全球制造业的深刻变革。目前我国虽已成为制造业第一大国,但却面临着“大而不强”的问题,究其原因,高精度的加工装备是一个瓶颈。到2025年我国要迈入制造强国行列,高精度数控机床的研究是一个重要课题,要提高数控机床精度,就必须针对数控机床产生误差的原因进行分析,找到合适的误差补偿方法。
1 数控机床机械变形误差和螺距补偿
数控机床机械变形误差主要是由机床结构变形造成,并且是一个较小的固定误差值,常见于数控机床主轴、测量臂等变形而造成加工的工件超差。以国内某一型号的磨床为例,磨床的砂轮滑架沿Z轴方向运行时,相对X轴方向出现了机械变形误差,见图1。
螺距补偿的原理是采用一次插补法,拟合误差曲线,生成一个误差曲线二维数组,然后对磨削曲线进行补偿,从而消除机械变形误差。设某次用激光校准仪测量磨床误差,得到10个点的数据如下:

若有一点为Xm,X1<Xm<X2,则

根据要求的拟合精度可以选择插补点数,一般一米长度取100-200点,插补后生成的误差曲线二维数组需要跟据数控机床的坐标系统特点确定对磨削曲线的补偿方式。如图1中的误差曲线与X轴正相关,因此需要将误差曲线与磨削曲线相加,如果是测量臂误差曲线与X轴负相关,则需要将误差曲线与磨削曲线相减,补偿后的磨削曲线去CNC。
另外,为了避免误差曲线在拐点处出现较大的跳跃,可以选择不同的插补公式,或采用高阶插补方法,对拐点处作平滑处理,防止数控机床运行中出现电机轴超速或过电流故障。
2 数控机床热误差和温度补偿
热误差是由温度变化对机床轴的运行精度造成的影响,温度变化通常由环境温度变化、刀具发热传导、电机发热传导、传动链运动发热、液压润滑油温的变化等引起,针对不同的温度变化原因可采取不同的改善措施,例如恒温车间、降低传动链阻力、油温恒温控制等,但由于热误差产生的原因多,并一直处在变化状态,因此上述方法很难达到较好消除热误差的效果。

图1 数控机床机械变形误差示意图
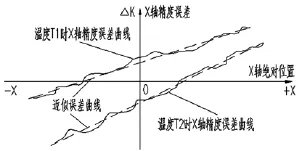
图2 某X轴精度误差曲线

图3 位置关联的近似误差曲线数学分解
温度补偿是找出温度变化与机床轴运行精度误差之间的规律,建立合适的数学模型,然后进行软件补偿的一种方法。经过测量发现,轴在某温度时的误差曲线如图2所示,可以看出,在一定温度时,轴的误差与轴的绝对位置关系基本上是一条斜线,不同温度时,其斜率、零点不同,但都是一条近似的斜线。
轴在不同温度下的误差近似曲线可以用图3中的数学分解来确定一个数学关系式,即

式中:ΔKx为X轴在位置Px时的温度补偿值;
K0(T)为轴在参考点位置时的温度补偿值;
Px为轴的实际绝对位置值;
P0为轴的参考点位置值;
tanβ(T)为误差近似曲线的斜率。
如果能够掌握不同温度下的近似误差曲线的斜率和零位误差的规律,则可以通过在相应轴的适当测量点取得温度值,再根据实验测量值计算出的规律,生成不同温度对应轴的不同位置需要的误差补偿量,即
tempCorrection[T1,ΔK1]…tempCorrection[Tn,ΔKn]
用该误差补偿量对磨削曲线进行处理,补偿后的磨削曲线去CNC,从而以软件补偿来减少温度变化对轴精度误差的影响。
由于对应每一个X轴绝对位置坐标都有一个温度补偿值,因此温度补偿值引起的轴位置修整必须在一个插补循环中完成,不能累积,所以如果温度补偿值过大,会造成插补轴的速度不能满足要求,温度补偿算法会根据主动轴、从动轴、插补周期和补偿值大小来计算允许的温度补偿最大速度附加值,当速度超过上限时,自动对主动轴和从动轴降速处理,以满足误差补偿同时机床能稳定运行。
3 数控机床响应误差和摩擦力补偿
机械轴传动链中的齿轮、丝杆、导轨等都存在摩擦力,轴由静止开始运动时需克服静摩擦力,静摩擦力对轴的动态特性有较大影响,而对于往复运行的轴,在换向时则是摩擦力影响较大的阶段。
圆弧插补时其中一个轴不换向而另一个轴换向,则换向轴的摩擦力对其动态特性的影响,将直接影响到其是否能跟得上圆弧插补的轨迹,所以摩擦力补偿常用于圆弧插补的圆度补偿。
在多数情况下,轴在整个加速运行范围内,摩擦力是一个改变的值,例如,加速度越大,则摩擦力越大,且在克服最初的静态摩擦力开始运动时的摩擦力也会越大,因此,常用的摩擦力补偿方法为根据幅度适应曲线来确定实时补偿值,一般常用的幅度适应摩擦力补偿曲线如图4。
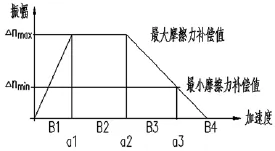
图4 幅度适应摩擦力补偿曲线

图5 圆度测试4种形状
设当前加速度为a,当前补偿幅度值为Δn,则四个曲线段可分别表示为:
(1)曲线段B1(a<a1):Δn=ΔnmaxX(a/a1);
(2)曲线段B2(a1≤<a≤a2):Δn=Δnmax;
(3)曲线段B3(a2<a<a3):Δn=Δnmax-(Δnmax-Δnmin)X(a-a2)/(a3-a2);
(4)曲线段B4(a3≤a):Δn=Δnmin;
要确定该曲线中的各参数,需要经过多次测试,包括在轴整个速度、插补半径范围内作测试,然后根据测试的结果经计算得出最适合的参数值。
另外也可以采用常数值摩擦力补偿方法,结合机床的圆度测试功能来进行补偿测试,具体操作方法是:
(1)机床正常运行,摩擦力补偿不投入;
(2)进行圆度测试,以常规运行参数进行;
(3)设置一个较小的摩擦力补偿幅度值和时间常数,摩擦力补偿投入;
(4)进行圆度测试,与步骤2相同;
(5)根据圆度测试的结果,调整摩擦力补偿幅度值和时间常数,调整方法如下:
圆度测试结果通常有4种形状,见图5。
图形A表示摩擦力补偿幅度值太小;图形B表示摩擦力补偿幅度值太大;图形C表示摩擦力补偿时间常数太小,图形D表示摩擦力补偿时间常数太大。
如果经过常数值摩擦力补偿后,在整个工作速度与半径范围内其插补特性较好,圆度测试满足要求,则摩擦力补偿结束。如果其补偿效果不能达到要求,且摩擦力特性与轴的加速特性有关,则可以采用幅度适应方法进行摩擦力补偿。
4 结语
通过对数控机床误差产生原因和误差补偿方法的分析,针对不同的误差类型,通过理论分析,建立数学模型,从算法和软件编程上提出了误差补偿的方法,使数控机床误差补偿更灵活、高效,且能解决常规方法难以消除的误差,提高了数控机床的加工精度。
(References)
[1]韩振宇,付云忠,等.机床数控技术[M].哈尔滨:哈尔滨工业大学出版社.
[2]陈先锋,何亚飞,朱弘峰,等. SIEMENS数控技术应用工程师[M].人民邮电出版社.
[3]姜彬,赵志刚,孙明陆,等.数控机床主轴热特性分析[J].天津大学学报,2013,46(9):846-850.
