基于滑模控制器的四旋翼飞行器控制

杨兴明,　李文静

(合肥工业大学 计算机与信息学院,安徽 合肥　230009)



基于滑模控制器的四旋翼飞行器控制

杨兴明,李文静

(合肥工业大学 计算机与信息学院,安徽 合肥230009)

文章针对四旋翼飞行器的飞行控制设计了滑模控制器。针对飞行器的高度控制,设计了一种基于滑模控制方法的控制器,并根据李雅普诺夫稳定性理论证明了飞行器系统的所有信号最终是一致有界的;针对飞行器的姿态控制设计了滑模控制器,并对其进行了稳定性证明,且针对该控制器产生较大抖振的问题提出了采用双幂次趋近率的改进方法。仿真结果证明了设计的控制器能较好地控制四旋翼飞行器。

四旋翼飞行器;滑模控制;抖振;双幂次趋近率

0　引　　言

近年来,四旋翼飞行器由于被广泛使用而成为国内外研究热点。飞行器的控制研究包含多个领域,如数字滤波、基于GPS的位置估计及传感器的数据融合等。控制算法的正确与否直接影响控制系统的品质,甚至决定整个系统的成败,因此,各国学者均致力于控制算法的研究。其中由于滑模控制系统的滑动模态对满足匹配条件的参数变化与外部扰动具有完全鲁棒性,因而受到广泛重视。文献[1]针对飞行器的控制设计了滑模控制器;文献[2]基于滑模控制方法设计了实时高度鲁棒控制器;文献[3]利用滑模变结构控制理论设计出一种基于误差四元数的滑模变结构控制飞行器姿态跟踪控制律;文献[4]提出了滑模容错控制方法。

滑模控制方法[5]能够实现系统解耦控制且实现简单,并对匹配不确定性和未建模动态具有不变性,因此近几十年来得到了广泛深入的研究,但是传统滑模控制方法抖振严重,现阶段解决此问题的主要手段有高阶滑模控制和非奇异终端滑模控制等。滑模控制系统具有其优越鲁棒性的前提是系统状态运动在滑动模态上,而在趋近阶段滑模控制系统仍对参数不确定性和外界干扰敏感,因此如何最小化趋近阶段并在此过程中去除抖振仍是研究的热点。

已提出的等速趋近率、指数趋近率和幂次趋近率等实用的滑模趋近率是用来消除系统抖振并保证滑动模态的实现。等速趋近率速度很慢且趋近速度单一;指数趋近率是在等速趋近率基础上增加一指数项,增加了趋近速度,但在接近滑动模态时系统抖振较大;幂次趋近率采用幂次项技术使得系统接近滑动模态时趋近速度变缓,有利于削弱抖振,不足之处是在状态远离滑动模态的趋近阶段存在速度过小、运动时间长的问题[6]。本文采用双幂次趋近率来改善抖振较大的问题，仿真结果表明，双幂次趋近率具有更快的趋近速度和更好的运动品质。

本文针对飞行器的高度及姿态控制设计了滑模控制器,但该控制器使飞行器系统产生的抖振较大,因此在此滑模控制器的基础上作了改进,采用双幂次趋近率设计滑模控制器。仿真结果表明,双幂次趋近率具有更快的趋近速度和更好的运动品质,从而有效减小了系统的抖振。

1　四旋翼飞行器的数学模型

四旋翼飞行器的模型如图1所示。

图1　四旋翼飞行器模型示意图

四旋翼飞行器通过4个螺旋桨产生的推力实现对飞行器的控制。通常采用2种常用坐标系描述四旋翼飞行器,即惯性坐标系和机体坐标系。2种坐标系可以相互转换,从机体坐标系到惯性坐标系的旋转矩阵用R和T表示[7]，具体如下：

以ξ=(x,y,z)表示飞行器在惯性坐标系下的位置,以η=(φ,θ,ψ)表示飞行器的方向角,其中,φ为翻滚角；θ为俯仰角；ψ为偏航角。

以ν=(u,v,w)表示线速度,ω=(p,q,r)表示角速度。假设四旋翼飞行器是均匀对称的刚体,则飞行器受到的2个物理约束条件为:

(1)

(2)

其中,m为飞行器的质量;I为飞行器的惯性矩阵;F为螺旋桨产生的力;τ为力矩。

经过受力分析且综合(1)式和(2)式,推导出飞行器的动力学模型[8]为:

(3)

其中,控制输入U=(U1,U2,U3,U4)；IXX、IYY、IZZ分别为X、Y、Z轴的转动惯量;L为飞行器的质心到旋翼旋转轴之间的距离;g为重力加速度。从飞行器动力学模型中可以看出,四旋翼飞行器是一类欠驱动系统。

2　控制器的设计

四旋翼飞行器的运动可以分解为质心移动和机体转动。惯性坐标系下的机体质心移动依赖于机体侧倾获取的侧向加速度,因此通常的四旋翼控制都通过嵌套的内外环控制实现。内环(姿态环)控制回路的作用是调整飞行器的姿态角,外环(位置环)控制回路的作用是使飞行器按照目标轨迹信号进行飞行或到达期望参考位置。

本文分别设计了飞行器高度控制器和飞行器姿态控制器,控制目标是使系统各个状态在有限时间内达到期望值。

2.1传统PD方法的高度控制

由于高度控制仅考虑z轴方向上的位移,因此只需分析飞行器动力学模型((3)式)中的第3个等式，即

(4)

定义跟踪误差为:

(5)

其中,z为飞行器Z轴方向的位移;zd为飞行器Z轴方向位移的期望值。

根据PD算法有:

(6)

其中,kp、kd为正常数;deZ/dt为对eZ求一阶导数。联合(4)式和(6)式,可求得控制律为:

(7)

2.2基于滑模方法的高度控制

定义滑模面为:

(8)

其中,λ为大于0的常数。在滑模面附近s趋于0,由此可得:

(9)

为使滑模面在平衡点附近达到全局渐进稳定,定义李雅普诺夫函数为:

(10)

其一阶导数为:

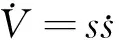
(11)

经数学运算可得:

(12)

(13)

将(4)式代入(13)式得:

(14)

(15)

通过设计控制律U1使(8)式中s在有限时间内达到0。设

(16)

将(16)式代入(15)式,可得:

(17)

(18)

由(17)式和(18)式可以得到:

(19)

令

(20)

其中,ρ为大于0的常数，且ρ>a;sgn(s)=s/|s|,可得:

(21)

(22)

由ρ>a可知ρ-a>0,且在趋于滑模面过程中|s|>0,则由(22)式可得:

(23)

因此滑模控制律U1可以使四旋翼飞行器在有限的时间内达到期望的高度,即

(24)

将(24)式代入(4)式,可得:

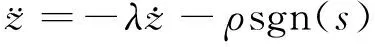
(25)

选择合适的λ和ρ值即可使飞行器在有限的时间内到达期望高度。

2.3姿态控制

针对飞行器的姿态控制，本文设计了一种滑模[9]控制器。以翻滚角为例设计,翻滚角的动力学方程如下：

(26)

定义滑模面为:

(27)

其中,跟踪误差zφ=φ-φd,φ为翻滚角实际值,φd为翻滚角的期望值。

则有:

(28)

(29)

(30)

其中,k1为大于0的常数。

为证明在该控制器作用下飞行器翻滚角在有限的时间内收敛于期望值,定义李雅普诺夫函数为:

(31)

对(31)式两边求导可得:

(32)

所以,在控制律(30)式的作用下,翻滚角将在有限时间内到达滑模面。

滑模控制的主要缺点是抖振较大,为了减小抖振,本文采用双幂次趋近率[10],则(30)式变为:

(33)

其中,α、β、k1、k2均为大于0的常数。

(34)

因此,在控制律(33)式作用下,翻滚角将在有限时间内到达滑模面。

U3和U4的求解方法与U2的求解方法类似,具体求解公式如下：

(35)

3　仿真实验与分析

3.1仿真实验结果

设置的飞行器初始状态为:欧拉角(0.524，0.524，0.524),位置(0，0，0);控制目标为从地面惯性坐标系的原点(0，0，0)到期望的目标位置(1，1，1)并保持悬停。期望偏航角为0。

实际模型参数为:m=0.53 kg,g=9.8 m/s2,IXX=6.228×10-3kg·m2,IYY=6.228×10-3kg·m2,IZZ=1.212×10-2kg·m2,L=0.232 m。

飞行器高度响应曲线如图2所示。图2中,方式1为滑模控制器的高度响应曲线；方式2为传统PD控制方法的高度响应曲线；控制器参数kp=1.6,kd=3。

飞行器3个姿态角响应曲线如图3所示。图3中，方式1为采用双幂次趋近率的滑模控制方法的响应曲线,方式2为采用等速趋近率的滑模控制方法的响应曲线。

图2　高度响应曲线

图3　3个姿态角响应曲线

双幂次趋近率滑模方法和等速趋近率滑模方法的姿态控制律如图4所示。

图4　2种滑模方法的姿态控制律

3.2仿真结果分析

从图2可以得到控制方法的性能比较,见表1所列。

表1　控制方法的性能比较

由表1可以看出,滑模控制器使飞行器在高度方向趋于稳定速度方面优于传统PD控制方法,且超调量较小。

从图3可以看出,采用双幂次趋近率的滑模控制方法有效地减小了系统的抖振,且使系统趋于稳定的速度加快。从图4可以看出,双幂次趋近率的滑模方法姿态控制律的抖振比等速趋近率滑模控制方法的小。

4　结　论

本文针对飞行器的高度控制设计了滑模控制器,由仿真结果可以看出,该控制器使飞行器在高度方向趋于稳定的速度明显优于传统PD控制方法;对于飞行器的姿态控制,设计了采用双幂次趋近率的滑模控制器,由仿真结果可以看出,与采用等速趋近率的滑模控制器相比,该控制器明显减小了系统的抖振。

[1]PATEL A.R，PATEL M A，VYAS D R.Modeling and analysis of quadrotor using sliding mode control[C]//Symposium on System Theory.IEEE，2012:111-114.

[2]GONZALEZ I，SALAZAR S，LOZANO R，et al.Real-time altitude robust controller for a Quad-rotor aircraft using Sliding-mode control technique[C]//International Conference on Unmanned Aircraft Systems.IEEE，2013:650-659.

[3]曹开田.滑模变结构控制理论在飞行器姿态控制系统中的应用研究[D].武汉:武汉大学，2004.

[4]BATEMAN F，NOURA H，OULADSINE M.Fault diagnosis and fault-tolerant control strategy for the aerosonde UAV[J].IEEE Transactions on Aerospace and Electronic Systems，2011，47(3):2119-2137.

[5]杨兴明,高银平，朱建,等.基于分层滑模方法的两轮载人自平衡车的运动控制[J].合肥工业大学学报(自然科学版)，2013，36(12):1456-1460.

[6]张合新，范金锁，孟飞,等.一种新型滑模控制双幂次趋近律[J].控制与决策，2013，28(2):289-293.

[7]杜运磊.无人飞行器航迹规划研究[D].合肥:合肥工业大学，2009.

[8]李航.小型四旋翼飞行器实时控制系统研究[D].大连:大连理工大学，2010.

[9]SHARIFI F，MIRZAEI M，GORDON B W，et al.Fault tolerant control of a quadrotor UAV using sliding mode control[C]//Conference on Control and Fault-Tolerant Systems.IEEE，2010:239-244.

[10]梅红，王勇.快速收敛的机器人滑模变结构控制[J].信息与控制，2009，38(5):552-557.

(责任编辑胡亚敏)

Four rotor aircraft control based on sliding mode controller

YANG Xingming，LI Wenjing

(School of Computer and Information，Hefei University of Technology，Hefei 230009，China)

A kind of sliding mode controller is designed in view of the four rotor aircraft flight control.Firstly，for the height control of four rotor aircraft，a kind of controller based on sliding mode control method is designed，and it is proved that all signals are uniformly bounded eventually according to the Lyapunov stability theory.Secondly，the sliding mode controller is designed for the attitude angle of aircraft，and the stability of it is verified.The double power reaching rates are adopted to reduce the chattering of the controller.Finally，the simulation results show that the designed controller can better control the four rotor aircraft.

four rotor aircraft; sliding mode control; chattering; double power reaching rate

2015-03-26；

2015-07-27

国家自然科学基金资助项目(61100211)

杨兴明(1977-),男,云南安宁人,博士,合肥工业大学副教授,硕士生导师.

10.3969/j.issn.1003-5060.2016.07.012

TP273.5

A

1003-5060(2016)07-0924-05