基于时空检测的城市交通网络瓶颈识别方法研究

丁　恒,　郭　放,　郑小燕,2,　马寒月,　张卫华

(1.合肥工业大学 交通运输工程学院,安徽 合肥　230009; 2.长安大学 公路学院,陕西 西安　710064)



基于时空检测的城市交通网络瓶颈识别方法研究

丁恒1,郭放1,郑小燕1,2,马寒月1,张卫华1

(1.合肥工业大学 交通运输工程学院,安徽 合肥230009; 2.长安大学 公路学院,陕西 西安710064)

为了解决拥堵状态下交通网络瓶颈识别问题,文章基于时空检测数据对道路节点和路段拥堵状态进行了分析,并以此为基础建立了城市交通网络瓶颈识别与分类模型。拥堵发生期间,以任意2辆浮动车连续通过拥堵路径各个交叉口时间间隔作为统计时间,以拥堵路径各个交叉口对应流向流出率作为统计对象,连续统计多辆浮动车通过时的交通量序列,建立了拥堵路径交叉口关联度模型并以此划分交通网络瓶颈。以划分的交通拥堵瓶颈区域作为密闭区域,通过分析拥堵路径平峰期间与拥堵期间的流入流出率,使用切比雪夫不等式在置信度95%范围内建立了拥堵瓶颈的3类模型：输入型瓶颈、输出型瓶颈和通过型瓶颈。以实际区域道路网络为研究对象,使用上述模型对拥堵区域进行了分析,结果表明该模型可有效识别并分类交通网络瓶颈。

交通工程;交通拥堵;时空检测;交通瓶颈;浮动车

0　引　　言

城市化和机动化的发展导致交通拥堵成为诸多城市面临的棘手问题。美国纽约、英国伦敦、法国巴黎、日本东京等城市在20世纪中后期均经历过严重的交通拥堵,虽然此后采用各种交通工程改善手段使交通拥堵有所缓解,但至今仍难以真正摆脱拥堵的困扰。在我国,近年来大面积交通拥堵时常发生,居民出行时间和燃油消耗都出现了大幅度的增长。因此缓解交通拥堵受到了交通行业专家和学者的广泛重视,已有研究采用收费管理[1]、交通控制[2]、网络平衡[3]等手段来解决交通拥堵问题,但上述研究都是解决拥堵形成状态下的交通管理问题,而没有对道路交通瓶颈识别问题展开研究。

关于交通拥堵瓶颈的定义,美国道路通行能力手册以常发性路段行车速度小于22 km/h作为界定标准,而我国的界定规则为车辆在3个周期内仍未通过的信号交叉口或排队长度超过1 km的道路路段[4]。上述交通拥堵界定方法针对城区道路微观区域,在实际交通管理中具有较好的可操作性,但缺乏理论依据。在交通拥堵微观瓶颈研究方面,以快速路为研究对象,Helbing在与 Kerner争论交通流基本图时已进行了详细探讨[5-7]。文献[8]以入口匝道为研究对象,分析快速路网瓶颈存在早发性失效问题。微观瓶颈研究的对象涉及面小、针对性强,但不能直接用于复杂的城市交通网络瓶颈的界定。

交通网络瓶颈研究主要有2大思路:① 采用复杂网络理论对城市道路状态进行分析,如文献[9]研究假定的各个网络节点特征参数较为一致,通常只能用来分析运行具有相对独立性的城市快速路,很难分析交叉口类型各异的城市交通网络;② 依据道路网络实际通行能力,分析城市道路网络瓶颈识别方法[10-12]，由于受到传统固定交通检测手段的限制,导致网络交通瓶颈的分析类似于微观瓶颈的简单叠加,缺乏微观瓶颈间有效的交通流量相关分析。随着交通流量检测手段的多样化,文献[13]以速度差作为参考阈值提出了三相位时空交通瓶颈决策模型,由于城市道路交叉口间距离较近,过饱和状态下路段上、下游行驶车速差值不大,该模型精度值得商榷。

准确把握城市道路网络瓶颈的识别问题中,有效的时空数据检测是重要基础。本文依据浮动车数据(floating car data,FCD)和固定检测器的时空检测数据,在城市路网流量、流向和特征参数分析的基础上,提出了一种城市交通网络瓶颈识别方法。该方法不仅能用来分析瓶颈区域,还可针对拥堵特征进行分类。

1　道路网络时空检测与瓶颈识别

(1) 城市道路网络时空检测方法。最常见的交通流量检测方法是固定检测,该方法易于检测断面交通流量、车速及排队长度等参数,但是对于区域路网的交通量分布、车速分布及路段行程时间检测较为困难。基于FCD的空间检测可以弥补固定检测方法的不足,并能有效地获取交通路网中车速、平均行程时间和交通量等数据。结合两者特点,采用浮动车和固定检测器检测拥堵路网各个路段及交叉口的时空数据,再依据电子地图数据即可判别路网运行状态。具体道路网交通量数据检测及处理流程如图1所示。

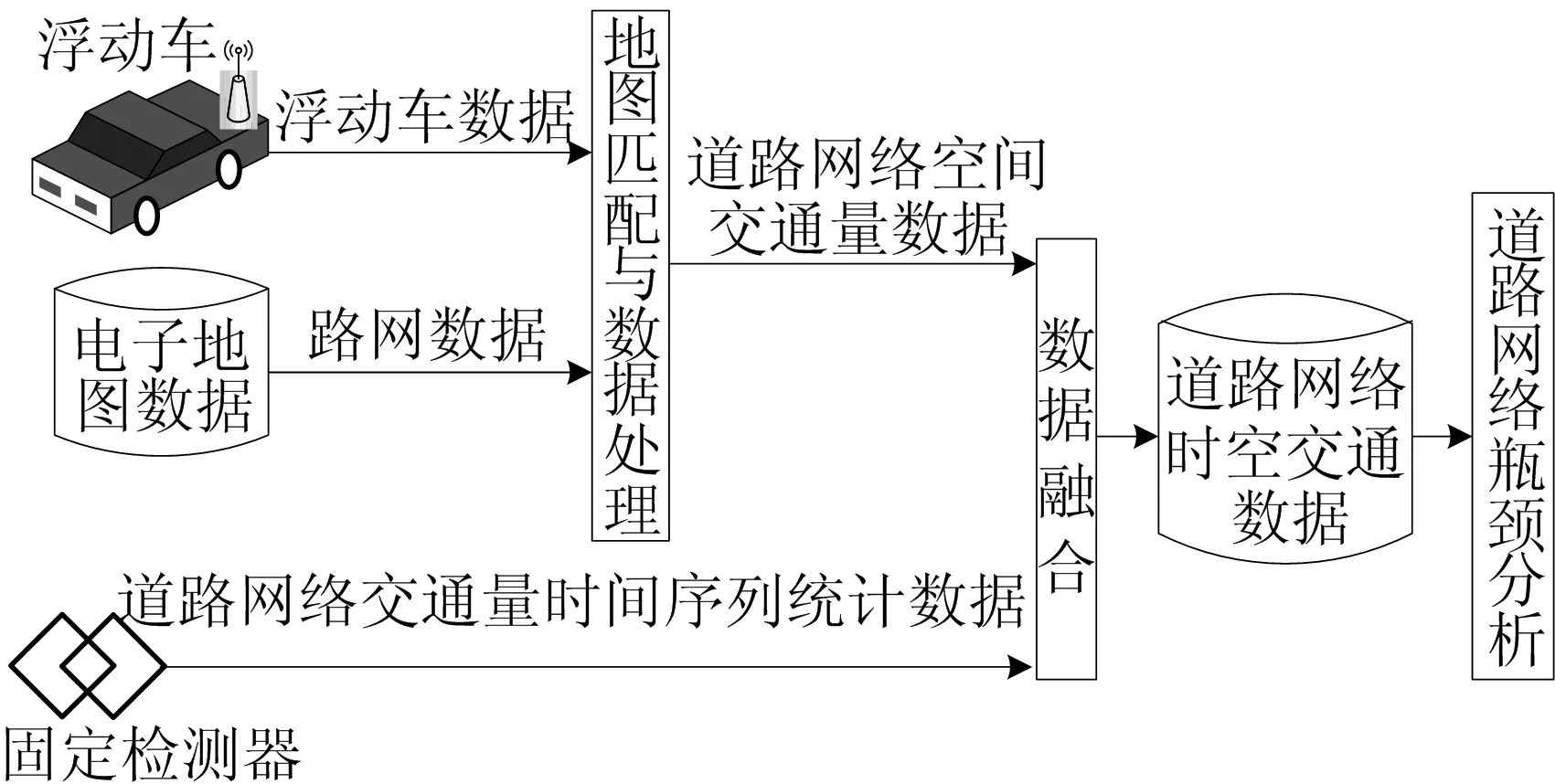
图1　道路网络时空数据检测及处理流程

(2) 城市交通网络瓶颈识别。受城市土地利用性质的影响,城市交通网络拥堵呈现一定的潮汐性和周期性。根据拥堵交通路网流量流向可分为通过型交通拥堵和源发型交通拥堵。通过型交通拥堵主要发生在城市组团之间的道路网,而源发型交通拥堵主要发生在土地开发强度较高的区域路网。结合路网交通拥堵分类,网络交通瓶颈除具有微观交通瓶颈中需求超过供给能力的特点外,还应包括以下2点:① 导致路网发生拥堵的交通需求具有一致性;② 引发路网拥堵的各个节点交通量具有较强的相关性。针对网络交通瓶颈的特点,依据城市道路网络时空检测数据初步划分交通拥堵区,通过拥堵交叉口流量流向的相关性分析、决策,进一步确定交通瓶颈范围,并以此为基础对交通瓶颈类型进行分析。

2　道路路段及交叉口拥堵状态分析

城市道路路段是一个相对独立的区域,利用在对应路段FCD的行程速度分布即可有效获取路段状态,因此本文对道路路段拥堵不再赘述。

交叉口交通拥堵可分为2种状态:① 交叉口总交通需求超过交叉口通行能力,即交叉口过饱和拥堵,这种情况下调整信号配时无法满足通行需求;② 交叉口某一方向交通需求超过该流向通行能力,存在非对称交通流[14]，即流向过饱和拥堵,这种情况下由于交叉口只有部分流向拥堵,一般可通过优化信号配时满足拥堵流向通行需求,也可能通过调整信号配时仍无法满足通行需求。

2.1交叉口过饱和拥堵

交叉口过饱和拥堵可表示为交叉口总的交通需求qTD超过交叉口通行能力qc,即

(1)然而,城市道路交叉口绝大多数为信号控制交叉口,qc显著受到信号配时方案的影响。因此(1)式很难用来分析实际交叉口拥堵状态。

根据交叉口拥堵及信号控制的规律,当饱和度达到0.9时,交叉口已经处于拥堵状态。在考虑信号周期及拥堵时间约束条件C=C0和t≥τ时,(1)式可以表达为

(2)其中,qi为第i相位到达交通量;Si为第i相位通行时车道饱和流量和;λi为第i相位绿信比;N为相位数量;C为信号周期;C0为最佳信号周期;t为拥堵持续时间;τ为拥堵时间决策阈值,可采用1个诱导周期时长或3个以上周期C时长,一般取值为5～10 min。

2.2流向过饱和拥堵

流向过饱和拥堵是指交叉口某一流向流量处于拥堵状态,可采用流向通行能力或流向通行延误来表示。

(1) 流向通行能力过饱和拥堵。流向过饱和拥堵可简单表示为交叉口某一流向i交通需求qCD(i)超过该流向通行能力qc(i),即

(3)参考(2)式,在考虑信号周期及拥堵时间约束条件C=C0和t≥τ时,(3)式可以表示为

(4)在发生交通拥堵特别是溢流状况下,交叉口某一流向i实际通行能力不仅受到进口车道的限制,还可能受到出口通行能力的限制,文献[15]提出以流出率计算拥堵交叉口通行能力模型,在考虑信号周期及拥堵时间约束条件C=C0和t≥τ时,(3)式可以表达为

(5)在一定的交通渠化及信号配时条件下,根据交叉口流向流量,流向通行能力过饱和拥堵可以进行验证。

(2) 流向延误过饱和拥堵。以交叉口某流向车辆平均延误作为参考指标,根据交叉口类型,当该流向车辆平均延误较高导致的该流向服务水平等级处于E级或F级时，即可认为该流向处于过饱和拥堵状态。流向车辆延误计算方法[15]为

(6)其中,di为交叉口第i流向车辆平均延误;ge(i)为第i流向信号相位有效绿灯时间;X为第i流向饱和度;T为分析时长;d0为第i流向初始排队延误。

流向延误过饱和拥堵的计算过程比流向通行能力过饱和拥堵的更复杂,但是流向延误计算能较好地体现车辆在信号交叉口的受阻状况,易通过在该流向通行的浮动车延误数据进行验证。通过上述拥堵状态分析,以连片道路路段及交叉口区域作为初步划分的交通拥堵区域。

脑出血(ICH)是指脑实质内的出血,以高血压动脉粥样硬化出血最为多见[1]。我国的ICH患者主要是由高血压病诱发,所以我国一直沿用高血压脑出血的诊断。高血压脑出血的发病年龄为25~85岁,男性的发病率略高于女性[2]。随机抽选我院收治的50例高血压脑出血患者资料作为研究对象,以探究高血压脑出血的外科临床护理干预效果。报道如下。

3　拥堵交叉口关联度分析

虽然通过初步划分的交通拥堵瓶颈区内交叉口及道路路段均处于拥堵状态,但不能表明拥堵区内各个交叉口、各种流量流向均处于拥堵状态,且部分交叉口因自身通行条件等原因是孤立型的交通拥堵点,与其他交叉口并不存在必然联系。从交通管理需求的角度来看,因自身条件造成的孤立型拥堵交叉口必须单独进行优化改造设计,因此有必要在划分网络交通瓶颈区域时剥离这些孤立型拥堵交叉口。

交通拥堵区拥堵路径分布如图2所示,其中E、W、S、N表示交叉口东、西、南、北4个方向。假设经初步划分的交通瓶颈拥堵路径为：O点→(l,k)交叉口→(l+1,k)交叉口→(l+1,k+1)交叉口→(m-1,n)交叉口→(m,n)交叉口→D点,路径经过的交叉口数量有J个,在不经绕行的情况下,显然有

(7)

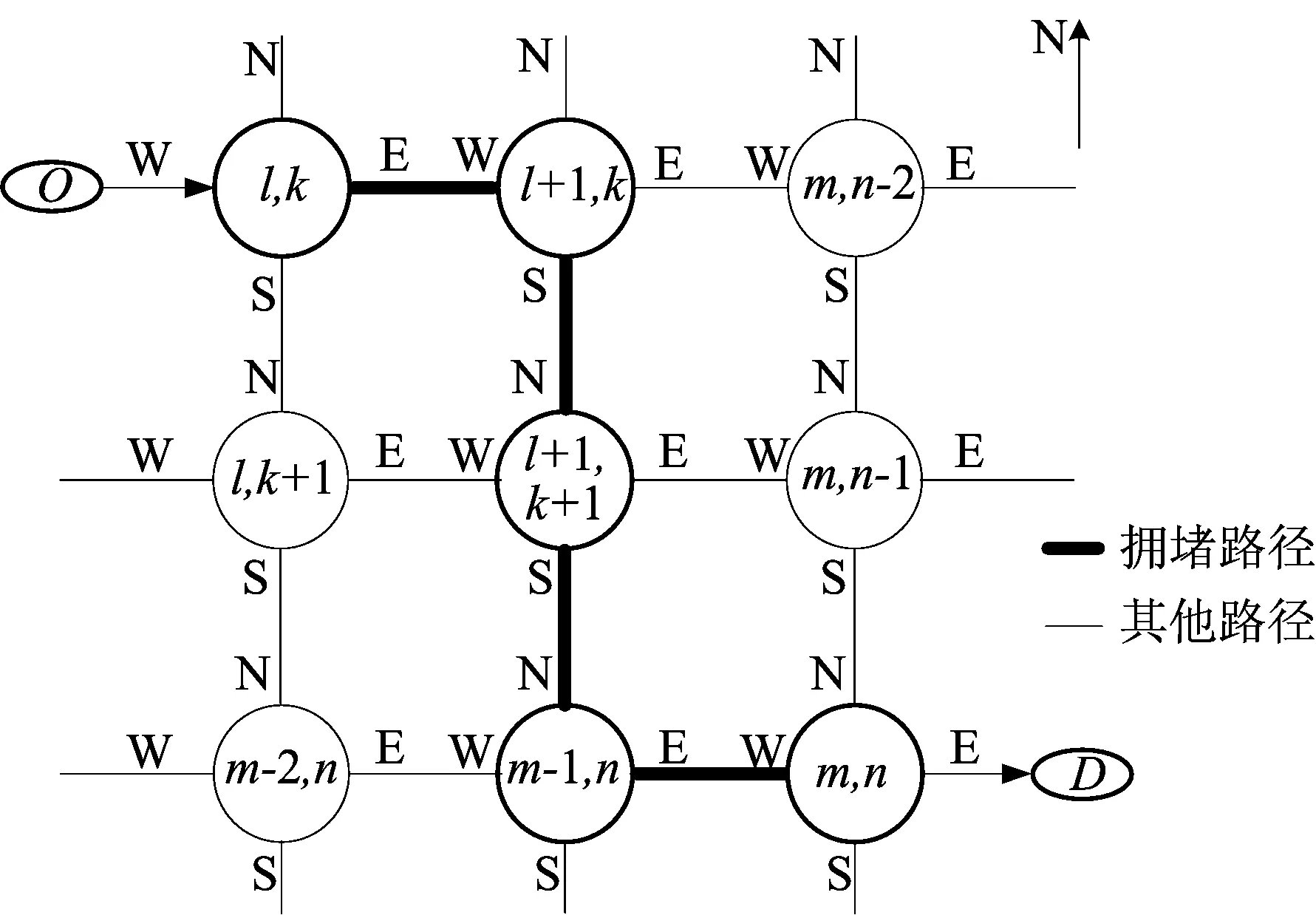
图2　交通拥堵区拥堵路径分布

若在拥堵分析时间内有y辆浮动车经过该路径,浮动车通过J个交叉口行程时距如图3所示,由图3可统计浮动车通过交叉口时交通量的流出情况。

图3　浮动车行程时距图

(8)其中,qWE,out(l,k)为交叉口(l,k)由西向东的流出率。则y辆浮动车在统计时间内通过交叉口(l,k)序列可表示为{Q(l,k)(WE,j→j+1)}1≤j≤y-1。

同理,可获得2辆浮动车通过交叉口(l+1,k)经路径O→D流入交叉口(l+1,k+1)的交通量为

(9)其中,qWS,out(l+1,k)为交叉口(l+1,k)由西进口向南的流出率。

y辆浮动车连续通过交叉口(l+1,k)统计序列为{Q(l+1,k)(WS,j→j+1)}1≤j≤y-1。浮动车经过其他交叉口数据以此类推。若存在2辆浮动车连续通过O→D路径各个交叉口的时间间隔较接近时,仅选择第j辆或第j+1辆作为有效浮动车,将第j辆至第j+1浮动车之间检测的交通量数据累计到临近的浮动车检测数据中，具体如下：

(10)其中,o为整数,且min(l,m)≤o≤max(l,m);p为整数,且min(k,n)≤p≤max(k,n);g(o,p)(i)为浮动车通过路径O→D交叉口(o,p)时对应流向信号绿灯时间。

在没有合并数据的条件下,通过y辆浮动车检测数据,可得J个交叉口交通流量序列矩阵为:

(11)

拥堵区域交叉口的相关度可通过Θ求解相关系数矩阵,步骤为:对Θ进行标准化转换,得到标准化矩阵θ后,相关系数矩阵即为θ和θ转置θ′的乘积，即

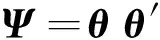
(12)

其中,Ψ为相关系数矩阵,是下三角矩阵。

如果矩阵对角线下方的相关系数低于一定阈值(建议取值为0.9),则认为该相关系数所在的行和列所在的两交叉口交通流量相关度不高,即交通拥堵并非相互影响关系。以本文划分的初始拥堵瓶颈为基础,通过交叉口间关联度分析,可进一步确定交通网络瓶颈。

4　道路网络瓶颈类型分析

网络瓶颈中可能存在多条拥堵路径,受城市土地利用与出行结构的影响,在拥堵期间拥堵路径交通在流向上也呈现一定的分布规律。将网络瓶颈作为一密闭区域,通过拥堵路径相对网络瓶颈的流入流出交通量可分析路网拥堵成因,从而可划分拥堵类型。以网络瓶颈中拥堵路径为分析对象,统计平峰期间该路径驶入驶出交通流量,即

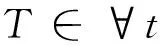
(13)

(14)

其中,t(m,n)(1)为y辆浮动车中第1辆浮动车通过交叉口(m,n)的时间;t(m,n)(y)为第y辆浮动车通过交叉口(m,n)的时间;t(l,k)(1)为y辆浮动车中第1辆浮动车通过交叉口(l,k)的时间;t(l,k)(y)为第y辆浮动车通过交叉口(l,k)的时间。

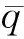
(15)

(16)

其中,ε∈R+。

在置信度为95%条件下,可得ε=4.472δ。交通瓶颈分类模型如下:

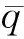
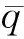
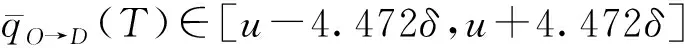
5　实例分析

现以某市高峰期间一个区域拥堵路网来确定交通网络瓶颈的计算过程。道路网络结构如图4所示,路网内有城市快速路(屯溪路、金寨路)、主干道(徽州大道、芜湖路)和次干道(桐城路、宁国路等)。地面车辆检测器检测的拥堵路网及临近交叉口流量流向数据见表1所列。

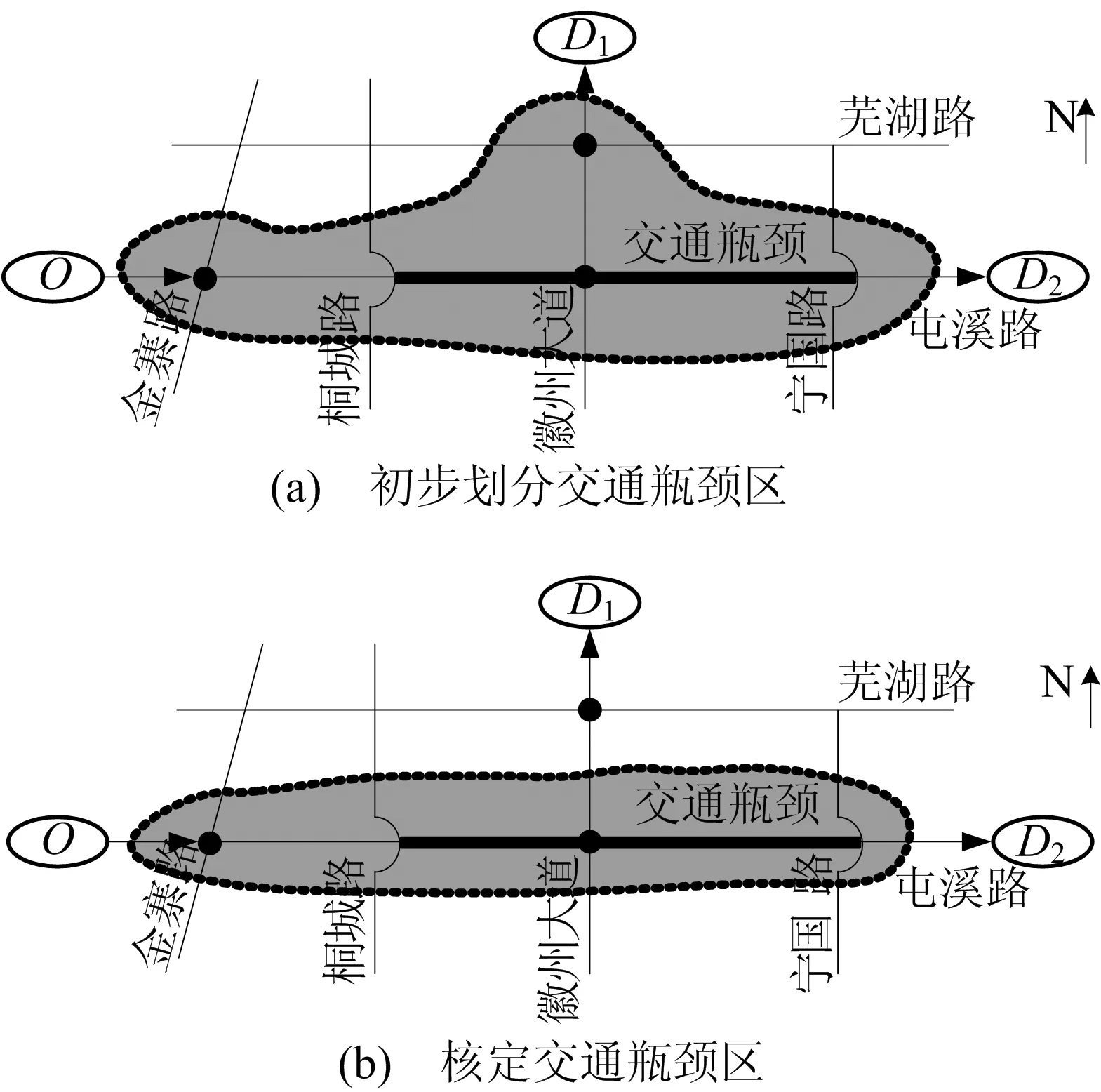
图4　交通瓶颈区划分图

表1　拥堵区域交叉口高峰流量 pcu/h

注:屯溪路规划为城市快速路,桐城路和宁国路均下穿屯溪路,这2个交叉口均无左转交通量。

(1) 交通拥堵瓶颈识别。采用(2)式计算,发现徽州大道与芜湖路交叉口处于过饱和拥堵状态。根据交叉口流量流向与通行能力,直接采用(4)式进行计算。处于流向过饱和拥堵的交叉口有:金寨路与屯溪路交叉口西直行、徽州大道与屯溪路交叉口西直行和左转、徽州大道与芜湖路交叉口南直行和北左转,此外屯溪路(桐城路至宁国

路段)处于过饱和拥堵状态。根据路段和交叉口拥堵状态,在区域路网上存在2条拥堵路径,分别为O→D1和O→D2,初步划分的交通瓶颈区如图4a所示。根据(11)式,统计近2个诱导周期发生交通拥堵期间浮动车通过各交叉口交通流量数据。通过路径O→D1共有11辆浮动车,路径O→D1经过的交叉口对应流向交通量矩阵ΘO→D1为:

(17)

采用(12)式计算可得相关系数矩阵ΨO→D1为:

(18)徽州大道与芜湖路交叉口的交通量与其他交叉口相关系数显著低于0.9,显然该交叉口与其他交叉口拥堵相关性较低。同理,通过路径O→D2共计有16辆浮动车,经过的交叉口对应流向交通量矩阵ΘO→D2和相关系数矩阵ΨO→D2分别为:

(19)

该路径所有交叉口交通量相关系数均高于0.9,O→D2可考虑为统一的拥堵路径。经过相关系数分析后,确定的交通瓶颈区域如图4b所示。

6　结　　论

本方研究结果表明:

(1) 基于交叉口的流量流向和通行能力,建立的交叉口状态分析模型可较好地把握交叉口的拥堵状态。

(2) 以浮动车连续通过拥堵路径时交叉口对应流向流量数据为参考,以0.9为相关系数阈值的拥堵路径交叉口关联度的分析可有效划分交通拥堵瓶颈区。

(3) 使用切比雪夫不等式,通过比较拥堵期间与平峰期间的拥堵路径驶入驶出交通量,在置信度为95%条件下,可有效分类区域路网拥堵瓶颈。

由于受到实际检测条件的限制,本文仅针对局部道路网络采用文中建立的拥堵瓶颈识别与分类模型进行了验证。对于大范围的城市交通网络,计算过程类似,但是随着路网规模的不断扩大,拥堵路径交叉口数量急剧增长,计算相关系数矩阵时,计算量将大幅度增加,具体复杂程度还有待进一步验证。

[1]ZHANG X N,VAN WEE B.Enhancing transportation network capacity by congestion pricing with simultaneous toll location and toll level optimization [J].Engineering Optimization,2012,44(4)：477-488.

[2]KERNER B S.Control of spatiotemporal congested traffic patterns at highway bottlenecks [J].Physica A：Statistical Mechanics and its Applications,2005,355(2/3/4)：565-601.

[3]YANG H,HUANG H J.The multi-class,multi-criteria traffic network equilibrium and systems optimum problem [J].Transportation Research Part B：Methodological,2004,38(1)：1-15.

[4]陈万鑫.城市道路瓶颈交叉口识别及解决方案研究[D].长春:吉林大学,2013.

[5]KERNER B S.Three-phase traffic theory and highway capacity [J].Physica A：Statistical Mechanics and its Applications,2004,333：379-440.

[7]TREIBER M,KESTING A,HELBING D.Three-phase traffic theory and two-phase models with a fundamental diagram in the light of empirical stylized facts[J].Transportation Research Part B：Methodological,2010,44(8/9)：983-1000.

[8]SUN J,ZHANG J,ZHANG H M.Investigation of the early-onset breakdown phenomenon at urban expressway bottlenecks in Shanghai [J].Transportmetrica B：Transport Dynamics,2014：2(3):215-228.

[9]陈绍宽,韦伟,毛保华,等.基于改进时空Moran’sI指数的道路交通状态特征分析[J].物理学报,2013,62(14):148901-1-7.

[10]邓瑞.城市区域路网交通瓶颈识别与预测[D].成都:西南交通大学,2012.

[11]赵月,杜文,陈爽.复杂网络理论在城市交通网络分析中的应用[J].城市交通,2009,7(1)：57-65.

[13]LEE W H,TSENG S S,SHIEH J L,et al.Discovering traffic bottlenecks in an urban network by spatiotemporal data mining on location-based services[J].IEEE Transactions on Intelligent Transportation Systems,2011,12(4):1047-1056.

[14]丁恒，郑小燕，张卫华.基于伴随相位的非对称交通流交通信号改善研究[J].合肥工业大学学报(自然科学版)，2008，31(3)：356-359.

[15]Transportation Research Board Business Office.Highway capacity manual 2010[R].Washington D C：Transportation Research Board of the National Academies,2010.

(责任编辑胡亚敏)

Urban traffic network bottleneck identification based on temporal and spatial detection

DING Heng1, GUO Fang1, ZHENG Xiaoyan1,2, MA Hanyue1, ZHANG Weihua1

(1.School of Transportation Engineering, Hefei University of Technology, Hefei 230009, China; 2.School of Highway, Chang’an University, Xi’an 710064, China)

In order to solve the problem of bottleneck identification in congested traffic network, the road node and link were analyzed based on temporal and spatial detection data, and then the urban traffic network bottleneck identification and classification model was established. Taking the interval of any two floating cars continuously through each intersection of congestion path as statistical time and the rate of outflow corresponding to each intersection of congestion path as statistical object, the traffic sequence when many floating cars were passing through was continuously statisticalized. Then the intersection correlation model was established to divide the traffic network bottleneck. Taking the divided area of traffic bottleneck as a closed area, through analyzing the inflow and outflow rate during the period of congestion and flat peak, and using the Chebyshev’s inequality under the condition of a 95% confidence level, three types of congestion bottleneck were established, namely imported bottleneck, outputted bottleneck and passed bottleneck. Taking the actual regional road network as analysis object, the congestion area was analyzed by using the above model. The results show that the model can effectively identify and classify the traffic network bottleneck.

traffic engineering; traffic congestion; temporal and spatial detection; traffic bottleneck; floating car

2015-03-17；

2015-05-08

国家自然科学基金资助项目(61304195；51178158;51578207；51308176);安徽省自然科学基金资助项目(1408085QF111)

丁恒(1980-),男,安徽阜南人,博士,合肥工业大学副教授,硕士生导师;

张卫华(1967-),男,安徽宿松人,博士,合肥工业大学教授,博士生导师.

10.3969/j.issn.1003-5060.2016.07.002

U491.4

A

1003-5060(2016)07-0868-07