电场活化聚合物变形特性有限元分析
2016-09-27陈娟,刘焜
陈 娟, 刘 焜
(合肥工业大学 机械与汽车工程学院,安徽 合肥 230009)
电场活化聚合物变形特性有限元分析
陈娟,刘焜
(合肥工业大学 机械与汽车工程学院,安徽 合肥230009)
电场活化聚合物(dielectric elastomer,DE)是一种高分子聚合物薄膜材料,该材料在电场力作用下会产生超弹性变形,且具有非线性特性。文章应用ANSYS有限元仿真分析方法,选取最适用的Ogden模型材料参数作为模型参数,通过对模型其他参数和边界的设定,构建出DE变形机理有限元模型;通过仿真实验对比分析了材料变形特性规律及影响因素,即驱动电压的变化、预拉伸的大小以及电极材料等因素影响着DE应变的响应。有限元仿真分析方法为DE变形机理特性研究提供了一种可行的创新方法。
电场活化聚合物;ANSYS软件;变形特性;Ogden模型
0 引 言
电场活化聚合物(dielectric elastomer,DE)是基于Maxwell效应下的一种新型功能材料[1],具有很好的柔顺性和仿生性能,可以产生380%的应变[2-4]。DE没有抗弯、抗压能力,完全依靠外部施加的预拉力保持其形状[5]。这种材料承受载荷时具有明显的非线性。
为了深入研究DE的变形机理,国内外学者相继开展了一些研究。文献[3]研究结果显示,对DE进行300%双轴预拉伸,电致驱动变形可达到100%;文献[6]说明了预拉伸后的DE将产生更大的电致驱动变形,综合考虑预拉伸等因素的影响,提出了DE产生超大变形的机理;文献[7]提出DE的不同模型,研究出当材料产生失效时驱动模式过渡过程中有助于产生更大的电致变形理论。然而针对非线性大变形材料,只从实验中得出结果是不全面的。国内外研究人员致力于相关基础理论和大量实验的研究来获取DE的形变影响因素和变形机理规律,并积累了大量的实验经验。
目前用数值分析方法来描述DE变形机理特性的研究较少,而在各种数值分析方法中,有限元法原理简单、灵活、通用,特别是在非线性有限元分析的基础上进行线性分析,能解决非线性大变形的问题。本文应用ANSYS有限元仿真分析方法来描述DE的变形特性及其影响因素。
1 试验方案
(1) 试验目的。通过试验方法获取DE变形规律及影响因素。
(2) 试验材料。材料为HN-1110T(韩国Hannam Hi-Tech公司);电极材料为导电膏(黑色膏状);辅助材料为绝缘板、绝缘胶布、导线、0.2 mA保险丝。
(3) 试验过程如下:① 组建实验平台,确保实验方案正确有效地实施,实验现场如图1a所示;② 制作夹具,如图1b所示,通过夹具将薄膜样品按一定比例拉伸后固定在绝缘装置上;③ 缓慢均匀地施加电压,观察薄膜材料变形现象,选取关键时刻点的电压值,直到薄膜被击穿破裂,关闭电压源。

图1 试验系统
(4) 试验方法。试验中用数码相机记录变形过程,基于B样条小波的图像边缘检测技术对后续的图像进行处理[8],再利用AutoCAD软件自带的计算功能,计算出DE变形前、后区域的面积和长度,经过数据处理计算出材料的应变率。
2 构建有限元模型
2.1模型分析
采用有限元分析方法是为了准确地描述DE的非线性大变形行为,为了简化计算,假设材料具有不可压缩、均匀和各向同性等力学特性,则通常以应变能密度函数W作为理论基础[9]。
根据DE的变形规律,将仿真过程分预拉伸和施加载荷2个阶段。建立有限元模型,模型规格分别为φ20 mm×1.1 mm和20 mm×20 mm×1.1 mm,首先沿着X、Y方向进行均匀预拉伸(100%×100%)和不均匀预拉伸(100%×200%),然后在拉伸变形后施加载荷。其中划分网格后总单元数为4 200个,节点为17 000个。选择Element Type下add/edit/delete定义单元为三维实体Solid186,设定弹性模量为0.8 MPa,泊松比为0.49,密度为1 000 kg/m3。选取3个参数的Ogden参数数值,分析自由边界条件拉伸,即在DE边界没有施加任何约束。有限元模型如图2所示。
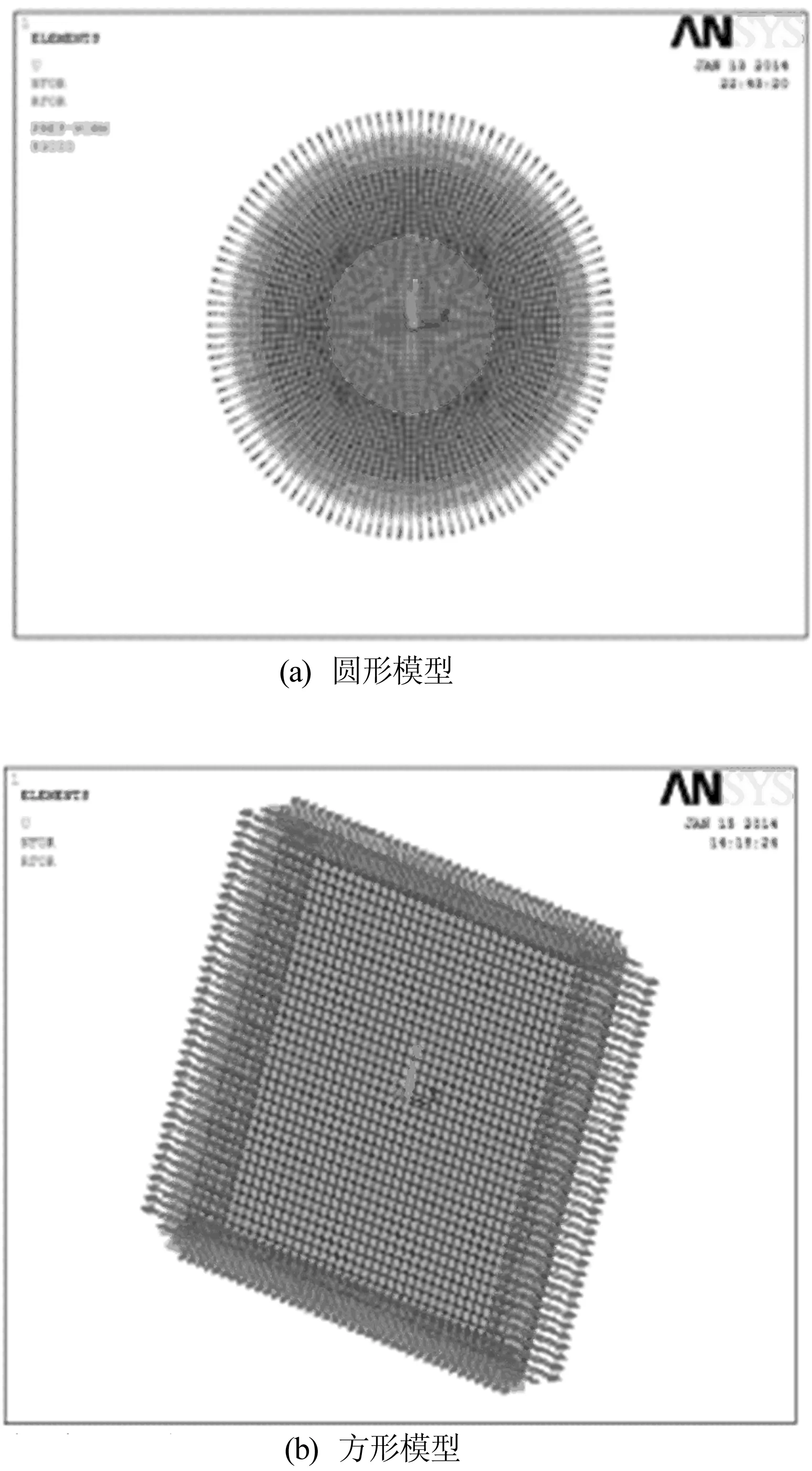
图2 有限元模型
通常解决变形率较大的材料,Ogden能够提供最佳近似解,它适用的应变水平高达700%,并且具有高价的参数可以提供准确的解决方案。根据超弹性理论中Ogden模型[10],数据拟合后获取的材料参数作为本文DE变形机理的理论模型数据,其本构模型方程为:
(1)
其中,μi、αi为待定材料常数,由试验拟合的数据见表1所列。
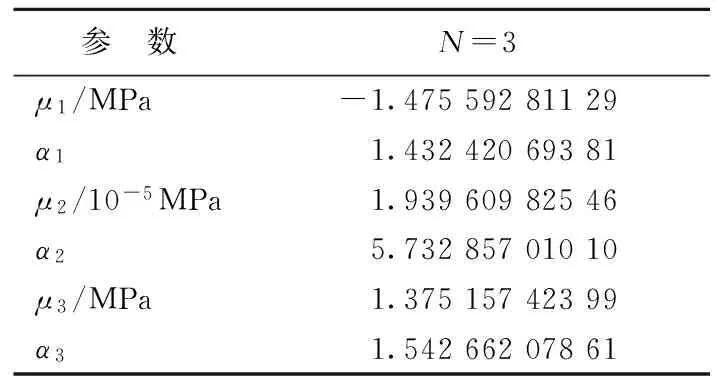
表1 Ogden模型拟合数据
2.2薄膜受力分析
DE材料是具有不可压缩特性的薄膜材料,在进行有限元分析时需要考虑载荷作用下薄膜结构的变形和内力的变化。薄膜材料的应力状态可分为拉伸纯状态、褶皱状态、松弛状态3种[11-13]。为研究材料的变形规律,需要设定薄膜材料内的主应力为σ1和σ2(σ2≤σ1),主应变为ε1和ε2(ε2≤ε1)。为了得到当前状态的压力,通过Cauchy应力、主应力来计算Cauchy应力分量,即
(2)
(3)
再将Green应变转换为ε={εx,εy,εz},则有:
(4)
(5)
由(2)~(5)式可知,二维应力应变状态表明,当σ1和σ2都大于0时,薄膜材料拉伸张紧;当σ1>0、σ2≤0、ε1>0时,薄膜材料在σ2方向产生褶皱;当ε1和ε2都小于等于0时,薄膜材料完全松弛。从上述分析可知,对于电场活化聚合薄膜变形机理采用有限元方法进行研究,只需考虑第1种和第2种状态。
3 有限元仿真结果及分析
3.1预拉伸结果
文献[14-15]指出,预拉伸大小对薄膜材料的变形有很大影响。本次模拟试验通过ANSYS有限元软件将预拉伸与变形率作为主要研究内容,预拉伸状态分别考虑了如下2种情况。
(1) 均匀预拉伸。根据试验结果得知,薄膜在随着拉伸逐渐增大,材料沿着柱面半径方向不断延展,均匀预拉伸后DE薄膜的位移云图如图3所示,薄膜材料在均匀预拉伸的情况下沿着柱面坐标的半径方向最大位移延展了10.326 mm。由于薄膜材料表面均匀拉伸,材料沿各个方向产生的应力是均匀的。
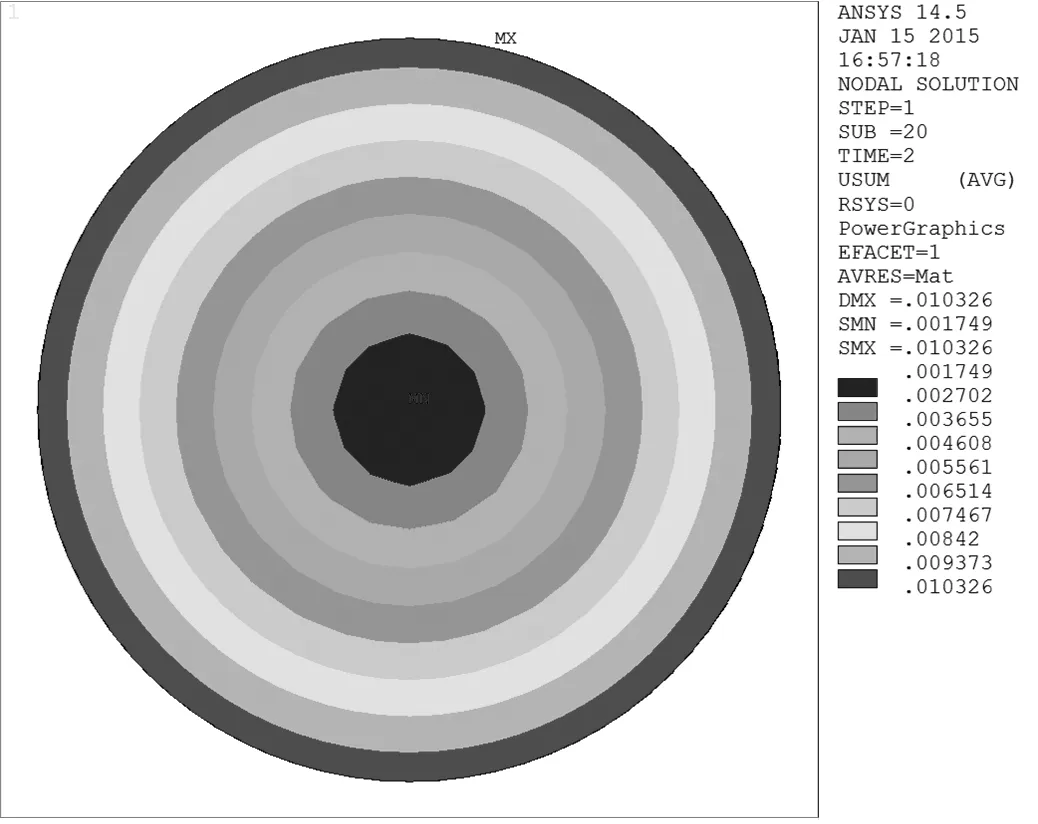
图3 均匀预拉伸后DE薄膜的位移云图
(2) 不均匀预拉伸。选取的薄膜材料原始尺寸为20 mm×20 mm,对材料进行不均匀预拉伸200%×100%(X方向200%拉伸,Y方向100%拉伸),模拟结果如图4所示。

图4 不均匀预拉伸后DE薄膜的位移云图
由图4可知,当X、Y方向预拉伸比例不同时,薄膜材料在电场中的变形方向也是沿着柱面半径,薄膜在X方向最大位移为20 mm,Y方向最大位移为10 mm,说明不均匀预拉伸对材料的变形起到了一定的阻碍作用。
3.2施加载荷结果
在预拉伸基础上,边界条件在X、Y方向施加不同的预拉伸,当电场作用在薄膜表面时,其边界自由度全部约束。结果表明,当薄膜均匀预拉伸后施加载荷,薄膜表面承受的力是均匀的,DE表面受到的最大电压为5 500 V,而静电压力为0.095 8 Pa,薄膜材料沿半径方向位移延展了7.293 mm,电场聚合物变形率为36.47%,输出位移云图和等效应力云图如图5所示。

图5 圆形薄膜均匀预拉伸后位移和等效应力云图
不均匀预拉伸后对薄膜进行加载,对圆形薄膜材料延展比例不同的2个方向施加同样的载荷,仿真结果显示,薄膜表面出现褶皱现象,褶皱的纹理朝着预拉伸较小的方向,并且图像呈现椭圆形状倾向,如图6所示。
由图6可以看出,X方向的位移延展了6.04 mm,Y方向的位移延展了5.04 mm,X方向的变形率为30.2%,Y方向的变形率为25.2%。这充分说明了预拉伸是衡量和控制材料变形的决定性因素。
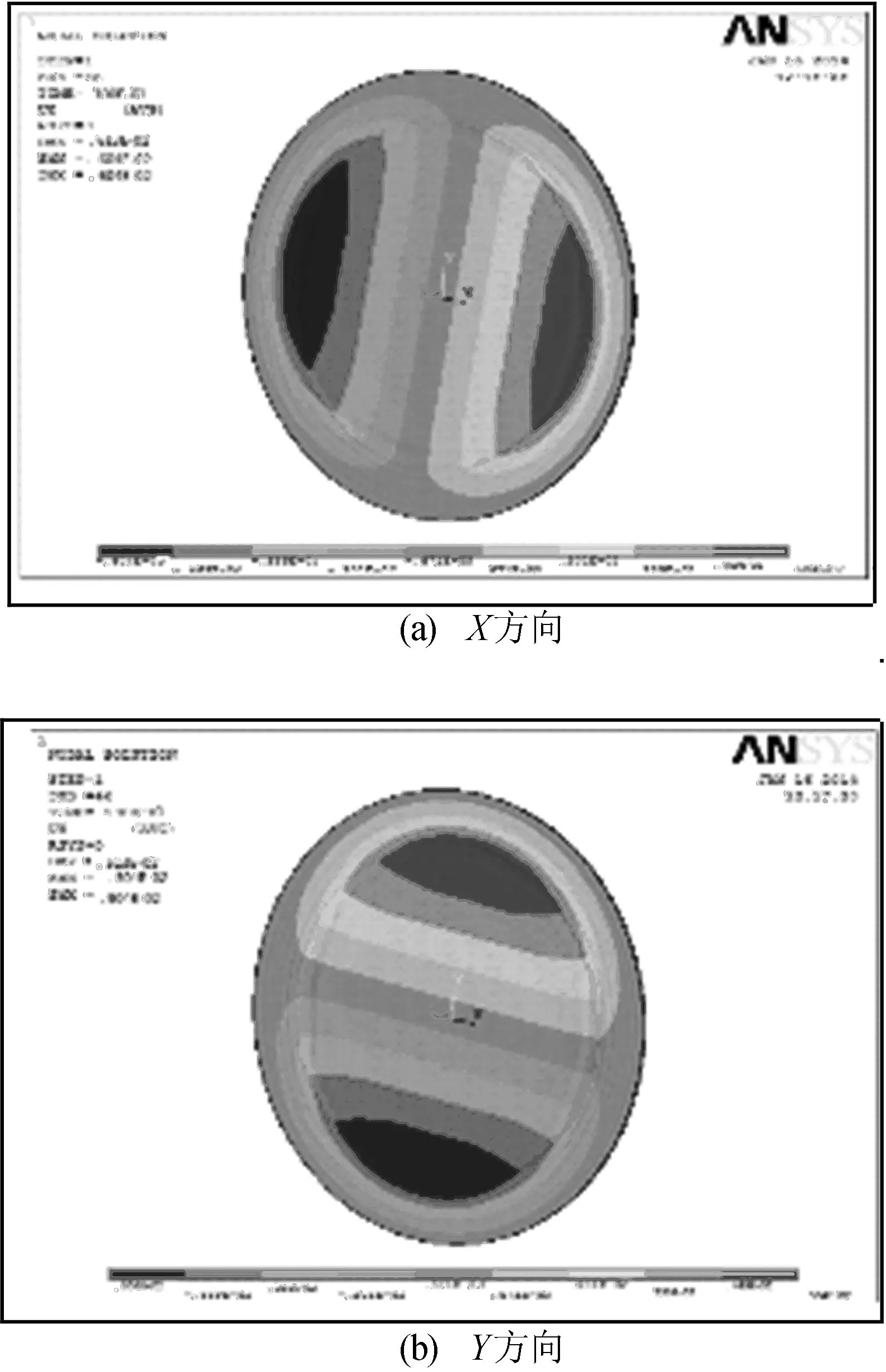
图6 圆形薄膜不均匀预拉伸后位移云图
4 结果讨论
4.1预拉伸对应变的影响
不同的预拉伸情况下模拟值与试验值的比较如图7所示。
从数值分析和实验结果可以看出,随着电压的增加,应变的速度都逐步增加;在自由边界条件下,电压范围小,随着电压的增加,材料的应变响应慢,高电压范围内特别是在3 000~4 000 V时,材料应变响应快速增长。从对比结果来看,仿真结果略小于试验结果,因为在有限元分析中,对模型施加的是一个恒定压力,而薄膜材料具有黏弹性,存在蠕变现象,特别是在施加4 000 V以上电压时非线性特别明显,导致有限元分析的输出变形与试验结果存在一些差异。

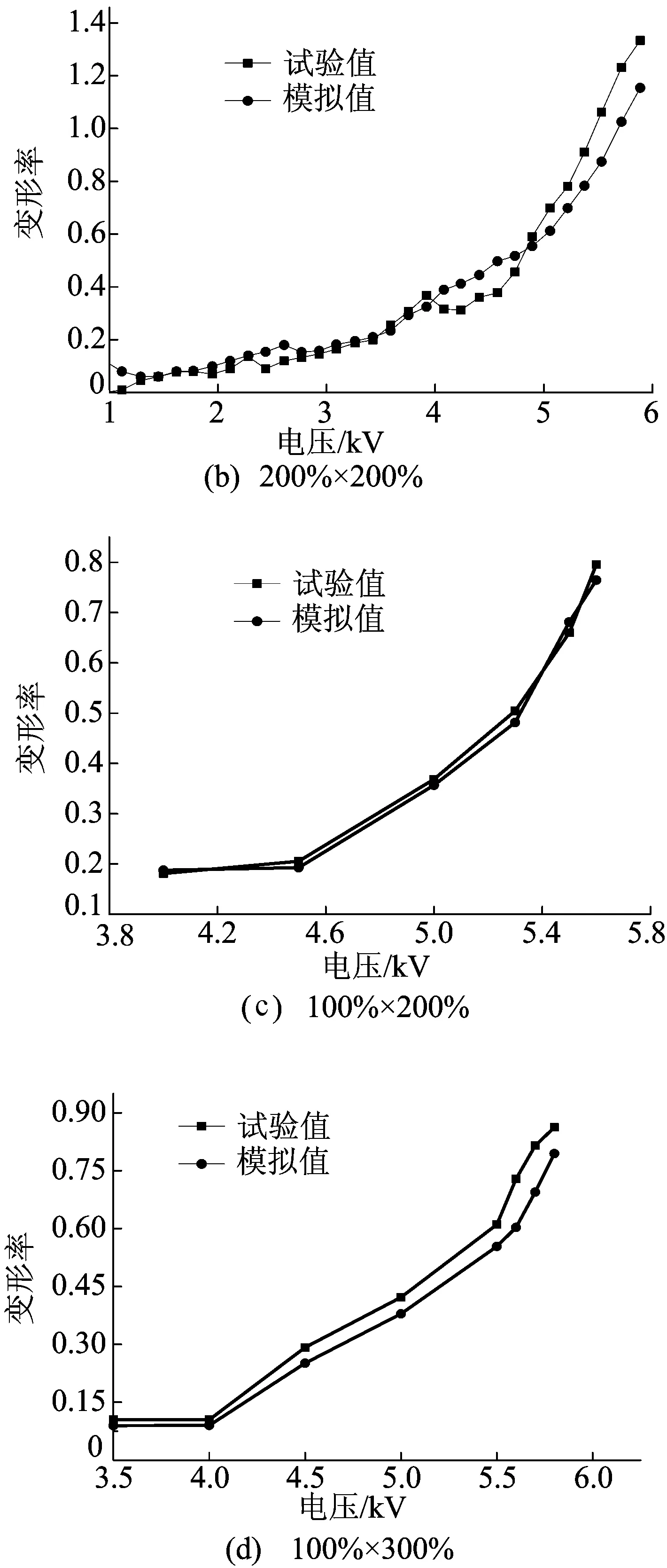
图7 不同预拉伸时模拟值与试验值的比较
4.2机电耦合特性对应变的影响
为了提高DE机电耦合系统的稳定性,面积应变越大,厚度应变就越大,面积应变-电场强度模拟值与试验值如图8所示。

图8 面积应变-电场强度的模拟值与试验值
由图8可知,随着面积增大,电场愈加增强,机电稳定性越高,薄膜材料面积应变的仿真结果小于试验结果,这是由于材料参数以及电致伸缩系数的影响,但是电场随着面积增大而增大的趋势和试验结果基本吻合。这些结果说明机电稳定性行为对器件设计起决定作用。
4.3电极厚度对应变的影响
电极的柔韧性要和薄膜材料一致才能达到与薄膜同步伸缩变形,而且电极材料涂抹的均匀度和厚度对材料变形有很大的影响。不同电极厚度下应变数值分析与试验值的对比如图9所示。

图9 不同电极厚度时模拟值与试验值的比较
仿真试验对比分析表明,不同电极涂抹厚度以及不同种类的电极材料对施加载荷的有效性有影响,电极材料的黏性造成阻力阻碍变形。本试验采用含有碳元素的导电膏,为黑色膏状,材质较软,导电性能非常好。在有限元建模中,电极区域设定为φ19 mm,电极厚度分别取0.45 mm和1 mm,因此在建模时,厚度方向采用多层(5~10层)网格。从图9可以看出,电极厚度为0.45 mm的仿真结果要比1 mm的吻合性好。
5 结 论
本文通过有限元仿真分析方法,选取最适用的Ogden模型材料参数作为模型参数,通过对模型其他参数和边界的设定,构建出DE变形机理有限元模型,模拟了各种试验方案,并通过仿真实验对比验证了材料变形机理特性的影响因素,即预拉伸、电极厚度以及机电耦合特性对DE应变的影响,有限元仿真分析方法为DE变形机理特性研究提供了一种可行的创新方法。
[1]CARPI F,MIGLIORE A,DE ROSSI D.A new contractile linear actuator made of dielectric elastomers[C]//Smart Structures and Materials 2005:Electroactive Polymer Actuators and Devices.SPIE,2005,5759:64-74.
[2]杨宏亮,樊亚玲.管状介电弹性体驱动器电致应变特性分析[J].功能材料与器件学报,2014,20(6):215-218.
[3]PELRINE R,KOHRNBLUH R,PEI Q B,et al.High-speed electrically actuated elastomers with strain greater than 100%[J].Science,2000,287(5454):836-839.
[4]PELRINE R E,KORNBLUH R D,JOSEPH J P.Electrostriction of polymer dielectrics with compliant electrodes as a means of actuation[J].Sensors and Actuators A Physical,1998,64(1):77-85.
[5]曲磊,王建国,钱峰.磁电弹性耦合材料中的本构关系[J].合肥工业大学学报(自然科学版),2012,35(1):78-81.
[6]KOH S J A,LI T F,ZHOU J X,et al.Mechanisms of large actuation strain in dielectric elastomers[J].Journal of Polymer Science Part B:Polymer Physics,2011,49(7):504-515.
[7]李博,朱才子,陈花玲,等.一种离子聚合物金属复合材料的性能研究[J].传感器世界,2008,14(9):14-18.
[8]居刚.基于B样条小波变换的医学影像边缘提取[D].合肥:合肥工业大学,2006.
[9]FAN F,SZPUNAR J A.Characterization of viscoelasticity and self-healing ability of VHB 4910[J].Macromolecular Materials and Engineering,2015,300(1):99-106.
[10]刘立武,孙寿华,刘彦菊,等.具有线性介电常数的Ogden型介电弹性体的本构关系和机电稳定性[J].固体力学学报,2010,31(2):181-192.
[11]谭锋,杨庆山,张建.薄膜结构褶皱分析的有限元法[J].工程力学,2006,23(增刊1):62-68.
[12]李作为,杨庆山,刘瑞霞.薄膜结构褶皱研究述评[J].中国安全科学学报,2004,14(7):16-20.
[13]谭锋,杨庆山,李作为.薄膜结构分析中的褶皱判别准则及其分析方法[J].北京交通大学学报,2006,30(1):35-39.
[14]SAHU R,PATRA K,SZPUNAR J.Experimental study and numerical modelling of creep and stress relaxation of dielectric elastomers[J].Strain,2014,51(1):43-54.
[15]LIU L W,LI J R,LIU Y J,et al.Electric field induced variation of temperature and entropy in dielectric elastomers[J].Journal of Mechanical Science and Technology,2015,29(1):109-114.
(责任编辑胡亚敏)
Finite element analysis of deformation features of dielectric elastomer
CHEN Juan, LIU Kun
(School of Machinery and Automobile Engineering, Hefei University of Technology, Hefei 230009, China)
Dielectric elastomer(DE) is a kind of high molecular polymer thin film materials, which has hyperelastic deformation in electric field and nonlinear characteristic. In this paper, by using the finite element software of ANSYS, selecting suitable Ogden material parameters, and setting suitable parameters of the model and boundary, the finite element model of the deformation mechanism of DE is established. By comparing the finite element simulation results with the experimental data, the deformation mechanism of DE materials is verified, and the influence of the change of drive voltage, magnitude of prestretching and electrode material on the DE deformation mechanism is also studied. The finite element simulation method can be an innovative approach for researching deformation characteristic of DE.
dielectric elastomer(DE); ANSYS software; deformation feature; Ogden model
2015-03-20;
2015-04-14
国家教育部博士点基金资助项目(201200111110026)
陈娟(1970-),女,安徽马鞍山人,合肥工业大学博士生;
刘焜(1963-),男,安徽合肥人,博士,合肥工业大学教授,博士生导师.
10.3969/j.issn.1003-5060.2016.07.003
TQ334
A
1003-5060(2016)07-0875-06
