一类非线性振动方程的定性分析

李　鹏，窦霁虹，仲文林，卢克英

(西北大学 数学学院, 陕西 西安　710127)



·数理科学·

一类非线性振动方程的定性分析

李鹏，窦霁虹，仲文林，卢克英

(西北大学 数学学院, 陕西 西安710127)

对一类非线性振动方程进行定性分析与探究,并推广了此类方程。采用行列式-迹法则、小参数扰动、首次积分和Bendixson-Dulac判别法。证明了方程对任何参数都不存在闭轨线和奇异闭轨线,分析了方程在特殊情形下奇点个数、类型。丰富了已知结果, 使其适用范围更广。

振动方程; 定性分析; 闭轨线; 极限环;Dulac判别法

文献[1]给出了一类由微分方程

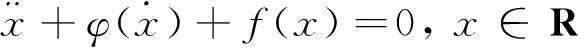
(1)

(2)

在mb≠0时,对任何参数都不存在闭轨线和奇异闭轨线。文献[2]中未分析式(2)平衡点的类型及其稳定性;也未考虑b=0时,系统极限环的存在性。本文首先在方程(2)的基础上推广并得到一类特殊振动方程满足适当条件后,仍然具有文献[2]的结论；其次，针对文献[2]中的不足进行补充。这一探究更加丰富振动方程理论，对于物理学中机械振荡和周期振荡的研究具有深刻意义。

引理1[3]设G为单连通域,若存在一次可微函数B1(x,y)与F(x,y),使

在G中保持常号,且不在任何子区域中恒等于零,则方程不存在全部位于G中的闭轨线和奇异闭轨线。

引理2[2](Bendixson-Dulac判别法)若在单连通域G内存在函数B(x,y)∈C1(G),使

且不在G的任何子区域内恒为零,则系统不存在全部位于G内的闭轨线和具有有限个奇点的奇异闭轨线。函数B(x,y)称为Dulac函数。

引理3[2]设有系统

其中X和Y在O(0,0)邻域内解析,O(0,0)为其对应线性系统的中心点,若在O(0,0)邻域S(0,δ)内存在此系统的一个连续的首次积分,则O(0,0)必为中心。

本文主要研究一类非线性振动方程

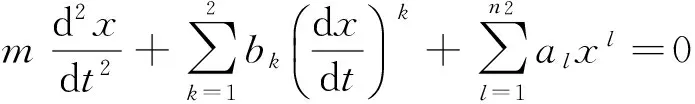
(3)

1　主要定理

定理1若mb1≠0,则方程(3)对于任何参数都不存在闭轨线和具有有限个奇点的奇异闭轨线。

证 明假设振动方程式(3)的更一般形式

(4)

(5)

取E(x,y)≡C1, 其中C1为常数,则

(6)

只有选取F(x,y)≡C2x,其中C2为常数。

对于x,y∈R,要使得式(6)符号确定,则有如下结论:当k=1或2,l=1,2,3，…时,式(6)可以化为

(7)

将非线性殊振动方程式(3)进一步推广为

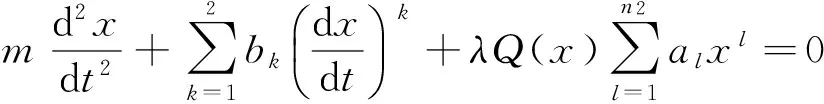
(8)

其中Q(x)是一类关于变量x的非多项式[4-7],并满足:

1)Q(x)是连续函数,在x=0处具有n阶导数;

2)Q(x)在x=0处取值为0,即Q(0)=0;

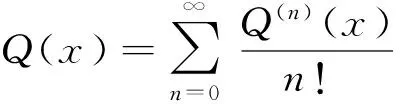
使之也具有对于任何参数都不存在闭轨线和奇异闭轨线,得到如下定理。

定理2若λ≠0，mb1≠0,则振动方程式(8)对于任何参数都不存在闭轨线和具有有限个奇点的奇异闭轨线。

证 明仿照定理1的证明,取E(x,y)≡C3,取F(x,y)≡C4x,其中C3,C4为常数,同样可得如下结果:

关于定理2,给出2个典型振动方程作为实例通过Matlab软件对振动方程进行数值模拟[9]。

例1振动方程

(9)

当mb1≠0时，对于任何参数都不存在闭轨线和具有有限个奇点的奇异闭轨线。取m=1.0,b1=-0.3,b2=-0.8,λ=0.4,a1=0.1,a2=0.3,a3=0.4,其余参数为0,轨线图如图1所示。

图1　振动方程式(9)的轨线图Fig.1　Trajectory of vibration equation (9)

取m=1.0,b1=0.3,b2=-0.8,λ=0.4,a1=0.1,a2=0.3,a3=0.4,其余参数为0,轨线图如图2所示。

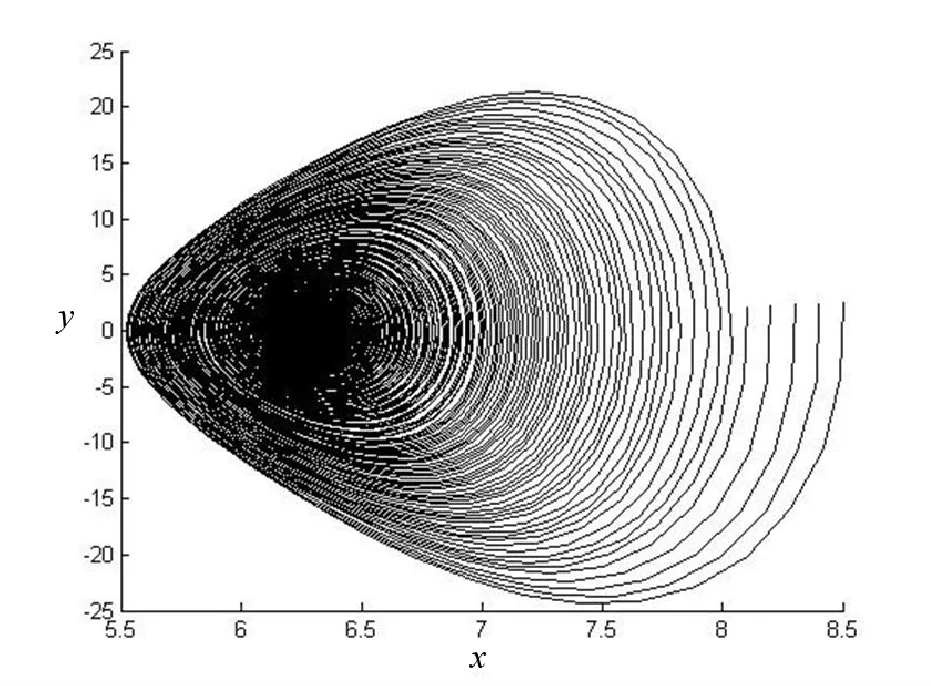
图2　振动方程式(9)的轨线图Fig.2　Trajectory of vibration equation (9)

结果分析：只改变b1符号，其他参数值不变时，方程式(9)轨线图发生改变，但是不存在极限环或奇异闭轨线。

例2振动方程

(10)

当mb1≠0时，对于任何参数都不存在闭轨线和具有有限个奇点的奇异闭轨线。取m=1.0,b1=-0.3,b2=-0.8,λ=0.3,a1=0.1,a2=0.3,a3=0.4,其余参数为0,轨线图如图3所示。

图3　振动方程式(10)的轨线图Fig.3　Trajectory of vibration equation (10)

取m=1.0,b1=0.3,b2=-0.8,λ=0.3,a1=0.1,a2=0.3,a3=0.4,其余参数为0,轨线图如图4所示。

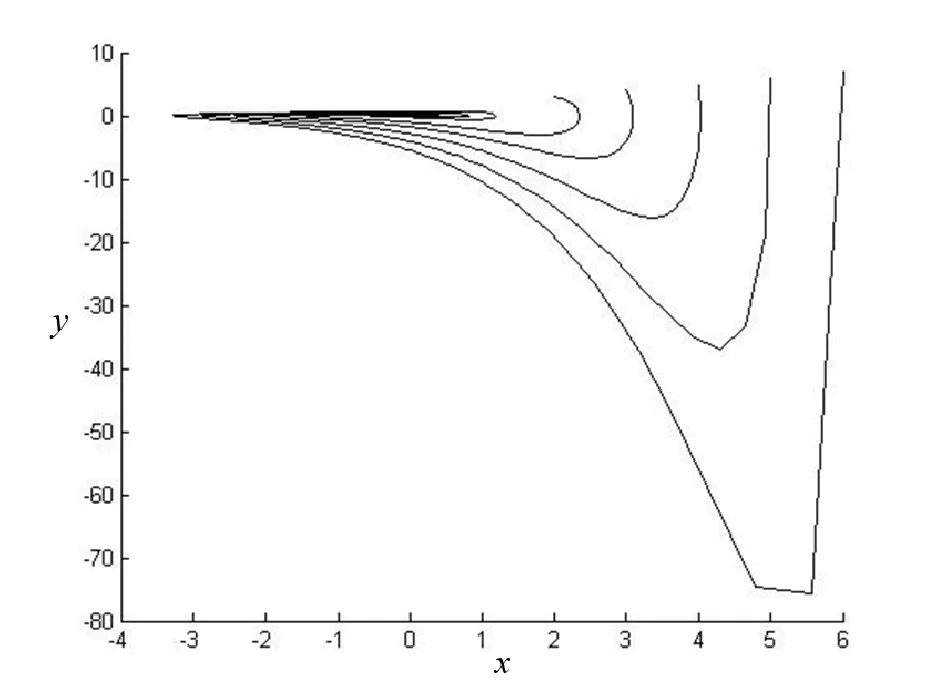
图4　振动方程(10)式的轨线图Fig.4　Trajectorg for ribration equation (10)

结果分析:只改变b1符号，其他参数值不变时，方程式(10)轨线图发生改变，但是不存在极限环或奇异闭轨线。

综上，由例1和例2中的振动方程式(9)，(10)的轨线图验证定理2结论成立。

本文还研究振动方程式(3)特殊情形下的方程:

(11)

(12)

由定理1可知方程式(11)不存在极限环由于在上述振动方程中m代表质量,故本文只考虑参数m>0时,系统(12)平衡点性态和极限环的存在性。

2　定性分析

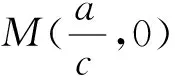
(13)

记p=-tr(D),q=det(D)。

(i)当c=0时,系统只有唯一奇点O(0,0),将其代入式(13)得

当a<0时,有q<0,故奇点O(0,0)为不稳定鞍点;

当a>0,b>0,b2-4ma>0时,有p>0,q>0,p2-4q>0,故奇点O(0,0)为稳定结点;

当a>0,b<0,b2-4ma>0时,有p<0,q>0,p2-4q>0,故奇点O(0,0)为不稳定结点;

当a>0,b>0,b2-4ma≤0时,有p>0,q>0,p2-4q≤0,故奇点O(0,0)为稳定焦点或稳定临界结点或稳定退化结点;

当a>0,b<0,b2-4ma≤0时,p<0,q>0,p2-4q≤0,故奇点O(0,0)为不稳定焦点;或不稳定临界结点或不稳定退化结点;

当a>0,b=0时,有p=0,q>0,故奇点O(0,0)为中心。

当a=0时,系统(12)有奇线y=0。有关奇线的性态在这里不予分析。

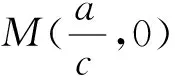
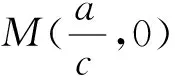
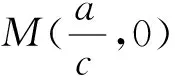
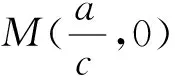
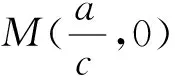
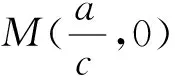
当a=0,c≠0时,有q=0,故奇点O(0,0)是高阶奇点,采用小参数扰动法[2]来分析高阶奇点的类型。

引入参数ε,0<ε≪1,考查辅助系统

(14)

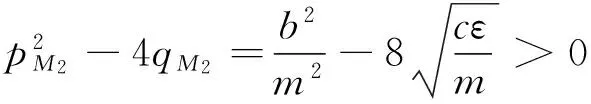
经判断后可得M1是鞍点;M2为稳定结点。当ε无限靠近时M1和M2均向O点逼近。当ε→0时式(14)就变为

(15)

此时M1和M2在O点重合,从而形成鞍结点。

定理4当b≠0时,对于系统式(12)中任何参数都不存在闭轨线和奇异闭轨线;当b=0时,系统式(12)必存在闭轨线。

(16)

取Duluc函数B(x,y)=e-2Dx，且当B≠0时，即b≠0时，有

恒成立,故由引理2可知当b≠0时,对于任何参数,系统式(12)都不存在闭轨线和奇异闭轨线。

当B=0,即b=0时,系统(16)是可积的,存在连续的首次积分。

(i)当D=0且B=0时,存在连续的首次积分

其中c0为任意常数。

(ii)当D≠0，B=0时,也存在连续首次积分。

首先将方程式(16)化为:

(Ax-Cx2-Dy2)dx+ydy=0

(17)

记M(x,y)=Ax-Cx2-Dy2,N(x,y)=y。

由文献[10]，利用积分因子，将式(9)转化为恰当微分方程后，可以采用通积分求出式(8)或式(9)的通解。经计算:

故式(17)的一个积分因

μ(x,y)=e∫-2Ddx=e-2Dx，

则式(17)转化为一个恰当方程:

μ(x,y)M(x,y)dx+μ(x,y)N(x,y)dy=0。

(18)

对于恰当方程(18)可求得通积分u(x,y)=c,它同时满足

(19)

(20)

对式(19)关于x积分得到

(21)

将u(x,y)代入式(20)可得

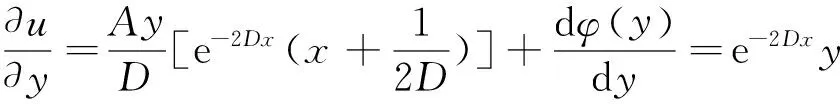
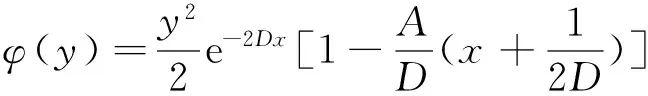
并代入式(21)，可得

所以方程(17)的通解为

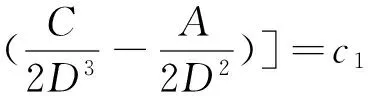
其中c1为任意常数。故方程式(17)的一个连续首次积分为

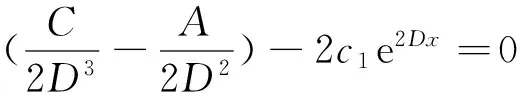
根据定理3可得:当B=0时,即b=0时,O(0,0)为其对应线性系统的中心点。结合引理3可得:当b=0时,O(0,0)必为中心,故系统必存在闭轨线。定理3和4的结论对文献[2]作了进一步补充。

3　结　论

由于奇点附近轨线分布的复杂性,对其研究是定性分析的重要部分,此外它反映了客观世界中重要的静止平衡状态,有着重要的应用价值[11-13];其次闭轨线,奇异闭轨线和极限环在研究定性结构中扮演着重要角色，反映了现实世界中大量存在的周期振荡现象。

[1]陆启韵.常微分方程的定性方法和分叉[M].北京：北京航空航天大学出版社，1989：207-208.

[2]马知恩,周义仓.常微分方程定性与稳定性方法[M].北京：科学出版社，2015.

[3]叶彦谦.极限环论[M].上海：上海科学技术出版社，1984：14-22.

[4]DUJia,XIAOJian.ExistenceofLimitCyclesforaclassof(n+1)-thPolynomicalsystem[J].ChineseJournalOfEngineeringMathematics，2014,31(2)：274-285.

[5]DUJia,XIAOJian.Limitcycleandbifurcationproblemforaclassofnonpolynomialplanardifferentialsystems[J].CommunicationonAppliedMathematicsandComputation, 2014,128(2)：189-198.

[6]朱勇,姜万录.摩擦力作用下电液伺服系统非线性动力学行为[J].北京航空航天大学学报，2015，1：41-01.

[7]李国涛,刘兴国.一类非多项式微分系统的定性分析[J].湖南工业大学学报，2008，122(6)：10-12.

[8]韩彦伟,曹庆洁.一类几何非线性系统的动力学行为及应用研究[D]. 哈尔滨：哈尔滨工业大学，2015：10.

[9]薛定宇,陈阳泉.高等应用数学Matlab求解[M].3版.北京：清华大学出版社，2013：10.

[10] 王高雄,周之铭.常微分方程[M].3版.北京：高等教育出版社，2010：55.

[11] 惠俊鹏,杨超.考虑参数摄动的飞行器气动伺服弹性鲁棒稳定性分析研[J].导弹与航天运载技术，2015,8：1-5.

[12] 罗海洋.受电磁激励连续转子系统非线性振动与稳定性[D].大连：大连理工大学，2014.

[13] 张国策.陈立群磁场中悬臂梁的非线性振动[D].上海：上海大学，2014.

(编辑亢小玉)

The qualitative analysis of a type of Nonlinear vibration equation

LI Peng, DOU Ji-hong, ZHONG Wen-lin, LU Ke-ying

(School of Mathematics, Northwest University, Xi′an 710127， China)

To do qualitative analysis of and exploration for a special type of vibration equation, at last the promotion and extension of the equation were done.The determinant of trace rule, small parameter perturbation, the first integral and Bendixson-Dulac discriminant are applied into the analysis on the vibration equation for qualitative analysis. Under different parameters, the number and type of singularities was proved.In the sequel, to prove that the equation for any parameters doesn′t exist closed trajectories and the singular closed trajectories. The obtained results improve and expand the related known works.

vibration equation; qualitative analysis; closed trajectories; limit cycle; Dulac discriminant method

2015-04-03

西北大学研究生自主创新基金资助项目(YZZ14083)；陕西省教育厅自然科学专项基金资助项目(CU063120603000)

李鹏，男，山西忻州人，从事微分方程定性与稳定性研究。

窦霁虹，女，陕西西安人，教授，从事微分方程定性理论研究。

O175.12

A

10.16152/j.cnki.xdxbzr.2016-04-001