粒化的Mean Shift行人跟踪算法

刘翠君，赵才荣，苗夺谦，王学宽

(同济大学 电子与信息工程学院，上海 201804)



粒化的Mean Shift行人跟踪算法

刘翠君，赵才荣，苗夺谦，王学宽

(同济大学 电子与信息工程学院，上海 201804)

Mean Shift行人跟踪采用颜色特征直方图作为跟踪特征，存在易受背景颜色干扰等问题。基于此，在传统的Mean Shift行人跟踪算法中引入粒计算的思想，提出粒化的Mean Shift行人跟踪算法，对图像目标区域作粒层分块来提取块颜色特征信息，并在颜色特征表示上作不同粒度的粒化，最后在Mean Shift迭代框架下实现行人跟踪。该方法相比传统的跟踪方法具有计算复杂度更低、稳健性更好的优点。在PETS2009和CAVIAR数据库上的实验表明，这种方法跟踪正确率更高，在颜色干扰下稳健性更好，能够实时有效地跟踪行人。

信息粒；粒计算；Mean Shift；特征提取；行人跟踪

中文引用格式：刘翠君，赵才荣，苗夺谦，等. 粒化的Mean Shift行人跟踪算法[J]. 智能系统学报， 2016, 11(4): 433-441.

英文引用格式：LIU Cuijun， ZHAO Cairong， MIAO Duoqian， et al. Granular mean shift pedestrian tracking algorithm[J]. CAAI Transactions on Intelligent Systems, 2016, 11(4): 433-441.

行人跟踪涉及行人检测和行人跟踪两部分。行人检测属于运动目标检测，目的是从图像序列中将行人目标从背景图像中提取出来；行人跟踪则是在视频图像序列中检测定位出行人，包括目标建模、目标匹配和目标定位[1]。行人跟踪算法分属两大类：确定性跟踪和随机跟踪。确定性跟踪以Mean Shift (MS)跟踪为主线，是以相似度度量作为代价函数的优化问题，有一系列基于MS的跟踪算法[2-9]；随机跟踪将视觉跟踪转化为贝叶斯理论框架下的状态估计问题，目前典型的随机跟踪算法有Kalman滤波跟踪[10]和粒子滤波跟踪[11]。以MS为代表的行人跟踪算法因其简单稳健的优势而广受研究者青睐。文献[1]对MS跟踪算法的经典文献和研究历程做了详细综述。2003年D.Comaniciu 等[2]将MS应用于视觉跟踪领域，首次提出MS跟踪算法，开辟了视觉跟踪领域的新方向，自此有大量关于MS的改进算法被提出。为提高MS跟踪算法的适应能力，在目标模板更新策略上，文献[3]提出基于线性加权的模板更新；文献[4]提出基于滤波的模板更新方法；在目标尺度及方向估计上，文献[5]提出基于特征点匹配的尺度与方向估计方法，消除由于尺度变化导致的定位误差；文献[6]提出基于权重图的尺度与方向估计方法，能更准确地反应目标尺度信息；在抗遮挡跟踪上，文献[7]在MS跟踪算法的基础上引入Kalman滤波器来辅助预测目标位置，增强了稳健性；文献[8]提出目标分块的方法，通过子块的跟踪定位来获得目标的整体位置；在跟踪快速目标上，MS迭代容易陷入局部最优值，使得无法处理快速运动的目标，文献[9]引入模拟退火算法，提出退火MS来逐步平滑代价函数，用于全局模式的搜索，跳出局部最优值。

MS跟踪向来以计算简单、调节参数少为优势，这些改进算法尽管从不同方面改进了MS跟踪算法的缺陷，但是也一定程度上增加了计算复杂度和调节参数，无法很好地保证跟踪实时性。 MS跟踪存在的挑战问题有许多，本文旨在基本保留MS的跟踪框架上解决MS跟踪的基本问题：颜色直方图带来的干扰问题和计算复杂度问题。考虑到颜色直方图对于目标形状、姿态、旋转等变化及遮挡都具有一定的鲁棒性，但是由于摄像机的视频图像质量普遍较差，分辨率普遍较低，易受背景颜色干扰，使得采集到的目标颜色特征存在较大的噪声冗余信息，然而粒计算方法恰巧能有效地处理视频图像大数据冗余信息。

粒计算方法由Zadeh[12]和Lin[13]首次提出，是人工智能领域中的一种新理念和新方法，它覆盖了所有和粒度相关的理论、方法和技术，主要用于对不确定、不精确、不完整信息的处理，对大规模海量数据的挖掘和对复杂问题的求解[14]。粒计算的实质是通过选择合适的粒度，来寻找一种较好的、近似的解决方案，避免复杂的计算，从而降低问题求解的难度。文献[15]归纳了粒计算方法在大数据处理中的3种基本模式并讨论了粒计算方法应用于大数据的可行性及优势。考虑到摄像机视频图像中的海量数据挖掘和行人跟踪问题的复杂计算，试图通过粒计算方法找到降低计算代价并有效改进跟踪效果的方法。

本文提出粒化的MS行人跟踪算法，基本保留MS跟踪算法框架，引入粒计算方法来优化颜色特征表示，在颜色特征的采集和处理上都采用粒计算方法表示，得到粒化后的核函数加权颜色直方图作为颜色特征表示，通过MS迭代实现行人跟踪，一定程度上削弱了图像噪声干扰，不仅降低了计算代价，而且提高了跟踪实时性。

1　颜色特征粒化

将大量的复杂特征及信息按其各自的特征及性能划分为若干个较简单的块，每一块看作是一个信息粒，这些信息粒具有相似的特征及性能，这个划分过程就是信息粒化的过程。

定义1用一个三元组来描述信息粒G=(IG,EG,FG)，其中IG称为信息粒G的内涵，EG称为信息粒G的外延；FG称为内涵和外延之间的转换函数。

信息粒的内涵IG是信息粒在特定环境下的表现知识，表示在一个特定的任务下信息粒中所有元素的一般性特征、规则、共同性等，可以定义一个语言，由这个语言的公式来表示；信息粒的外延EG是满足这个公式的所有对象的集合；信息粒的转换函数FG是EG到IG的泛化转换函数。对于信息粒G=(IG,EG,FG)，X为对于信息粒G所有可能外延EG的对象的集合，即外延的论域；Y为对于信息粒G所有可能内涵IG的集合，即内涵的论域。下面给出转换函数FG的形式化定义。

定义2从X到Y的信息粒的泛化转换函数是笛卡尔积X×Y的一个子集FG，对于每个属于X的EG都存在唯一的Y中的元素IG使得(EG,IG)属于FG。

传统的MS行人跟踪算法采集行人目标区域的颜色特征信息，粒化的MS行人跟踪算法引入粒计算的思想对颜色特征信息进行粒化，包含两个信息粒化过程：图像粒化和颜色通道粒化。

1.1图像粒化

行人目标区域存在背景颜色干扰，为了减弱背景颜色干扰和降低计算代价，将图像行人目标区域进行不同粒度的粒层分块，并采集每一粒块的R、G、B颜色均值，得到图像特征信息粒格，简称图像粒，该过程为图像粒化。用三元组GI=(IGI,EGI,FGI)表示图像粒，内涵IGI是由外延EGI集合中的每个对象通过转换关系FGI计算出的R、G、B颜色均值集合。外延EGI的论域XI={M×NM,N∈}，其中M×N表示大小为M×N的图像粒块，∈XI,i=1,2,…,nRI，表示图像粒度为RI时的第i个图像粒块，其中RI={1,2,…}表示图像粒层分块的粒度。相同粒度下的图像粒块大小一致，令原始图像块大小为m×n，图像粒度为RI时的图像粒块的大小为mRI×nRI，nRI表示粒度为RI时的图像粒块总数，有

(1)

(2)

转换函数对外延集合中的每个图像粒块求R、G、B三通道的颜色特征均值，得到图像粒的内涵集合，外延集合中的粒块对象和内涵集合中颜色特征向量对象一一对应，内涵集合中的所有颜色特征向量对象构成该图像目标区域的颜色特征矩阵。

图1为粒化的MS行人跟踪算法的图像粒化过程示意图。

图1　图像粒化过程Fig.1　Image granulation

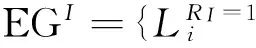
1.2颜色通道粒化

行人跟踪的视频图像往往分辨率较低，存在一定程度的颜色噪声干扰。颜色级数越多，表示的颜色信息就越多，但是相应的颜色干扰信息也越多，且运算代价也越大，通过颜色特征计算相似性度量参数(巴氏系数)的速度也越慢，这对行人跟踪需要高实时性的要求具有很大挑战，因此不利于实时的行人跟踪。粒计算的思想能有效地对这种不确定的模糊信息进行简化处理，因此在颜色特征表示上引入粒计算的思想：行人目标区域经过图像粒化和转换函数处理后得到行人目标区域的颜色特征矩阵，对颜色特征矩阵做颜色通道粒化处理得到最终粒化后的颜色特征矩阵。

分别将R、G、B三通道颜色区间进行不同粒度的量化，每通道的颜色区间都均匀二分，得到一系列均匀的子颜色区间，称为颜色区间信息粒格，简称颜色粒，该过程为颜色通道粒化。用三元组GC=(IGC,EGC,FGC)来表示颜色粒，内涵IGC是由外延EGC集合中的每个颜色区间通过转换关系FGC计算出的R、G、B颜色量值集合。外延EGC的论域为XC={[a,b],0≤a,b≤255,a,b∈}，∈XC,i=1,2,…,nRC表示颜色粒度为RC时第i个颜色粒区间，nRC=2RC-1表示颜色粒度为RC时的颜色粒总数，则颜色粒度为RC时的每一个颜色粒区间长度为

(3)

(4)

(5)

至此可直接通过转换函数式(5)计算出颜色特征值在任一粒度下粒化后的颜色特征值，较大程度降低计算量。

计算经过颜色通道粒化后的3个颜色通道的直方图虽然已经降低了一定的计算代价和存储代价，但是为了更进一步简化计算量和降低存储代价，将颜色粒化后的三通道颜色值整合成一维颜色值作为该颜色粒的颜色特征值，由于颜色的权重信息已经在颜色粒化的时候通过颜色粒度表现，因此整体的转换函数f(v)直接体现为各颜色通道的转换函数的叠加，且保证f(v)≥1，表达为

(6)

未经颜色特征粒化(a)和经过颜色特征粒化后的颜色直方图(b)如图2所示。

(a)颜色特征直方图

(b)粒化的颜色特征直方图图2　颜色直方图Fig.2　Color histogram

比较两图，可看到粒化后的颜色直方图在颜色级数上降低了大约5倍，曲线与横轴所围成的面积是采集的目标区域的像素点数量，可见粒化后的像素点数量大约降低了4倍，大大降低了计算量。这一点将在后续的实验中得到进一步的验证。

2　粒化的Mean Shift行人跟踪算法

粒化的Mean Shift行人跟踪算法(GMS)是利用图像粒化及颜色通道粒化后的核函数空间加权的颜色直方图作为目标模型，采用巴氏系数作为相似度度量，通过自适应步长的MS迭代来实时跟踪行人目标的位置。

2.1算法描述

(7)

(8)

(9)

(10)

同理，设在跟踪过程中行人目标候选区域的颜色直方图经过图像粒化和颜色通道粒化后表示为p(y0)={pu(y0)}u=1,2,…,mRC，其中y0为目标候选区域的中心位置，同样有

(11)

基于巴氏系数，求得目标区域的参考颜色直方图q和目标候选区域的颜色直方图p(y0)的相似度为

(12)

至此，粒化的MS行人跟踪算法的MS跟踪迭代步骤可以总结为算法1。

算法1粒化的Mean Shift行人跟踪算法(GMS)

输入行人跟踪视频图像序列。

跟踪过程

3)计算行人目标新位置y1：

4)计算新位置的颜色直方图{pu(y1)}u=1,2,…,mRC。

7)若‖y1-y0‖<ε，则本轮迭代结束；否则y0←y1返回1)继续迭代更新行人目标位置。

输出当前帧行人目标区域实时最优位置。

2.2算法计算复杂度

表1　MS和GMS的运算代价

表中Cw、Cp、Cm、Ca、Cr、Cd、Cs分别表示核函数加权、获取像素值、浮点数乘法、加法、移位运算、除法运算和开方的计算代价；R、u分别表示MS算法中的行人目标区域大小及颜色直方图的级数；R′、u′分别表示GMS算法中的行人目标区域大小及颜色直方图的级数；满足近似关系R/R′=4，u/u′≈5，Cm和Cr的关系无法准确比较，但是Cm≻Cr一定成立。至此可近似估计出MS和GMS的每次迭代的计算代价关系，为式(13)。理论计算得出，仅考虑各运算代价时，GMS算法比MS算法的计算代价至少快4倍，是个可观的结果。在实际实验中，由于图像分块函数消耗、硬件等原因会使得真正计算效率低于4倍。

(13)

3　实验结果与分析

在CPU2.6 GHz、内存4 GB的PC机、MATLAB (R2013b)的环境下进行实验，实现本文的改进算法GMS跟踪算法，并实现传统MS跟踪算法、Kalman滤波跟踪算法和粒子滤波跟踪算法与之比较。

采用4组视频图像序列进行实验，图像序列选自PETS2009和CAVIAR视频图像库，涵盖了行人跟踪的主要场景及挑战场景，包括简单背景、复杂背景、目标遮挡、形变及光照变化等。为检测本文方法的性能，将与传统MS跟踪算法、Kalman滤波跟踪算法和粒子滤波跟踪算法进行比较分析。

3.1与传统MS跟踪的比较

图3选取的视频图像是S2_L1项目中View_005中的部分序列，序列中红衣女子从视频窗口右端水平穿过走向视频窗口左端，期间活动窗口只有红衣女子一人，跟踪图像背景较简单。其中图3(a)是MS的跟踪结果，图3(b)是GMS的跟踪结果。从跟踪结果可发现该序列MS和GMS的跟踪效果都较好，在整个行人跟踪过程中都有正确跟踪到目标行人，但是观察表2发现该序列MS算法的平均迭代次数接近5，而GMS算法的平均迭代次数3.5左右，跟踪实时性提高了30%。可见在跟踪背景比较简单，行人目标颜色特征较为明显时，虽然MS算法和GMS算法的跟踪准确率相差无几，但是GMS算法由于引入了粒计算，降低了计算复杂度，因此一定程度上提高了跟踪实时性。

(a)MS跟踪结果

(b)GMS跟踪结果图3　Image I 跟踪结果比较Fig.3　Comparison of tracking results of image I

图4选取的视频图像是S2_L1项目中View_005中的部分序列，序列中蓝衣女子从视频窗口右端水平穿过走向视频窗口左端，走到视频窗口中央时与两名黑衣男子发生遮挡随后分离。由于有行人遮挡及背景颜色干扰，跟踪图像背景略复杂。其中图4(a)是MS的跟踪结果，图4(b)是GMS的跟踪结果。比较图4的跟踪结果，发现目标行人未发生碰撞前，MS和GMS都有正确跟踪到行人，在第144帧目标行人与两个行人发生碰撞后(即遮挡后分离)，在第147帧及第148帧MS目标跟踪丢失，发现跟踪到干扰行人的蓝色牛仔裤上，与目标行人的颜色特征相似度较高，导致误判，直至最后目标彻底丢失。而在整个行人跟踪过程中，GMS跟踪目标未丢失，跟踪正确率较高，仅在第144帧行人发生遮挡时跟踪略有偏差，遮挡分离后，跟踪回复正常。可见当跟踪场景中存在与行人目标的颜色特征相似的候选目标与行人目标碰撞时，MS算法跟踪失效，GMS算法的粒化后颜色直方图一定程度上降低了背景颜色特征的干扰，使得跟踪正确保持。该序列MS的平均迭代次数接近6，GMS的平均迭代次数约为4.5，跟踪实时性提高了25%，但是相比序列一的GMS平均迭代次数，每帧图片平均增加了一次迭代，这是因为Image II跟踪场景相比Image I更为复杂。

(a)MS跟踪结果

(b)GMS跟踪结果图4　Image II 跟踪结果比较Fig.4　Comparison of tracking results of image II

图5选取的视频图像是S2_L1项目中View_001中的部分序列，序列中红衣女子从视频窗口右下端斜向上走向视频窗口左上端，走到视频窗口中央时与两名黑衣男子发生遮挡随后分离，紧接着又被电线杆遮挡后又分离。跟踪图像背景略复杂，发生多次遮挡，包括两行人的动态遮挡和电线杆的静态遮挡，而且背景局部区域存在光照变化干扰。其中图5(a)是MS的跟踪结果，图5(b)是GCMS的跟踪结果。MS跟踪在第467帧时，行人跟踪丢失，跟踪结束；GMS在第467帧时，行人跟踪略有偏差，但是仍继续正确跟踪。整个跟踪过程中，行人目标的颜色特征与背景颜色特征和遮挡物体的颜色特征能很好地区分，GMS在目标行人发生遮挡时，能适当减弱背景及遮挡物体的颜色干扰，跟踪效果很好，而MS算法更多地受背景及遮挡物体的颜色干扰导致多次遮挡之后行人彻底丢失。该序列MS的平均迭代次数约为5.5，GMS的平均迭代次数约为4.5，跟踪实时性仅提高了18%，可见GMS算法在跟踪场景复杂的情况下，跟踪效果还有待提升。

(a)MS跟踪结果

(b)GMS跟踪结果图5　Image III 跟踪结果比较Fig.5　Comparison of tracking results of image III

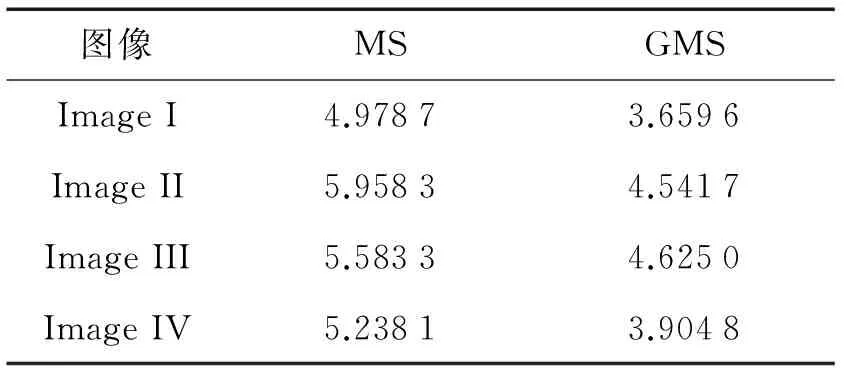
表2　MS和GMS的平均迭代次数(次/帧)

(a)MS跟踪结果

(b)GMS跟踪结果图6　Image IV跟踪结果比较Fig.6　Comparison of tracking results of image IV

图6选取的视频图像是CAVIAR数据库FRONT VIEW中的部分序列，序列中目标行人从视频窗口右端水平穿过走向视频窗口左端，走过视频窗口中央时与多名行人发生遮挡随后分离。整个视频图像质量较差，行人特征极其不明显，光照变化很大，加之有行人遮挡及背景颜色干扰，跟踪图像背景更为复杂。其中图6(a)是MS的跟踪结果，图6(b)是GMS的跟踪结果。观察(a)、(b)的跟踪结果，在第493帧发现MS目标跟踪片刻丢失，GMS目标跟踪仅仅略有偏差，这是因为MS需要获取更多的颜色信息，相对应的对光照变化会更加敏感；第549、564、573帧捕捉了目标行人碰撞过程，由于行人特征实在不明显使得MS跟踪失效，而GMS能适当地容忍颜色特征干扰，使得碰撞过程行人跟踪正常。可见当跟踪视频质量较差时GMS比MS更具有优势。

3.2与其他类跟踪方法的比较

观察Image I红衣女子的跟踪结果(图7)，发现针对简单背景的行人跟踪，Kalman滤波和粒子滤波总体上都能较好地跟踪到目标行人，不会丢失。该序列光照基本无变化，目标行人运动基本匀速，两个算法在第477帧跟踪位置都有偏差，但是随后跟踪正常，这是因为Kalman滤波预测初始参数的原因，随着跟踪状态的变化，参数会随时调整，这是不可避免的；粒子滤波的粒子采样初始是无经验无知识的，粒子覆盖整个跟踪图像，伴随着不断的重采样，粒子会渐渐地集中在行人目标上，跟踪位置也不断精确。

(a)Kalman 滤波跟踪结果

(b)Particle 滤波跟踪结果图7　Image I 跟踪结果比较Fig.7　Comparison of tracking results of image I

观察Image III红衣女子的跟踪结果(图8)，发现复杂背景下且存在行人互遮挡、光照变化等挑战因素时，Kalman滤波和粒子滤波跟踪都失效，行人目标极易丢失，这是因为传统Kalman滤波和粒子滤波跟踪都是利用状态估计来预测行人目标的位置，而光照变化等因素极易干扰粒子采样，可见MS跟踪采取颜色直方图作为跟踪特征具有一定的优势。

(a)Kalman 滤波跟踪结果

(b)Particle 滤波跟踪结果图8　Image III跟踪结果比较Fig.8　Comparison of tracking results of image III

3.3跟踪效率分析

表3展示了不同方法在不同图像序列中的平均跟踪效率(s/帧)，发现GMS的跟踪效率均比MS的跟踪效率高，说明GMS跟踪算法在实际跟踪场景下确实降低了运算代价，提高了跟踪实时性。同时发现相比简单场景下，Kalman滤波和粒子滤波的跟踪效率更胜GMS。观察序列三各方法的跟踪效率发现Kalman滤波和粒子滤波结果很小，这是因为Kalman滤波和粒子滤波跟踪目标已经彻底丢失，所以该序列数据失去参考价值。

表3　不同跟踪方法的平均跟踪效率比较

4　结论

在跟踪场景中若存在与行人目标颜色特征相似的干扰物体时，特别是碰撞时或被遮挡时，传统的MS行人跟踪算法会使得跟踪目标丢失。因此，本文提出了粒化的MS行人跟踪算法，总结如下：

1)采用粒计算的思想对行人目标区域进行粒化分块，并且对分块后的块颜色特征进行颜色通道粒化，归一化后得到粒化后的颜色直方图作为跟踪过程的行人目标颜色特征表示；

2)通过巴氏系数衡量行人目标区域和候选区域的相似度，最后通过MS迭代框架来实时跟踪目标行人的位置；

3)算法保持了传统MS跟踪算法的基本框架，因此也延续了传统MS跟踪算法的优势，且使得算法的计算复杂度更低，跟踪更快；

4)通过实验分析得出，本算法减弱了跟踪场景的背景颜色干扰，同时提高了跟踪实时性。

[1]顾幸方, 茅耀斌, 李秋洁. 基于Mean Shift的视觉目标跟踪算法综述[J]. 计算机科学, 2012, 39(12): 16-24.

GU Xingfang, MAO Yaobin, LI Qiujie. Survey on visual tracking algorithms based on mean shift[J]. Computer science, 2012, 39(12): 16-24.

[2]COMANICIU D, RAMESH V, MEER P. Kernel-based object tracking[J]. IEEE transactions on pattern analysis and machine intelligence, 2003, 25(5): 564-577.

[3]KHAN Z H, GU Yuhua, BACKHOUSE A G. Robust visual object tracking using multi-mode anisotropic mean shift and particle filters[J]. IEEE transactions on circuits and systems for video technology, 2011, 21(1): 74-87.

[4]PENG Ningsong, YANG Jie, LIU Zhi. Mean shift blob tracking with kernel histogram filtering and hypothesis testing[J]. Pattern recognition letters, 2005, 26(5): 605-614.

[5]CHEN Aihua, ZHU Ming, WANG Yanhua, et al. Mean shift tracking combining SIFT[C]//Proceedings of the 9th International Conference on Signal Processing. Beijing: IEEE, 2008: 1532-1535.

[6]NING Jifeng, ZHANG Lei, ZHANG D, et al. Scale and orientation adaptive mean shift tracking[J]. IET computer vision, 2012, 6(1): 52-61.

[7]CHEN Kangli, GE Wancheng. Pedestrian tracking algorithm based on kalman filter and partial mean-shift tracking[C]//Proceedings of the 2nd International Conference on Systems and Informatics. Shanghai: IEEE, 2014: 230-235.

[8]FANG Jiangxiong, YANG Jie, LIU Huaxiang. Efficient and robust fragments-based multiple kernels tracking[J]. AEU-international journal of electronics and communications, 2011, 65(11): 915-923.

[9]SHEN Chunhua, BROOKS M J, VAN DEN HENGEL A. Fast global kernel density mode seeking: applications to localization and tracking[J]. IEEE transactions on image processing, 2007, 16(5): 1457-1469.

[10]CHANG S. Stochastic peak tracking and the Kalman filter[J]. IEEE transactions on automatic control, 1968, 13(6): 750.

[11]DOUCET A, GORDON N. Efficient particle filters for tracking manoeuvring targets in clutter[C]//Proceedings of IEE Colloquium on Target Tracking: Algorithms and Applications. London: IEEE, 1999: 4/1-4/5.

[12]ZADEH L A. Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic[J]. Fuzzy sets and systems, 1997, 90(2): 111-127.

[13]LIN T Y. Granular computing: fuzzy logic and rough sets[C]//ZADEH L A, KACPRZYK J. Computing with Words in Information/Intelligent Systems 1. Berlin Heidelberg: Physica-Verlag HD, 1999: 183-200.

[14]苗夺谦, 王国胤, 刘清, 等. 粒计算: 过去、现在与展望[M]. 北京: 科学出版社, 2007.

MIAO Duoqian, WANG Guoyin, LIU Qing, et al. Granular computing: past, present and future[M]. Beijing: Science Press, 2007.

[15]徐计, 王国胤, 于洪. 基于粒计算的大数据处理[J]. 计算机学报, 2015, 38(8): 1497-1517.

XU Ji, WANG Guoyin, YU Hong. Review of big data processing based on granular computing[J]. Chinese journal of computers, 2015, 38(8): 1497-1517.

刘翠君,女，1993年生，硕士研究生，主要研究方向为计算机视觉、粒计算等。

赵才荣，男，1981年生，副研究员，博士，主要研究方向为人脸识别、计算机视觉等。

苗夺谦，男，1964年生，教授、博士生导师，博士，主要研究方向为粒计算、粗糙集、中文信息处理等。

Granular mean shift pedestrian tracking algorithm

LIU Cuijun， ZHAO Cairong， MIAO Duoqian， WANG Xuekuan

(College of Electronics and Information Engineering, Tongji University, Shanghai 201804, China)

Mean shift pedestrian tracking that uses a color histogram as its tracking feature has drawbacks, e.g., performance can easily be affected by the introduction of a background color. To solve this problem, the idea of granular computing was introduced into the traditional mean shift pedestrian tracking algorithm, and a new granular mean shift pedestrian tracking algorithm, based on granular computing, is presented. The algorithm blocks the image’s target area with specific granularity to extract color features, then adopts different color channels of granulation on the feature, and finally realizes target tracking under the framework of the mean shift iteration. Compared with other traditional methods the algorithm displays lower computational complexity and is more robust. Experimental results on PETS2009 and CAVIAR databases show that the algorithm achieves a higher tracking accuracy, better robustness and efficiency under color interference, and can track the target pedestrian in real time.

information granules; granular computing; mean shift; feature extraction; pedestrian tracking

10.11992/tis.201605033

网络出版地址：http://www.cnki.net/kcms/detail/23.1538.TP.20160808.0831.022.html

2016-05-30. 网络出版日期：2016-08-08.

国家自然科学基金项目(61273304)；上海市中医药三年行动计划重点项目(ZY3-CCCX-3-6002)

苗夺谦. E-mail：dqmiao@tongji.edu.cn.

TP391

A

1673-4785(2016)04-0433-09