基于不完备信息系统的三角模糊数决策粗糙集
2016-09-27李亚鸽杨宏志徐久成
李亚鸽,杨宏志,徐久成
(1.郑州大学 数学与统计学院,河南 郑州 450001; 2. 河南财经政法大学,河南 郑州 450046; 3. 河南师范大学 计算机与信息工程学院,河南 新乡 453007; 4.新乡学院 数学与信息科学学院,河南 新乡 453007)
基于不完备信息系统的三角模糊数决策粗糙集
李亚鸽1,4,杨宏志2,徐久成3
(1.郑州大学 数学与统计学院,河南 郑州 450001; 2. 河南财经政法大学,河南 郑州 450046; 3. 河南师范大学 计算机与信息工程学院,河南 新乡 453007; 4.新乡学院 数学与信息科学学院,河南 新乡 453007)
在不完备信息系统中,针对用区间值表示一个未知参量时,整个区间内取值机会被认为是均等的,得到的结果可能会产生过大误差的问题,将三角模糊数引入到决策粗糙集中,提出了一种基于不完备信息系统的三角模糊数决策粗糙集。首先,定义了一种描述不完备信息的相似关系;然后,针对不完备信息系统中的缺失值,利用三角模糊数来获取损失函数,构建了三角模糊数决策粗糙集模型;实例表明,本文提出的方法不仅能够弥补用区间数表示的不足,而且可以突出可能性最大的主值,从而减少分类误差。
不完备信息系统;区间值;三角模糊数;决策粗糙集
中文引用格式:李亚鸽,杨宏志,徐久成. 基于不完备信息系统的三角模糊数决策粗糙集[J]. 智能系统学报, 2016, 11(4): 449-458.
英文引用格式:LI Yage , YANG Hongzhi, XU Jiucheng. Triangular fuzzy number decision-theoretic rough sets under incomplete information systems[J]. CAAI Transactions on Intelligent Systems, 2016, 11(4): 449-458.
在现实生活中,由于测量误差、数据获取能力不足等原因,使得大量的信息系统都是不完备的[1]。一般来说,不完备信息系统(incomplete information systems, IIS)中的未知属性值有3种不同的情况。一种是未知属性值是被遗漏的,但又确实存在的[2]。根据这样的解释,Kryszkiewicz构建满足自反性和对称性的容差关系[3],并研究了IIS中的知识约简问题;基于容差关系,王国胤等[1]提出了限制容差关系;杨习贝等[4]给出了一种可变精度分类关系,对限制容差关系进行了扩展;一种是未知属性值被认为是丢失的,不允许被比较[5],据此,Stefanowski等构建了非对称相似关系[6],并建立了近似集的概念;另外一种是未知属性值被认为是暂时性缺失。
决策粗糙集是20世纪90年代由Yao提出的一种重要的粗糙集模型[7],该理论的核心内容是通过分析比较各种决策的风险损失,找出最小风险损失决策,以此作为把对象划分到正域、负域和边界域的依据。贾修一等[8]提出了一种基于决策风险最最小化的属性约简定义,它要求在约简后的属性集合上所做出的决策风险小;王国胤等[9]对国内外有关决策粗糙集模型进行了综述和分析;Li等[10]根据决策者的不同风险偏好,给出了乐观决策、悲观决策与中性决策的多角度决策粗糙集模型;叶东毅等[11]提出了基于模糊数风险最小化的拓展决策粗糙集模型;此外,决策粗糙集已在邮件信息过滤系统、文本聚类和分类、石油开采中得到了较好应用[12-16]。
然而,在已有对决策粗糙集的研究中,代价敏感损失函数大都由专家提供。考虑到人为判断的模糊性,单值损失函数存在很大误差,损失函数应具有一定的伸缩性,为此,刘盾等[17]提出区间决策粗糙集,讨论了用区间值来刻画损失函数;考虑到信息系统的不完备性,马兴斌等[18]讨论了不完备信息系统中的多重代价决策粗糙集;刘盾等[19]将不完备信息引入到区间决策粗糙集中,构建了一个混合信息知识表,用以处理IIS中的三支决策问题,但是这仍具有一定的误差,特别地,在IIS中,用区间数表示一个未知参量时,整个区间内取值机会被认为是均等的,得到的结果可能会产生过大误差。而在三角模糊数区间取值中,主值a的取值机会最大,由a靠近上限、下限取值可能性递减。因此,使用三角模糊数进行不确定性值的评判,不仅能够突出取可能性最大的主值,而且可以弥补用区间数表示的不足。基于此,本文在IIS的基础上提出了使用三角模糊数来改善只用上下限表示的区间数取值,构建了三角模糊数决策粗糙集模型。
1 基础知识
1.1决策粗糙集
决策粗糙集[20-21]模型利用两个状态集和3个行动集描述决策过程。状态集Ω= {X,X}分别表示某事件属于X和不属于X,行动集A={aP,aB,aN}分别表示接受某事件、延迟决策和拒绝某事件3种行动。考虑到采取不同行动会产生不同的损失,用λPP、λBP、λNP分别表示当x属于X时,采取行动aP、aB、aN下的损失;用λPN、λBN、λNN分别表示当x不属于X时,采取行动aP、aB、aN下的损失。因此采取aP、aB、aN3种行动下的期望损失可分别表示为
(1)式中:[x]为样本在属性集下的等价类,P(X| [x])和P(X| [x])分别表示将等价类[x]划分为X和X的概率。根据贝叶斯决策准则,需要选择期望损失最小的行动集作为最佳行动方案,于是得到如下3条决策规则:
P) 若R(aP|[x]) ≤R(aB|[x])和R(aP|[x]) ≤R(aN|[x]同时成立,那么xPOS(X);
B) 若R(aB|[x]) ≤R(aP|[x])和R(aB|[x]) ≤R(aN|[x])同时成立,那么xBND(X);
N) 若R(aN|[x]) ≤R(aP|[x])和R(aN|[x]) ≤R(aB|[x]同时成立,那么xNEG(X)。
由于P(X| [x])+P(X| [x])=1,所以上述规则只与概率P(X| [x])和相关的损失函数λ有关。基于常识,做出正确决策产生的损失要小于做出错误决策产生的损失,故有0 ≤λPP≤λBPλNP,0 ≤λNN≤λBNλPN。基于这两个条件,从规则P)~N)可以获得以下3个阈值
(2)基于上述3个阈值,规则P)~N)可简明表示为
P′) 若P(X|[x]) ≥α且P(X|[x]) ≥γ,则xPOS(X);
B′) 若P(X|[x]) ≤α且P(X|[x]) ≥β,则xBND(X);
N′) 若P(X|[x]) ≤β且P(X|[x]) ≤γ,则xNEG(X)。
1.2三角模糊数
模糊集作为精确数值的一种扩展形式,被用于处理模糊、不精确和不确定性决策问题。在模糊集理论中,隶属函数是它的一个最基本元素。在隶属函数中,三角模糊数是其中具有代表性的一个。
定义2[22]实数R上的模糊数a=(l, m, u)是一个三角模糊数,其中,l、m、u为实数,且lλmλu,m称为三角模糊数a的主值,l与u分别称为a的下界和上界。
模糊数a的隶属函数的表达式可表示为
(3)当l=m或m=u时,三角模糊数就转变为区间数,由此可见区间数是三角模糊数的一个特例。在区间数取值中,上下限的各个取值可以认为是机会均等的,而在三角模糊数区间取值中,主值a的取值机会最大,而由a靠近上限、下限的取值可能性递减。
对于任意两个模糊三角数a1=(l1,m1,u1),a2=(l2,m2,u2),根据扩展定理[24]相应的运算规则如下:
1)a1+a1=(l1+l2,m1+m2,u1+u2);
2)a1-a2=(l1-l2,m1-m2,u1-u2);
3) a1a2=(l1l2,m1m2,u1u2);
4)a1/a2=(l1/u2,m1/m2,u1/l2);
5) λ a2=(λ l2, λ m2, λ u2), λR且λ >0。
2 基于IIS的三角模糊数决策粗糙集
2.1不完备信息系统
定义1[23]不完备信息系统IIS= (U, AT,V,f)。其中,U是一个被称为论域的对象集合;AT是非空有限的属性集合;对于aAT,有a:UVa,其中Va是属性a的值域(包括遗漏型空值和缺失型空值)。属性值域集合V=UaATVa,f为信息函数,对于aA,xU,有f(x,a)Va。在本文中,IIS中所有的未知值都被认为是被遗漏的。
2.2相似度及相关知识
在IIS= (U, AT,V,f)中,V=Va{},表示未知的值。陈圣兵等[25]在不完备信息系统中,分析并讨论了空值相等的概率问题。基于文献[25],我们提出了在不完备信息系统中相似度的概念。
定义3 不完备信息系统IIS= (U, AT,V,f)。U={x1,x2, …,xn}为n个对象的集合,A={a1,a2, …,am}为m个属性的集合。xi,xj, 由ai确定的相似度关系Sai(xi,xj)为
(4)

任意两个对象xi、xj的相似度S(xi,xj)为
(5)
定义4不完备信息系统IIS= (U, AT,V,f)。L[0, 1],相似关系SRAL为SRA的L-截集,其中L称为阈值或置信水平,即

根据相似度的定义(5),基于L-截集相似关系(6),我们定义在IIS中的两个近似和3个决策区域。
定义5 不完备信息系统IIS= (U, AT,V,f)。xU,令0<β≤α≤1,基于L-截集相似关系的下、上近似为
(7)
(8)
相对应的3个决策区域分别为
(9)
2.3整数值排序法
整数值排序法是通过把模糊数直接转化成单个实数,然后依据实数大小来判定模糊数的次序。这种排序方法,涉及到决策者的风险偏好。根据Kumar A[26]的研究结论,三角模糊数r(a)的排序函数为
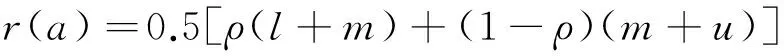
(10)式中:ρ是决策者的风险偏好指数,反映出决策者的乐观程度。在式(10)中ρ值越大意味着决策者越乐观,即悲观决策者会高估损失值,而乐观决策者则会低估损失值。特别地,当ρ= 0和ρ= 1时,r(a)的值分别代表了悲观决策者和乐观决策者的观点。
2.4基于IIS的三角模糊数决策粗糙集的模型实现
根据贝叶斯决策过程,运用三角模糊数,不同状态对应的三角模糊数损失值如表1所示。

表1 不同状态下对应的三角模糊数损失值
在表1中,λPP=(lPP,mPP,uPP)、λBP=(lBP,mBP,uBP)、λNP=(lNP,mNP,uNP)分别表示当x属于X时,采取行动aP、aB、aN下的损失;用λPN=(lPN,mPN,uPN)、λBN=(lBN,mBN,uBN)、λNN=(lNN,mNN,uNN)分别表示当x不属于X时,采取行动aP、aB、aN下的损失。根据决策粗糙集的基本条件,假定损失值满足以下条件
因此采取aP、aB、aN3种行动下的期望损失可分别表示为
(11)根据贝叶斯决策准则,需要选择期望损失最小的行动集作为最佳行动方案,于是可得到如下3条决策规则:



在本文,我们选取整数值排序方法来研究三角模糊数决策粗糙集。基于式(10),各期望损失值可以分别计算得到
其中
故得到如下3条决策规则:



由此,可推导出三角模糊数决策粗糙集的3个阈值,其结果为
(12)考虑到决策者的风险态度,基于决策粗糙集依次提出乐观决策模型、中性决策模型和悲观决策模型。类似于Li、Zhou的思想[10],在整数值排序方法中决策者的风险态度指数是三角模糊数排序的重要要素,它会影响到阈值的取值。特别地,当ρ=1,对于乐观决策者,其阈值可以表达为
当ρ=0,对于悲观决策者,其阈值可以表达为
鉴于Yao[27]的讨论结果,首先考虑决策规则(B)中存在αβ的情况,即
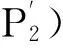
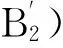
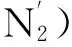
对于乐观决策者,此时ρ=1,所对应的三支决策规则为



对于悲观决策者,此时ρ=0,所对应的三支决策规则为



此外,为了保证研究的完备性,决策规则(B)还有另一种情况,即:
该条件蕴含着0≤α<γ<β≤1,此时,通过权衡可以得到以下简化规则:

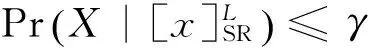
3 案例分析
医学诊断是一种根据病人现有症状来判断所得疾病类列的决策过程,在下面的讨论中,以医学流感诊断决策表S=
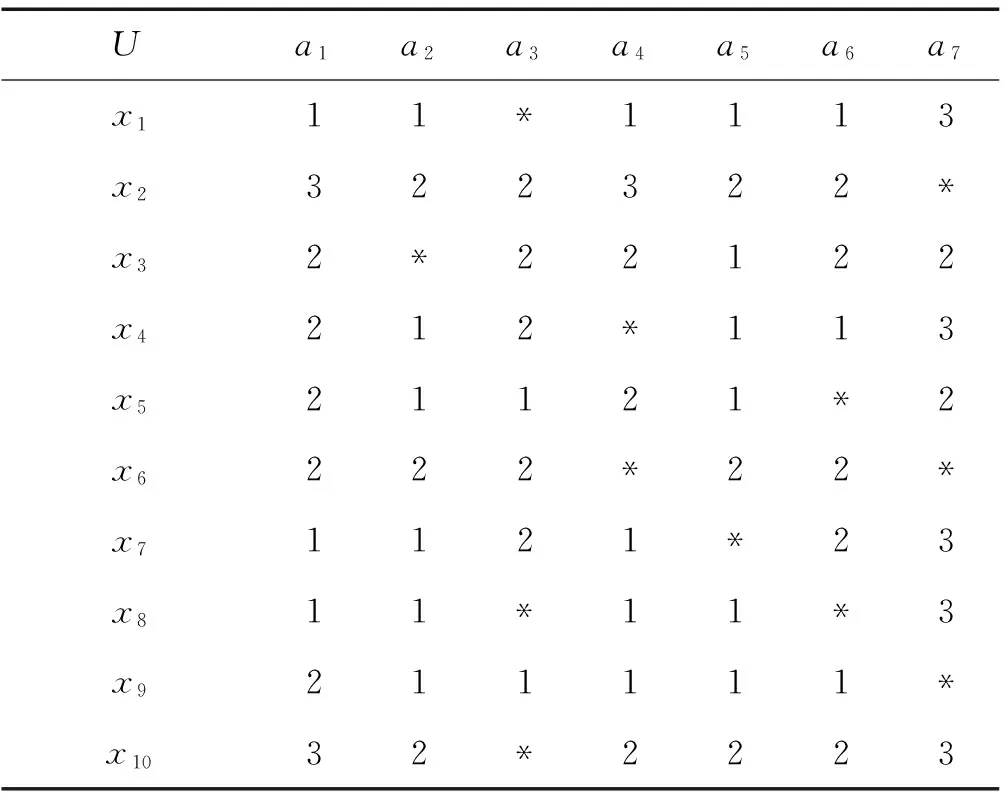
表2 病人患病的实际情况
为描述方便,在表2中,根据医生的经验,对每个属性所对应值的大小有如下定义:
温度a1:1代表高,2代表较高,3代表正常;
咳嗽a2:1代表是,2代表不是;
流鼻涕a3:1代表是,2代表不是;
头疼a4:1代表很严重,2代表有点严重,3代表不严重;
恶心a5:1代表是,2代表不是;
有痰a6:1代表有,2代表没有;
肌肉疼a7:1代表很严重,2代表有点严重,3代表不严重,*代表缺失值。
首先,根据医生的经验给出三角模糊数的损失区间,如表3所示。然后,根据式(4),计算对象U中任意两位患者xi,xj的相似度,结果如表4所示。

表3 病人的综合评估损失情况
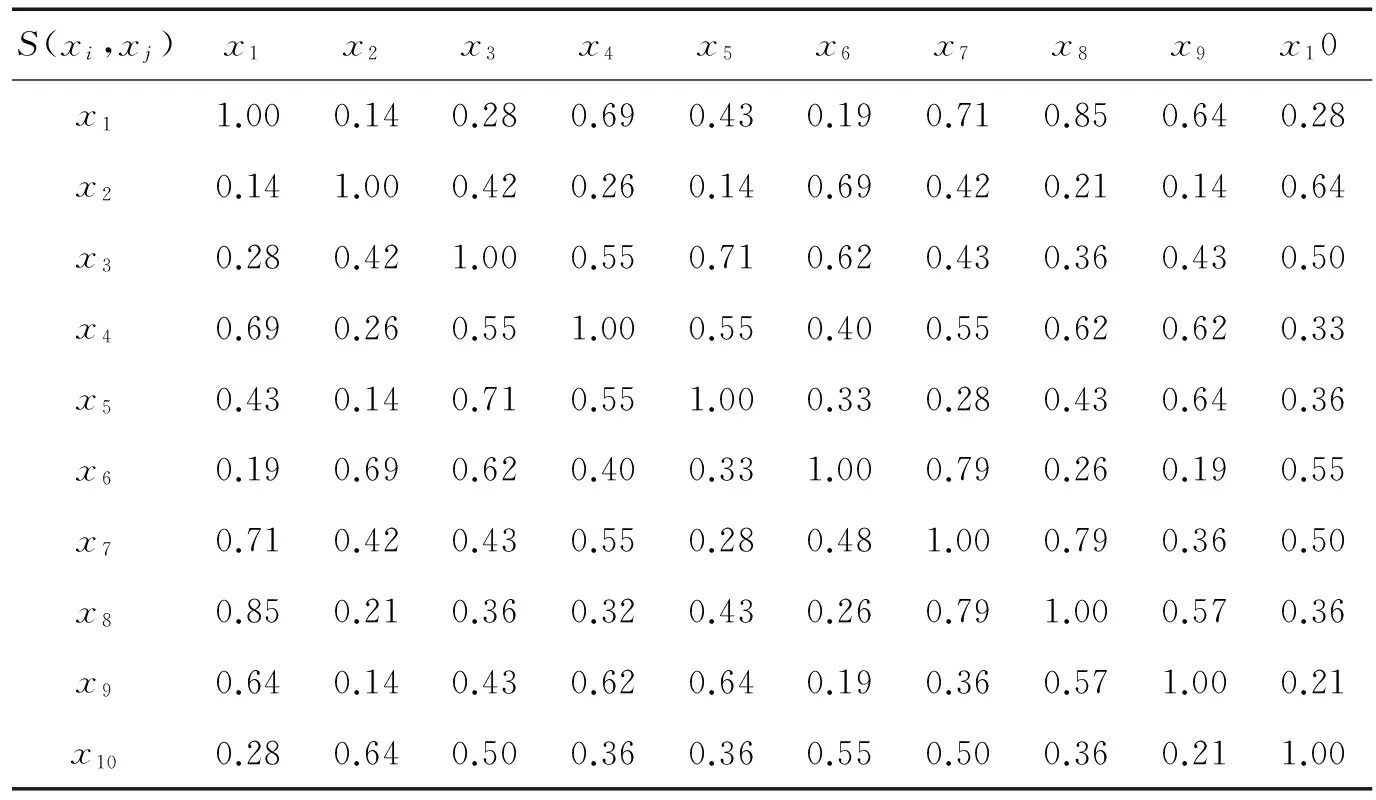
表4 各个病人之间相似度表示
在表3中,令L=0.5+ε(ε是正的无穷小数),基于相似度可得xi的等价类:
根据医生的经验,集合X={ x1, x4, x5, x7, x8}时,这些患者得流感的概率相对较高。根据表2,每位患者得流感的条件概率如下:
根据2.2节整数排序法的三角模糊数r(a)的排序函数式(10),当ρ= 0和ρ= 1时,r(a)的值分别代表悲观决策者和乐观决策者的观点。根据式(12)可得各个病人的三角模糊数决策粗糙集相关阈值,计算结果如表5所示。

表5 各个病人的相关阈值计算结果
表5列出了每位病人在风险偏好者决策准则、风险厌恶者决策准则下,α、β和γ的取值情况。可以看出,α2较α1取值普遍大,β2较β1取值普遍小,这说明悲观主义者厌恶风险,它通过较大的α 值和较小的β 值避免生病被延误的概率;而乐观主义者偏好风险,它通过较小的α 值和较大的β 值获取无病的概率。
根据三角模糊数决策粗糙集中的决策规则,在决策判定过程中需要比较条件概率Pr(X|[xi]SRL)和阈值αi、βi的大小。当L= 0.5+ε时,乐观决策者和悲观决策者的决策结果如表6所示。

表6 决策结果
从表6可以看出,在乐观决策者看来,{x1,x4,x5,x7,x8,x9}POS(X),{x2,x6,x10}NEG(X),{x3}BND(X)。但在悲观决策者看来,{x1,x4,x5,x7,x8,x9POS(X),{x2,x3,x6,x10}NEG(X)。通过与X={x1,x4,x5,x7,x8}对比可以发现,x3不是诱发患者患病的主要因素,但对于乐观决策者来说,还需对它进行进一步的诊断。x9也不是诱发患者患病的主要因素,但乐观决策者和悲观决策者认为都需要进一步的诊断。因此,决策粗糙集能为现实的决策系统提供了一种修正误分类错误的方法。
在上述实例中,我们求得的相似关系及条件概率是在L=0.5+ε的基础上进行讨论的。下面我们将探讨L[0.5, 1],步长0.1时,与之相对应的乐观决策者和悲观决策者的决策,结果如表7所示。

表7 L取不同的值所对应的决策结果
从表7可以看出,随着决策偏好的粒度L的变化,决策者的选择会有一定的变化。当L=0.7时,乐观决策者和悲观决策者认为x3、x6需要进一步的诊断,才能确诊。然而当L≥0.8时,乐观决策者和悲观决策者认为x3、x6不需要进一步诊断,即可视为无患病者。且随着粒度的增大,决策者的决策趋于稳定的状态。
在IIS中,基于已给出的相似关系及已求得的条件概率,取三角模糊数的端点值作为区间值,将基于不完备信息系统的三角模糊数决策粗糙集与文献[17]中的区间决策粗糙集方法作对比,在测试数据集上进行实验,根据文献[17]可得相对应的各个病人的相关阈值,乐观和悲观决策者的决策结果,及当L[0.5, 1],步长0.1时,随着L粒度的变化,与之对应的乐观和悲观决策者的决策,结果如表8~10所示。
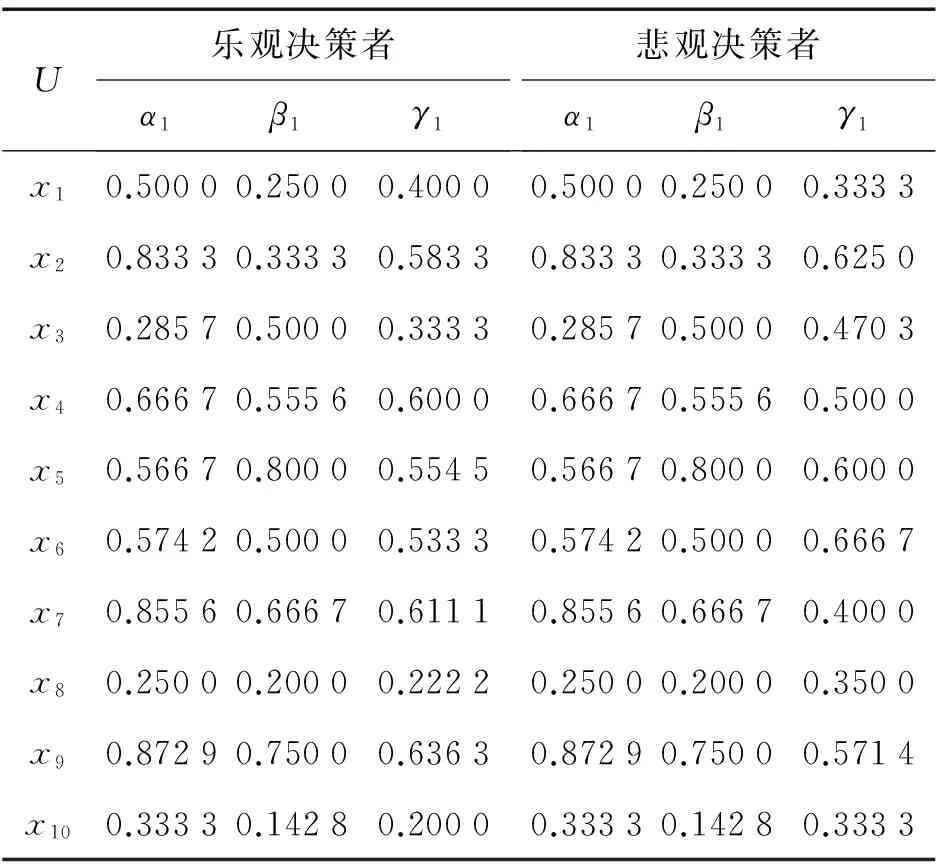
表8 各个病人的相关阈值计算结果
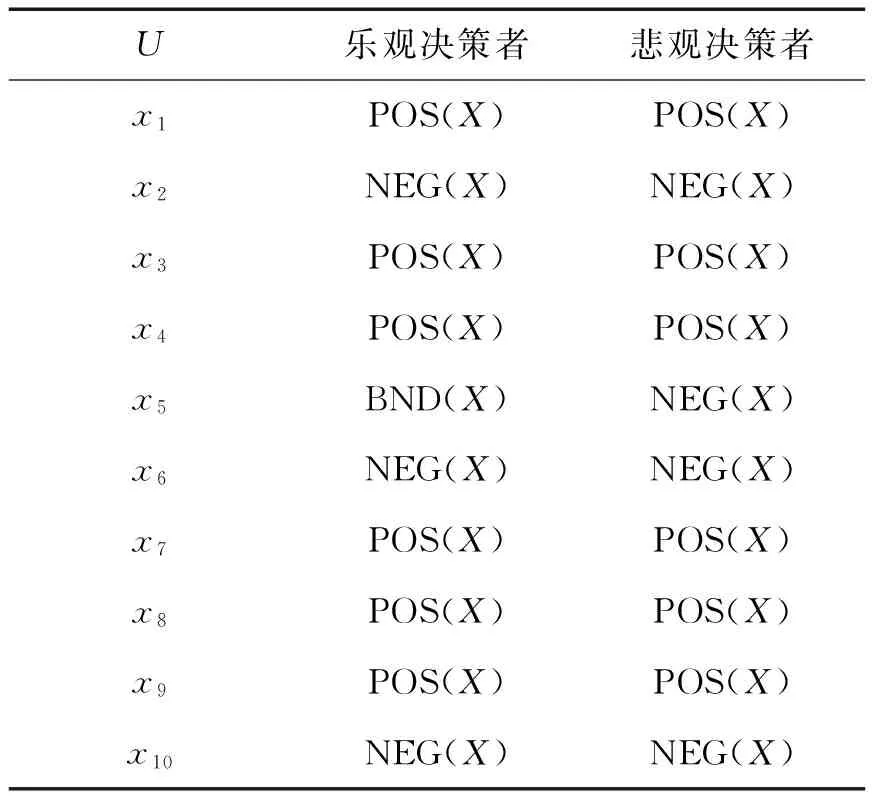
表9 决策结果
从表9可以看出,取区间值作为基础数据集时,在乐观决策者看来,{x1,x3,x4,x7,x8,x9}POS(X), {x2,x6,x10}NEG(X),{x5}BND(X)。但在悲观决策者看来,{x1,x3,x4,x7,x8,x9}POS(X),{x2,x5,x6,x10}NEG(X)。通过与表6及集合X={x1,x4,x5,x7,x8}得流感的概率相对较高的患者对比可以发现,x5是诱发患者患病的主要因素,但是悲观决策者认为不需要进一步的诊断。而x3不是诱发患者患病的主要因素,但是对于取区间值的乐观决策者和悲观决策者来说,都需对它进行进一步的诊断。

表10 L取不同的值所对应的决策结果
从表10可以看出,当L≥0.8时,乐观和悲观决策者的决策结果趋于稳定,其中x9不是诱发患者患病的主要因素,但是对于取区间值的乐观和悲观决策者来说,都需对它进行进一步的诊断。与采用三角模糊数方法相比,采用区间值分析与实际经验值会产生较大的误差。
4 结束语
本文基于IIS,从决策粗糙集出发,利用三角模糊数来设定损失函数,首先提出一种描述不完备信息的相似关系。然后,针对IIS中缺失值,借助三角模糊数的运算法则,利用三角模糊数来获取损失函数,构建出三角模糊数决策粗糙集的基础模型。通过实例可知,不同于区间数决策粗糙集的决策机制,利用三角模糊数来获取损失函数,不仅能弥补使用区间参数时无法考虑区间内取值机会不等的问题,而且能更加细致地描述各个参量,使决策结果更加符合实际应用。下一个阶段,将着重研究其他不确定环境下相应的扩展粗糙集模型的建立,如损失函数是随机数且服从正态分布等情况下的研究。
[1]王国胤. Rough集理论在不完备信息系统中的扩充[J]. 计算机研究与发展, 2002, 39(10): 1238-1243.
WANG Guoyin. Extension of rough set under incomplete information systems[J]. Journal of computer research and development, 2002, 39(10): 1238-1243.
[2]GRZYMALA-BUSSE J W. On the unknown attribute values in learning from examples[C]//RAS Z W, ZEMANKOVA M. Proceedings of the 6th International Symposium on Methodologies for Intelligent Systems (ISMIS-91). Berlin, Heidelberg: Springer-Verlag, 1991, 542: 368-377.
[3]KRYSZKIEWICZ M. Rough set approach to incomplete information systems[J]. Information sciences, 1988, 112(1/2/3/4): 39-49.
[4]杨习贝, 杨静宇, 於东军, 等. 不完备信息系统中的可变精度分类粗糙集模型[J]. 系统工程理论与实践, 2008, 28(5): 116-121.
YANG Xibei, YANG Jingyu, YU Dongjun, et al. Rough set model based on variable parameter classification in incomplete information systems[J]. Systems engineering-theory & practice, 2008, 28(5): 116-121.
[5]GRZYMALA-BUSSE J W, WANG A Y. Modified algorithms LEM1 and LEM2 for rule induction from data with missing attribute values[C]//Proceeding of the Fifth International Workshop on Rough Sets and Soft Computing (RSSC'97) at the Third Joint Conference on Information Sciences (JCIS'97). Research Triangle Park, NC, 1997: 69-72.
[6]STEFANOWSKI J, TSOUKIàS A. Incomplete information tables and rough classification[J]. Computational intelligence, 2001, 17(3): 545-566.
[7]YAO Y Y, WONG S K M. A decision theoretic framework for approximating concepts[J]. International journal of man-machine studies, 1922, 37(6): 793-809.
[8]贾修一, 商琳, 陈家骏. 决策风险最小化属性约简[J]. 计算机科学与探索, 2011, 5(2): 155-160.
JIA Xiuyi, SHANG Lin, CHEN Jiajun. Attribute reduction based on minimum decision cost[J]. Journal of frontiers of computer science & technology, 2011, 5(2): 155-160.
[9]于洪, 王国胤, 姚一豫. 决策粗糙集理论研究现状与展望[J]. 计算机学报, 2015, 38(8): 1628-1639.
YU Hong, WANG Guoyin, YAO Yiyu. Current research and future perspectives on decision-theoretic rough sets[J]. Chinese journal of computers, 2015, 38(8): 1628-1639.
[10]LI Huaxiong, ZHOU Xianzhong. Risk decision making based on decision-theoretic rough set: a three-way view decision model[J]. International journal of computational intelligence systems, 2011, 4(1): 1-11.
[11]衷锦仪, 叶东毅. 基于模糊数风险最小化的拓展决策粗糙集模型[J]. 计算机科学, 2014, 41(3): 50-54, 75.
ZHONG Jinyi, YE Dongyi. Extended decision-theoretic rough set models based on fuzzy minimum cost[J]. Computer science, 2014, 41(3): 50-54.
[12]LIU Dun, LI Huaxiong, ZHOU Xianzhong. Two decades’research on decision-theoretic rough sets[C]//Proceeding of the 9th IEEE International Conference on Cognitive Informatics. Beijing: IEEE, 2010: 968-973.
[13]李华雄, 刘盾, 周献中. 决策粗糙集模型研究综述[J]. 重庆邮电大学学报: 自然科学版, 2010, 22(5): 624-630.
LI Huaxiong, LIU Dun, ZHOU Xianzhong. Rewiew on decision-theoretic rough set model[J]. Journal of Chongqing university of posts and telecommunications: natural science edition, 2010, 22(5): 624-630.
[14]李华雄, 周献中, 李天瑞, 等. 决策粗糙集理论及其研究进展[M]. 北京: 科学出版社, 2011.
LI Huaxiong, ZHOU Xianzhong, LI Tianrui, et al. Decision-theoretic rough sets theory and recent research[M]. Beijing: Science Press, 2011.
[15]刘盾, 姚一豫, 李天瑞. 三枝决策粗糙集[J]. 计算机科学, 2011, 38(1): 246-250.
LIU Dun, YAO Yiyu, LI Tianrui. Three-way decision-theoretic rough sets[J]. Computer science, 2011, 38(1): 246-250.
[16]LIANG Decui, PEDRYCZ W, LIU Dun, et al. Three-way decisions based on decision-theoretic rough sets under linguistic assessment with the aid of group decision making[J]. Applied soft computing, 2015, 29: 256-269.
[17]刘盾, 李天瑞, 李华雄. 区间决策粗糙集[J]. 计算机科学, 2012, 39(7): 178-181, 214.
LIU Dun, LI Tianrui, LI Huaxiong. Interval-valued decision-theoretic rough sets[J]. Computer science, 2012, 39(7): 178-181, 214.
[18]马兴斌, 鞠恒荣, 杨习贝, 等. 不完备信息系统中的多重代价决策粗糙集[J]. 南京大学学报: 自然科学版, 2015, 51(2): 335-342.
MA Xingbin, JU Hengrong, YANG Xibei, et al. Multi-cost based decision-theoretic rough sets in incomplete information systems[J]. Journal of Nanjing university: natural sciences, 2015, 51(2): 335-342.
[19]LIU Dun, LIANG Decui, WANG Changchun. A novel three-way decision model based on incomplete information system[J]. Knowledge-based systems, 2016, 91: 32-45.
[20]YAO Y Y, WONG S K M. A decision theoretic framework for approximating concepts[J]. International journal of man-machine studies, 1992, 37(6): 793-809.
[21]YAO Yiyu. Decision-theoretic rough set models[M]//YAO Jingtao, LINGRAS P, WU Weizhi, et al. Rough Sets and Knowledge Technology. Berlin Heidelberg: Springer, 2007, 4481: 1-12.
[22]唐国春. 模糊排序中的面积模糊度[J]. 上海第二工业大学学报, 1999, 16(2): 48-55.
TANG Guochun. The area degree of fuzziness in fuzzy scheduling[J]. Journal of Shanghai second polytechnic university, 1999, 16(2): 48-55.
[23]KRYSZKIEWICZ M. Rough set approach to incomplete information systems[J]. Information sciences, 1998, 112(1/2/3/4): 39-49.
[24]KAUFMAN A, GUPTA M M. Introduction to fuzzy arithmetic: theory and application[M]. New York: Van Nostrand Reinhold, 1985.
[25]陈圣兵, 李龙澍, 纪霞, 等. 不完备信息系统中基于集对相似度的粗集模型[J]. 计算机科学, 2010, 37(7): 186-190.
CHEN Shengbing, LI Longshu, JI Xia, et al. Extension of rough set model based on SPA similarity degree in incomplete information systems[J]. Computer science, 2010, 37(7): 186-190.
[26]KUMAR A, SINGH P, KAUR A, et al. A new approach for ranking of L-R type generalized fuzzy numbers[J]. Expert systems with applications, 2011, 38(9): 10906-10910.
[27]YAO Yiyu. The superiority of three-way decisions in probabilistic rough set models[J]. Information sciences, 2011, 181(6): 1080-1096.

李亚鸽,女,1990年生,硕士研究生,主要研究方向为粗糙集、粒计算、三支决策。

杨宏志,男,1962年生,教授,博士,主要研究方向为粗糙集、概念格、粒计算。杨宏志教授长期从事应用数学的教学与研究工作,先后发表学术论文30余篇,出版著作2部,承担并完成省级项目8项。

徐久成,男,1964年生,教授,博士生导师,主要研究方向为数据挖掘、粒计算与知识获取、生物信息学等。发表学术论文100余篇,其中被SCI收录14篇,被EI收录30余篇;出版专著1部,主编国家“十一.五”、“十二.五”规划统编教材3部。获河南省自然科学优秀学术论文一等奖3项、河南省高等教育省级教学成果一等奖2项,河南省教育厅科技成果一等奖1项。
Triangular fuzzy number decision-theoretic rough sets under incomplete information systems
LI Yage1,4, YANG Hongzhi2, XU Jiucheng3
(1. School of Mathematics and Statistics, Zhengzhou University, Zhengzhou 450001, China; 2. Henan University of Economics and Law, Zhengzhou, Zhengzhou 450046, China; 3. College of Computer and Information Engineering, Henan Normal University, Xinxiang 453007, China; 4. Department of Mathematics and Information Science,Xinxiang University, Xinxiang 453007,China)
Aiming at the problems that when using an interval value to represent an unknown parameter in an incomplete information system, the opportunity to obtain the value over the whole interval is considered to be equal, but the result may cause an over-large error. In order to solve this problem, a triangular fuzzy number was introduced into decision-theoretic rough sets, and a triangular fuzzy decision-theoretic rough set under incomplete information systems is proposed. Firstly, a new similarity relation was defined to describe incomplete information systems. Then, in view of the missing values, a model of triangular fuzzy number decision-theoretic rough sets was constructed to obtain the loss function. Finally, examples show that the proposed method not only makes up for deficiency in representation of the interval value, but also highlights the main value most likely to reduce the classification error.
incomplete information system; interval value; triangular fuzzy number; decision-theoretic rough sets
10.11992/tis.201606016
网络出版地址:http://www.cnki.net/kcms/detail/23.1538.TP.20160808.0831.026.html
2016-06-03. 网络出版日期:2016-08-08.
国家自然科学基金项目(61370169, 61402153);河南省科技攻关重点项目(142102210056, 162102210261);河南省高等学校重点科研项目(16A520057).
李亚鸽. E-mail:liyagezzu@163.com.
TP18
A
1673-4785(2016)04-0449-10
