效用三支决策模型
2016-09-27张楠姜丽丽岳晓冬周杰
张楠,姜丽丽,岳晓冬,周杰
(1. 烟台大学 计算机与控制工程学院,山东 烟台 264005; 2. 上海大学 计算机工程与科学学院,上海 200444; 3. 中联重科股份有限公司 麓谷工业园研发中心,湖南 长沙 410205)
效用三支决策模型
张楠1,姜丽丽1,岳晓冬2,周杰3
(1. 烟台大学 计算机与控制工程学院,山东 烟台 264005; 2. 上海大学 计算机工程与科学学院,上海 200444; 3. 中联重科股份有限公司 麓谷工业园研发中心,湖南 长沙 410205)
风险型决策通常受主观和客观两方面因素影响,决策过程中不仅需要遵从客观存在的风险信息,而且需要发挥决策者的主观能动性。为了在决策过程中引入决策者对于风险的主观态度,本文把效用理论应用于三支决策模型,通过将风险损失函数扩展为效用函数提出了基于效用的三支决策模型。研究了效用与对象的概率之间的单调关系,给出了效用三支决策中正域效用、边界域效用与负域效用的计算方法。最后,通过算例对提出的效用三支决策模型进行了有效地分析。该模型是经典三支决策模型的扩展,为三支决策模型中风险的主观量化研究提供了有益探索。
效用理论;三支决策;粗糙集;人工智能;风险决策
中文引用格式:张楠,姜丽丽,岳晓冬,等. 效用三支决策模型[J]. 智能系统学报, 2016, 11(4): 459-468.
英文引用格式:ZHANG Nan, JIANG Lili, YUE Xiaodong, et al. Utility-based three-way decisions model[J]. CAAI Transactions on Intelligent Systems, 2016, 11(4): 459-468.
在实际应用中,由于决策信息的不精确或者不完备,人们很难简单地采用接受与拒绝两种方式进行决策。通过推广两支决策到三支决策,加拿大Regina大学的Yao提出了三支决策理论[1](three-way decisions, TWD)。三支决策理论将不承诺决策(延迟决策)作为信息贫乏不足以决定接受或者拒绝时的第3种决策方式。因为考虑到决策过程中的不确定性因素,三支决策提供了接受、拒绝与不承诺3种决策方式,更加符合人类的认知模式。近年来,三支决策理论发展迅速,广泛地应用于机器学习[2-9]、认知计算[10-13]、数据挖掘[14-17]、模式识别[18]与人工智能[19-20]等研究领域。
针对经典粗糙集模型缺乏容错能力,Yao[21]通过引入概率包含关系在1990年提出了决策粗糙集(decision-theoretic rough sets, DTRS)模型;Yu等[22]提出了一种基于决策粗糙集的聚类模式代价评估的方法;文献[23]结合三支决策思想,提出了一种新的无标记数据学习模型TWD-SSL。该模型解决了部分标记数据的属性约简和分类学习问题。考虑到粗糙集理论中的正区域、负区域与边界域形成的接受、拒绝与延迟3种决策方式,刘盾[24]系统介绍了基于粗糙集的三支决策模型的理论、方法与应用;基于决策的最小风险;Jia等[25]给出了决策粗糙集模型下最小化决策风险的属性约简定义并提出了一种启发式的最小风险约简算法;Li等[26]定义了决策粗糙集的正域约简并提出了一种正区域约简的启发式算法,该算法可以较好地保持属性约简后正域的非减特征;Qian等[27]提出了多粒度决策粗糙集(multigranulation decision-theoretic rough sets, MDRS)。 多粒度决策粗糙集提供了一种多粒度粗糙集模型的泛化框架,许多现有的多粒度粗糙集模型可以从多粒度决策粗糙集模型中导出;通过扩展单一代价损失矩阵到多代价损失矩阵,文献[28]中提出了θ-决策粗糙集模型。基于提出的模型,分别给出了最小化与最大化的可能代价。定义了决策单调与代价标准两种约简目标,并给出了相应的启发式约简算法;于洪等[29]从决策粗糙集需要解决的几个基本问题出发,系统总结了国内外决策粗糙集研究的现状,分析了存在的挑战并深入探讨了未来发展的研究方向;结合了三支决策与形式概念分析,文献[30]提出了三支概念与三支概念格,三支概念与三支概念格扩展了经典形式概念与概念格并为三支决策提供了一种新的计算模型。
决策过程是客观存在与主观发挥的结合体,不仅要遵从决策系统客观存在的风险信息,而且需要考虑决策者关于风险的态度,发挥决策者本身的主观能动性,使得决策模型更加符合现实决策问题。效用[31]是经济学中的一个抽象概念,用以度量决策者对决策方案的收益或者损失的直接反应与感觉,是决策者自身价值观在决策过程中的综合体现,反映了决策者对待风险的态度。将效用值的概念引入三支决策模型,通过将风险损失函数扩展为效用函数,提出了基于效用的三支决策模型(utility-based three-way decisions,UTWD)。效用三支决策模型可以有效的将决策者的主观能动性(风险态度)考虑到三支决策模型中,是经典三支决策模型的有益扩展,并为三支决策模型中的主观决策量化与度量提供了思路。
1 经典三支决策模型
本节主要介绍Pawlak粗糙集模型及三支决策粗糙集模型的基本概念。对于近似空间(U,A),A=C∪D且C∩D=∅。其中U是论域,为一个有限非空对象集,C是条件属性集,D是决策属性集。论域U关于等价关系C的划分记为π=U/C。[x]∈π表示由对象x在等价关系C下定义的等价类。设子集X⊆U,则X的上、下近似表示如下:

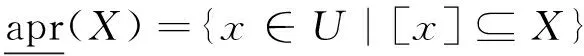
在Pawlak粗糙集中,由集合的交集非空和集合的包含来分别定义集合的上近似和下近似。基于X的上、下近似,可以把论域U划分成3个互不相交的区域:正域POS(X)、边界域BND(X)和负域NEG(X),表示如下:
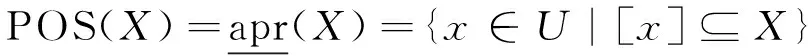
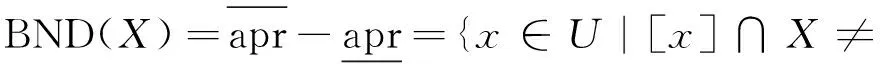
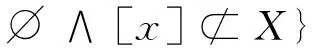
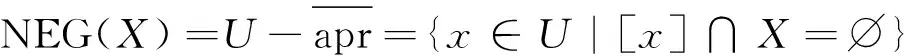
通过将概率引入Pawlak粗糙集中,形成概率粗糙集。令条件概率公式P(X|[x])=|X∩[x]|∕|[x]|表示一个对象以其属于[x]为前提,同时又属于X的条件概率。这样便得到正域POS(X)、边界域BND(X)、负域NEG(X)的概率形式的等价表示:
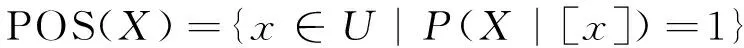
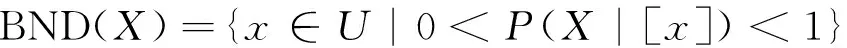
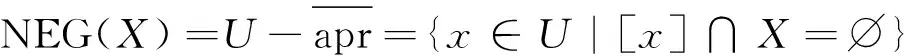
在Pawlak粗糙集中用1和0对3个域进行划分,但划分标准过于严格,缺少一定的容错能力。为解决这个问题,三支决策粗糙集引入一对阈值α和β来替代1和0,其中0≤β<α≤1。当α=1,β=0时,便退化为Pawlak粗糙集。引入阈值(α,β)后,X的(α,β)-上、下近似表示如下:
与Pawlak粗糙集划分相似,在三支决策粗糙集,基于X的(α,β)-上、下近似,得到正域POS(α,β)(X),边界域BND(α,β)(X)和负域NEG(α,β)(X),分别表示如下:
阈值(α,β)可通过专家经验给定或者根据损失函数进行计算获得。在三支决策中,正域对应的规则称为正规则,表示判定决策方案为接受;边界域对应的规则称为边界规则,表示判定决策方案为延迟;负域对应的规则称为负规则,表示判定决策方案为拒绝。
2 效用三支决策模型
2.1效用理论
人们往往根据事件的期望值进行决策,但某些时候并不能真实反映现实决策问题。如对于包含两种状态变量的两种决策方案Γ1={0.5/50,0.5/(-6)}和Γ2={1/20,0/0},其中0.5/50表示在状态1下收益为50且状态1发生的概率为0.5,0.5/(-6)表示在状态2下收益为-6且状态2发生的概率为0.5,方案Γ2类似说明。可以得到,方案Γ1的期望为22,方案Γ2的期望为20。显然方案Γ1的期望收益大于方案Γ2,依据期望收益最大准则,方案Γ1将被采取。但实际中人们却倾向采取方案Γ2,这是因为方案Γ2收益较大并且不承担任何风险。
风险型决策的结果通常会受到主客观两方面因素影响,不仅要遵从客观存在的信息,而且要发挥决策者的主观能动性。效用便是决策者主观意识的具体体现。效用值[31]是一抽象概念,表示所获得的满足程度,可用以度量决策者对决策方案附属的收益或者损失的直接反应与感觉,是决策者自身价值观在决策过程中的综合体现,反映了决策者对待风险的态度。
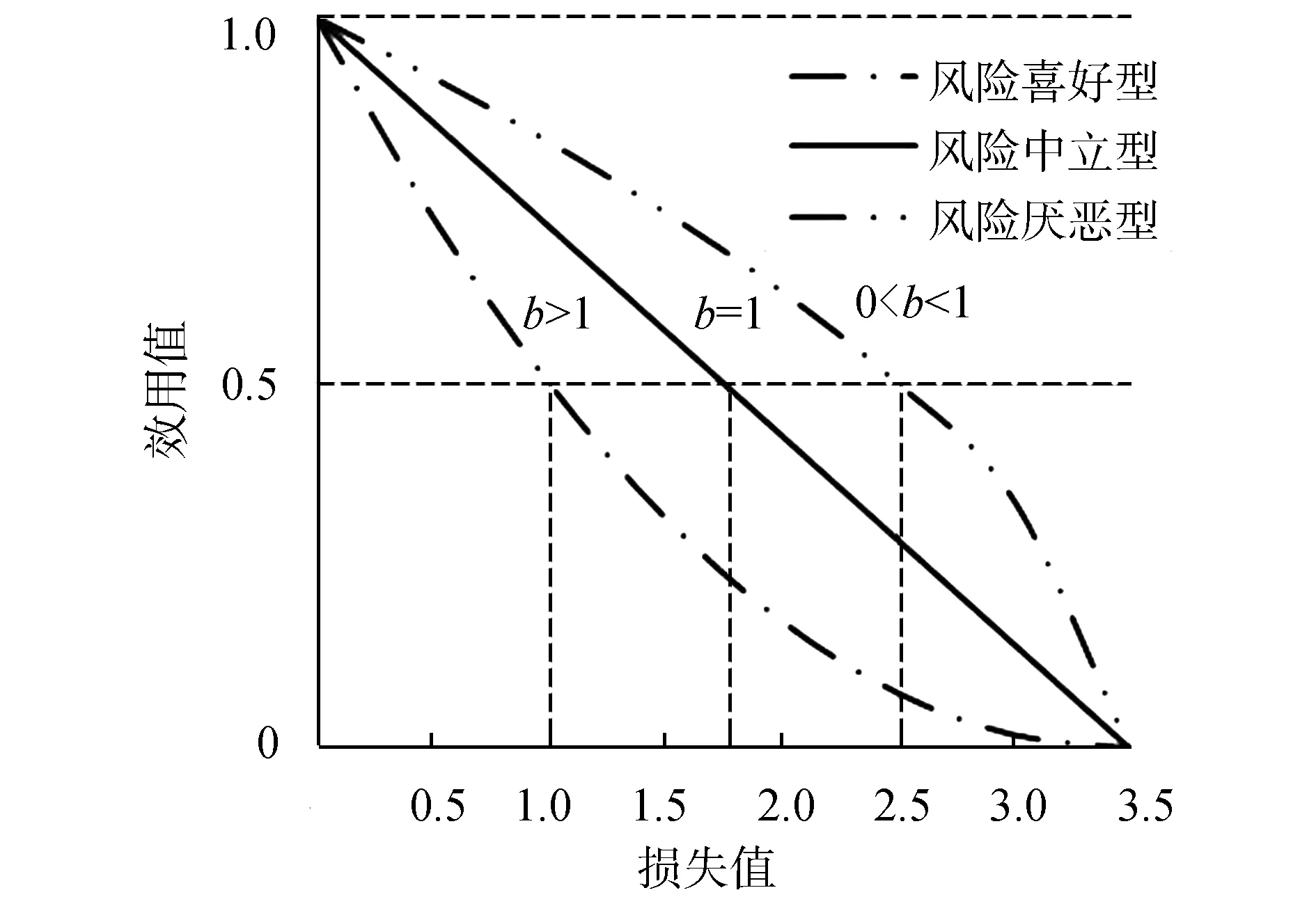
效用函数需满足相应公理体系,根据决策者关于风险的态度,效用函数可分为风险中立型、风险喜好型和风险厌恶型,如图1所示。从收益观点看,风险中立型效用曲线收益期望的最大效用与最大期望效用一致,对决策者而言无论是否有风险,都将选择期望收益最大的方案。风险厌恶型效用曲线,任一收益的效用都大于期望效用,表明决策者偏于保守,不愿意冒风险。风险喜好型效用曲线,任一收益的效用都低于期望效用,为了达到最大期望效用,决策过程中决策者将选择风险较大的方案。根据收益值与效用的关系,不同决策者将会选择避开风险,冒险还是仅参考客观期望值,从而影响最终决策结果。实际应用过程中,常采用混合型效用函数,如‘S’型效用函数。前期采用风险喜好型效用曲线,但当达到一定收益后,则采用保守策略。
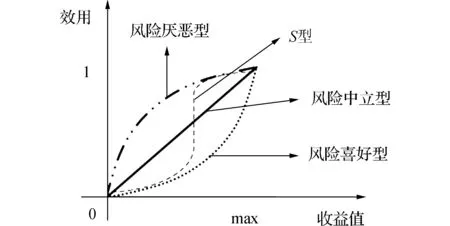
图1 效用函数曲线Fig.1 The utility function curves
2.2基于效用理论的三支决策模型
在三支决策粗糙集模型基础上,引入效用函数,即不同的决策动作会产生不同的效用。最大期望效用Bayesian决策过程与传统Bayesian风险决策过程最主要的区别是以效用函数代替损失函数,在决策过程中充分结合决策者自身关于风险的态度。效用函数以实际损失值(或收益值)为自变量,其值域区间可归约为[0,1]。当损失值为0时(或收益最大),此时效用最大,值为1;当损失达到最大值(或收益最低),此时效用最小,值为0,效用值将随着损失值增大而单调下降。
对于二值分类问题,三支决策粗糙集模型包含状态集Ω=U/D={X,Xc}(D为决策属性集),分别表示对象属于决策类X和不属于决策类X;3种关于X的决策方案为λ={aP,aB,aN},分别表示判定对象属于正域POSπ(X)、边界域BNDπ(X)和负域NEGπ(X)。不同状态变量下采取不同决策方案的效用如表1所示。

表1 效用函数
其中,λij(i=P,B,N,j=P,N)表示对象属于X、Xc状态下采取不同决策方案aP、aB和aN的损失值,u(λij)(i=P,B,N,j=P,N)表示损失值λij对应的效用值。u(λPP)、u(λBP)和u(λNP)分别表示在对象属于X的状态下采取决策方案aP、aB和aN时的效用值。u(λPN)、u(λBN)和u(λNN)分别表示在对象属于XC的状态下采取决策方案aP、aB和aN时的效用值。其中u(λPP)≥u(λBP)>u(λNP),表示在[x]⊆X状态下,将[x]判定为X正域的效用要大于将其判定为X边界域的效用,进一步大于将其判定为X负域的效用。u(λNN)≥u(λBN)>u(λPN),表示在[x]⊆XC状态下,将[x]判定为X负域的效用要大于将其判定为X边界域的效用,进一步大于将其判定为X正域的效用。
对于x∈U,[x]∈π采用3种决策方案aP、aB和aN的期望效用分别为
依据最大期望效用Bayesian决策准则,选择期望效用最大的决策方案作为最佳决策方案。效用三支决策模型的决策规则如下:
P) 若Ψ(aP|[x])≥Ψ(aB|[x])并且Ψ(aP|[x])≥ Ψ(aN|[x]),则判定[x]⊆POSπ(X);
B) 若Ψ(aB|[x])≥Ψ(aN|[x])并且Ψ(aB|[x])≥ Ψ(aP|[x]),则判定[x]⊆BNDπ(X);
N) 若Ψ(aN|[x])≥Ψ(aP|[x])并且Ψ(aN|[x])≥ Ψ(aB|[x]),则判定[x]⊆NEGπ(X)。
刘盾在文献[24]中对三支决策粗糙集中的阈值关系进行了相关研究。本文中,对于含有两种状态的决策系统,记P(X|[x])=P,则P(Xc|[x])=1-P。规则P)~N)可重写,具体推导过程如下:
对于规则P)的第1个条件,将期望效用公式代入,可转化为
同理,对于规则B)的第1个条件,将期望效用公式代入,可转化为
对于规则N)的第1个条件,将期望效用公式代入,可转化为
规则P)、B)和N)的第2个条件分别为上面推导的规则N)、P)和B)第1个条件的相反表示。规则P)、B)和N)的第2个条件可分别转化为
因此,依据效用3支决策模型的决策准则,规则P)~N)可简化为
P1) 若P(X|[x])≥αu并且P(X|[x])≥γu,则判定[x]⊆POSπ(X)
B1) 若P(X|[x])≥βu并且P(X|[x])≤αu,则判定[x]⊆BNDπ(X)
N1) 若P(X|[x])≤γu并且P(X|[x])≤βu,则判定[x]⊆NEGπ(X)其中αu、βu和γu分别为
由u(λPP)≥u(λBP)>u(λNP)和u(λNN)≥u(λBN)> u(λPN),则αu∈(0,1],βu∈[0,1),γu∈(0,1)。进一步通过变换可得:
若βu≠0,则有
Δ(αu)度量了在状态[x]⊆X下由边界域移动到正域效用增加值与在状态[x]⊆Xc下由边界域移动到正域效用减少值的比例;Δ(βu)度量了在状态[x]⊆X下由边界域移动到负域效用减少值,与在状态[x]⊆Xc下由边界域移动到负域效用增加值的比例;Δ(γu)度量了在状态[x]⊆X下由正域移动到负域效用减少值与在状态[x]⊆Xc下由正域移动到负域效用增加值的比例。Δ(αu)、Δ(βu)和Δ(γu)分别涉及两种状态下正域与边界域、边界域与负域和正域与负域间的转换。不同决策者对待风险的态度不同将导致获得的效用函数不同,从而在相同客观因素下得到的参数差异较大,影响最终的决策判定结果。
根据边界域规则(B1),设αu>βu,即
也就是说,当满足条件
得到0≤βu<γu<αu≤1。上式条件也可表示为Δ(αu)<Δ(βu),表示两种状态变量下正域与边界域间转换引起的效用值变化比例低于边界域与负域间转换引起的效用值变化比例。
当存在两种决策方案的期望效用同时达到最大,此时决策者将从两种方案中选其一。通过使用决胜规则,当P(X|[x])=αu时,划分到正域和边界域的期望效用同时达到最大,此时判定[x]⊆POSπ(X);当P(X|[x])=βu时,划分到边界域和负域的期望效用同时达到最大,此时判定[x]⊆NEGπ(X)。规则P1)~N1)可进一步化简为
P2) 若P(X|[x])≥αu,则[x]⊆POSπ(X)
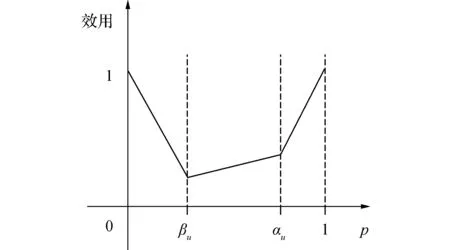
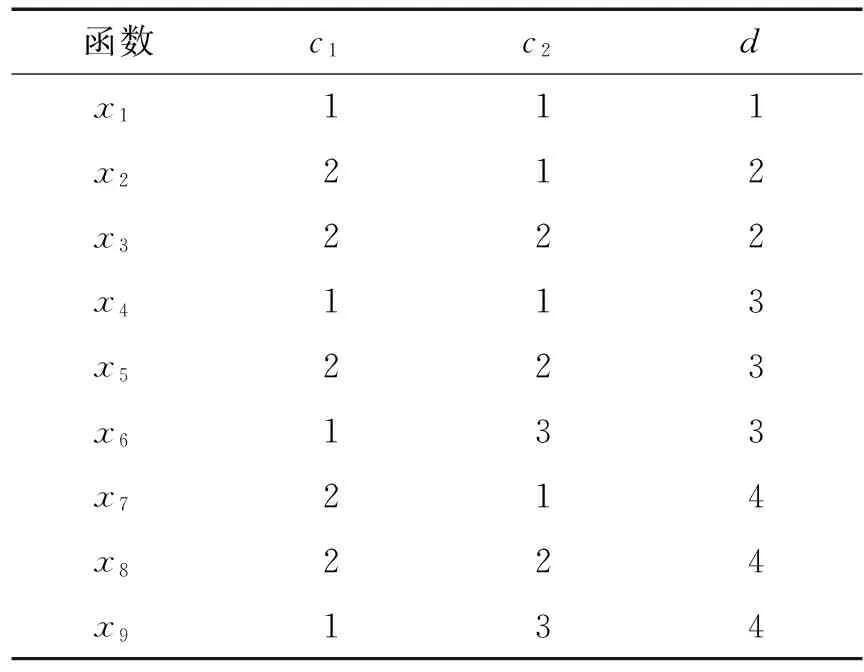
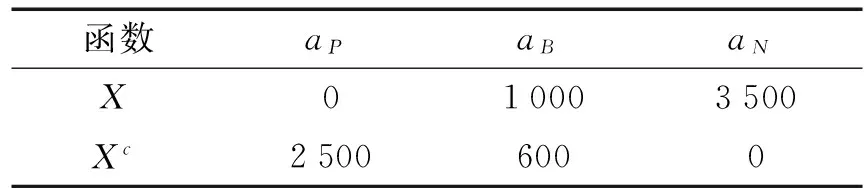
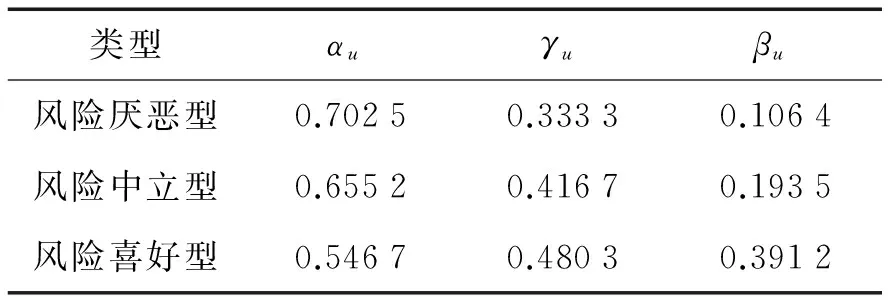
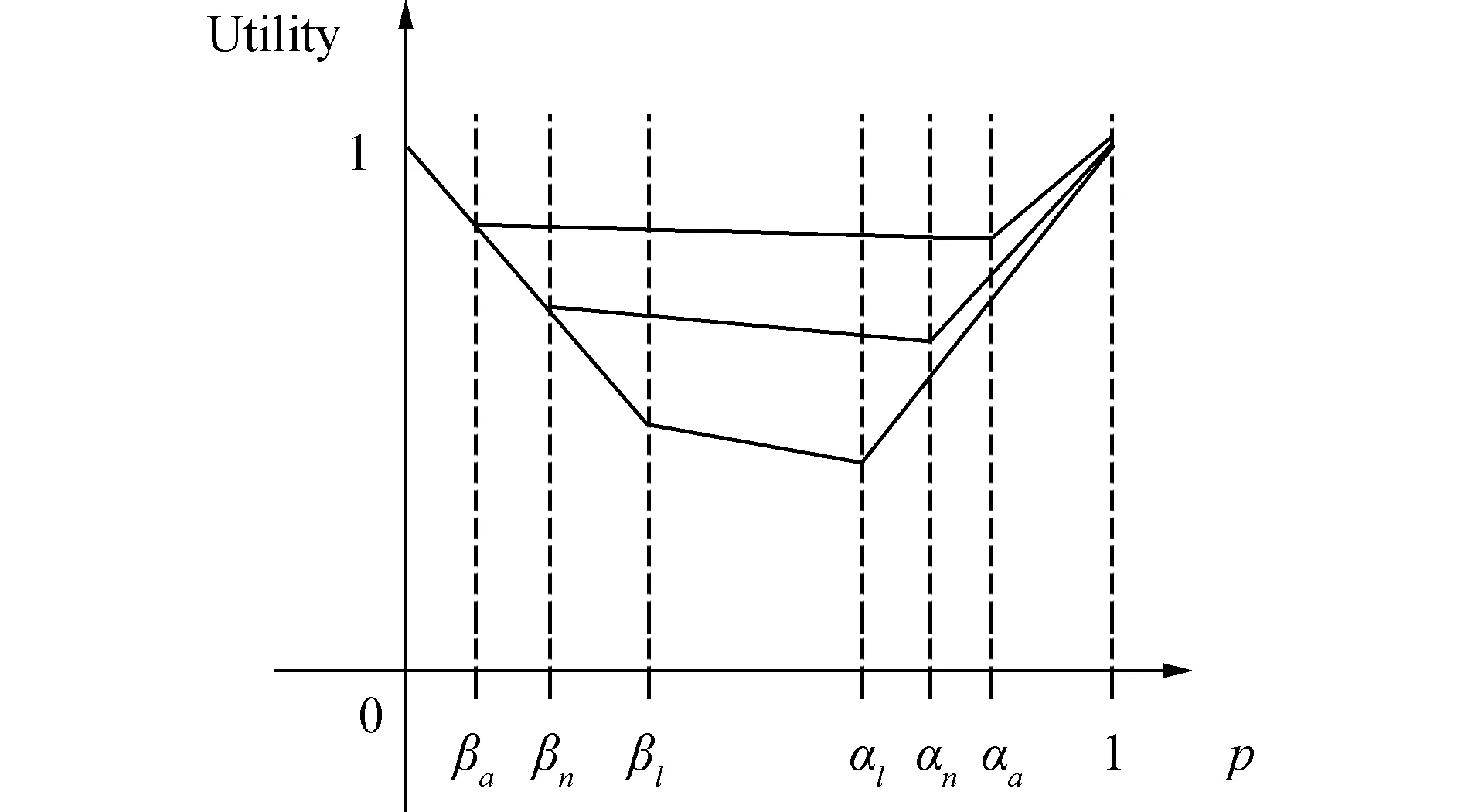
B2) 若βu N2) 若P(X|[x])≤βu,则[x]⊆NEGπ(X)在效用三支决策模型中,关于集合X⊆U的(αu,βu)-上、下近似可表示为 将单个对象划分到正域、边界域、负域分别会产生不同的效用。设p=P(X|[x]),对于任意属性集A⊆C,单个对象划分到X正域、边界域、负域的效用分别表示如下: 1) 单个对象划分到X正域的效用为 2) 单个对象划分到X边界域的效用为 3) 单个对象划分到X负域的效用为 亦即,若将对象x划分到正域,得到的效用等于其在状态[x]⊆X和[x]⊆Xc下划分到正域的效用与对应概率的乘积之和;若将对象x划分到边界域,得到的效用等于其在状态[x]⊆X和[x]⊆Xc下划分到边界域的效用与对应概率的乘积之和;若将对象x划分到负域,得到的效用等于其在状态[x]⊆X和[x]⊆Xc下划分到负域的效用与对应概率的乘积之和。 给定一个决策表,对于任意属性集A⊆C,有多个对象划分到正域、边界域和负域。正域效用、边界域效用、负域效用分别表示如下: 式中:xi表示划分到正域的对象,xj表示划分到边界域的对象,xk表示划分到负域的对象。正域效用等于划分到正域的所有对象的效用和。边界域效用等于划分到边界域的所有对象的效用和。负域效用等于划分到负域的所有对象的效用和。 UtilityA= 2.3效用与对象的概率之间的关系讨论 在效用三支决策模型中,假设做出正确决策的效用最大,即u(λPP)=u(λNN)=1。效用随着对象的概率变化会呈现3种情况,如图2所示。 图2 效用函数曲线Fig.2 The utility function curves 图2中横坐标表示对象的概率p,纵坐标表示决策的效用 Utility (p)。一对阈值(α u ,β u )将概率p的取值划分成3个区域[0,β u ]、(β u ,α u )和[α u ,1],分别对应对象划分到负域、边界域和正域。由对象的效用公式可知,每个区域中效用均随概率呈线性变化。无论β u /(1-α u )与γ u /(1-γ u )是何种关系,当p∈[0,β u ]时,效用随概率p的增加呈线性下降,说明判定为负规则的概率(1-p)越小,效用越小;当p∈[α u ,1]时,效用随概率p的增加呈线性上升,说明判定为正规则的概率p越大,效用越大。当p∈(β u ,α u )时,效用随概率p的增加呈现出3种不同的情况。即当判定为边界规则时,随概率的增加,效用可能是增加、不变或减少。此时,效用的变化趋势可通过判定β u /(1-α u )与γ u /(1-γ u )的关系获得。具体推导过程如下: 由于u(λNP)-1<0,所以当p∈[0,βu]时,效用随概率增加呈单调下降。 当p∈[αu,1]时, 由于1-u(λPN)>0,所以当p∈[αu,1]时,效用随概率增加呈单调上升。 当p∈(αu,βu)时,效用可能随概率增加呈单调上升、不变或下降。在p=αu,p=βu两点的效用分别采用划分到正域和负域的效用公式计算。在图2(a)中,满足以下条件 Utility(βu) 由于u(λNP)-1<0,1-αu>0,所以 对上式右侧进行变换得 所以可变换为 同理,在图2(b)中,Utility(βu)=Utility(αu),得 在图2、3中,Utility(βu)>Utility(αu),可得 可以看到,概率p的值靠近0和1时,效用增大,即确定性程度越大,效用越大;概率p的值靠近βu和αu时,效用减少,即不确定性程度越大,效用越小。 为了较好地描述效用三支决策模型的有效性,给定一个决策表(如表2)进行分析。该决策表的损失函数如表3所示。 表2 决策表 表3 损失函数 效用函数可采用Von Neumann-Morgenstern标准测定法,即通过询问打分的方式确定,但操作较为复杂,实际应用中常采用函数拟合等方法。常见的效用函数有指数效用函数u(x)=a+be-cx(c≥0)、对数效用函数u(x)=aln(x+b)+c(x+b>0)和二项式类型效用函数u(x)=a(x-1/2ax2)+b(ax≤1)等。本文通过L-A拟合法,即设效用函数曲线满足u(λ)=a(-λ+c)b,可得到如图3所示的3种效用曲线。其中u(0)=1,u(3 500)=0,风险厌恶型曲线令u(2 500)=0.5,风险喜好型曲线令u(1 000)=0.5,风险中立型曲线满足u((0+3 500)/2)=0.5。参数b决定效用曲线类型,其中0 图3 效用拟合函数曲线Fig.3 The utility fitting function curves 可以看到,风险中立型的曲线斜率为常数,表明决策者在每减少1单位的损失时所得到的满足感都相同,而且每增加1单位损失时的失望也相同。风险厌恶型的曲线斜率随损失值增加而增大,说明摆脱更多的损失带给决策者的满足程度比放弃好的效用带给决策者的失望程度大。风险喜好型的曲线斜率随损失值减少而增大,说明决策者更关心损失值较小时得到的满足感。经计算,3种效用拟合曲线下得到的效用函数如表4。由3种效用曲线下的效用函数计算得到的αu、γu和βu值如表5所示。 表4 3种模型下的效用函数 表5 效用拟合函数下得到的各参数值 分别通过属性{c1}、{c2}、{c1,c2}和{d}进行划分,结果如下: U/{c1}={{x1,x4,x6,x9},{x2,x3,x5,x7,x8}}, U/{c2}={{x1,x2,x4,x7},{x3,x5,x8},{x6,x9}}, U/{c1,c2}={{x1,x4},{x2,x7},{x3,x5,x8},{x6,x9}}, U/{d}={{x1},{x2,x3},{x4,x5,x6},{x7,x8,x9}}。 风险厌恶型中, 风险中立型中, 风险喜好型中, 经验证风险中立型效用曲线下得到的参数值与三支决策粗糙集模型下的结果一致。若决策者采用风险中立型效用曲线,则效用三支决策模型将退化为三支决策粗糙集模型,因为此时无论是否有风险,决策者都仅根据客观期望值进行决策,不加入任何自身的主观因素。进一步分析发现(0.106 4, 0.702 5)⊃(0.193 5,0.655 2)⊃(0.391 2,0.546 7),表示由风险厌恶型到风险喜好型,边界域将不断缩小,而正域和负域将扩大。这说明风险厌恶型效用曲线下,较少的对象被确定分类,而较多的对象划分到边界域中,决策偏于保守,为了进一步分类边界域中的对象,决策者需要获得更多信息或知识;风险喜好型效用曲线下,较多的对象被确定分类,而较少的对象包含于边界域中,决策偏于冒险,对于某些对象,即使在缺乏信息情况下,决策者亦敢于做出确定决策。 图4 效用和概率之间的关系Fig.4 The relationships between the utility and probability 由表5计算可得,风险厌恶型、风险中立型和风险喜好型3种模型都满足βi/(1-αi)<γi/(1-γi)(i=a,n,l)的关系(如图4所示),其中,风险厌恶型、风险中立型和风险喜好型的阈值分别为(βa,αa)、(βn,αn)和(βl,αl)。在这种情况下,风险厌恶型决策产生的效用≥风险中立型决策产生的效用≥风险喜好型决策产生的效用。因此,通过效用值的大小关系可以判断出决策者对待风险的不同态度。 本文将效用理论运用到三支决策粗糙集模型中,并将风险损失函数扩展为效用函数,提出了效用三支决策模型。结合文章的研究工作,有如下3点结论: 1)效用函数可以较合理的为决策主观能动性的量化提供度量标准; 2)决策的总效用为正域效用,负域效用与边界域效用之和; 3)决策的效用与概率之间存在区间性单调关系。接下来,如何结合效用函数特性,构建效用三支决策模型的合理属性约简目标函数将是下一步主要研究工作。 [1]LIU Dun, LIANG Decui, WANG Changchun. A novel three-way decision model based on incomplete information system[J]. Knowledge-based systems, 2016, 91: 32-45. [2]LIANG Decui, PEDRYCZ W, LIU Dun, et al. Three-way decisions based on decision-theoretic rough sets under linguistic assessment with the aid of group decision making[J]. Applied soft computing, 2015, 29: 256-269. [3]LIU Dun, LI Tianrui, ZHANG Junbo. Incremental updating approximations in probabilistic rough sets under the variation of attributes[J]. Knowledge-based systems, 2015, 73: 81-96. [4]MIN Fan, HE Huaping, QIAN Yuhua, et al. Test-cost-sensitive attribute reduction[J]. Information sciences, 2011, 181(22): 4928-4942. [5]ZHANG Hengru, MIN Fan. Three-way recommender systems based on random forests[J]. Knowledge-based systems, 2016, 91: 275-286. [6]DENG Xiaofei, YAO Yiyu. Decision-theoretic three-way approximations of fuzzy sets[J]. Information sciences, 2014, 279: 702-715. [7]DENG Xiaofei, YAO Yiyu. A multifaceted analysis of probabilistic three-way decisions[J]. Fundamenta informaticae, 2014, 132(3): 291-313. [8]YAO Yiyu. Three-way decisions with probabilistic rough sets[J]. Information sciences, 2010, 180(3): 341-353. [9]ZHANG Xianyong, MIAO Duoqian. Reduction target structure-based hierarchical attribute reduction for two-category decision-theoretic rough sets[J]. Information sciences, 2014, 277: 755-776. [10]HERBERT J P, YAO Jingtao. Game-theoretic rough sets[J]. Fundamenta informaticae, 2011, 108(3/4): 267-286. [11]ZHOU Bing, YAO Yiyu, LUO Jigang. Cost-sensitive three-way email spam filtering[J]. Journal of intelligent information systems, 2014, 42(1): 19-45. [12]HU Baoqing. Three-way decision spaces based on partially ordered sets and three-way decisions based on hesitant fuzzy sets[J]. Knowledge-based systems, 2016, 91: 16-31. [13]李华雄, 周献中, 李天瑞, 等. 决策粗糙集理论及其研究进展[M]. 北京: 科学出版社, 2011. [14]贾修一, 商琳, 周献中, 等. 三支决策理论与应用[M]. 南京: 南京大学出版社, 2012. [15]YANG Xiaoping, YAO Jingtao. Modelling multi-agent three-way decisions with decision-theoretic rough sets[J]. Fundamenta informaticae, 2012, 115(2/3): 157-171. [16]MA Xi’ao, WANG Guoyin, YU Hong, et al. Decision region distribution preservation reduction in decision-theoretic rough set model[J]. Information sciences, 2014, 278: 614-640. [17]YU Hong, LIU Zhanguo, WANG Guoyin. An automatic method to determine the number of clusters using decision-theoretic rough set[J]. International journal of approximate reasoning, 2014, 55(1): 101-115. [18]贾修一, 李伟湋, 商琳, 等. 一种自适应求三枝决策中决策阈值的算法[J]. 电子学报, 2011, 39(11): 2520-2525. JIA Xiuyi, LI Weiwei, SHANG Lin, et al. An adaptive learning parameters algorithm in three-way decision-theoretic rough set model[J]. Acta electronica sinica, 2011, 39(11): 2520-2525. [19]LIU Dun, LI Tianrui, LIANG Decui. Incorporating logistic regression to decision-theoretic rough sets for classifications[J]. International journal of approximate reasoning, 2014, 55(1): 197-210. [20]刘盾, 李天瑞, 苗夺谦, 等. 三支决策与粒计算[M]. 北京: 科学出版社, 2013. [21]YAO Yiyu, WONG S K M, LINGRAS P. A decision-theoretic rough set model[C]//RAS Z W, ZEMANKOVA M, EMRICH M L. Methodologies for Intelligent Systems, Vol. 5. New York: North-Holland, 1990: 17-24. [22]YU Hong, CHU Shuangshuang, YANG Dachun. Autonomous knowledge-oriented clustering using decision-theoretic rough set theory[J]. Fundamenta informaticae, 2012, 115(2/3): 141-156. [23]贾修一, 商琳, 周献中, 等. 三支决策理论与应用[M]. 南京: 南京大学出版社, 2012: 17-33. [24]刘盾, 李天瑞, 李华雄. 粗糙集理论: 基于三支决策视角[J]. 南京大学学报: 自然科学版, 2013, 49(5): 574-581. LIU Dun, LI Tianrui, LI Huaxiong. Rough set theory: a three-way decisions perspective[J]. Journal of Nanjing university: natural sciences, 2013, 49(5): 574-581. [25]JIA Xiuyi, LIAO Wenhe, TANG Zhenmin, et al. Minimum cost attribute reduction in decision-theoretic rough set models[J]. Information sciences, 2013, 219: 151-167. [26]LI Huaxiong, ZHANG Libo, HUANG Bing, et al. Sequential three-way decision and granulation for cost-sensitive face recognition[J]. Knowledge-based systems, 2016, 91: 241-251. [27]QIAN Yuhua, ZHANG Hu, SANG Yanli, et al. Multigranulation decision-theoretic rough sets[J]. International journal of approximate reasoning, 2014, 55(1): 225-237. [28]DOU Huili, YANG Xibei, SONG Xiaoning, et al. Decision-theoretic rough set: a multicost strategy[J]. Knowledge-based systems, 2016, 91: 71-83. [29]于洪, 王国胤, 姚一豫. 决策粗糙集理论研究现状与展望[J]. 计算机学报, 2015, 38(8): 1628-1639. YU Hong, WANG Guoyin, YAO Yiyu. Current research and future perspectives on decision-theoretic rough sets[J]. Chinese journal of computers, 2015, 38(8): 1628-1639. [30]于洪, 王国胤, 李天瑞, 等. 三支决策: 复杂问题求解方法与实践[M]. 北京: 科学出版社, 2015: 300-313. [31]李华, 胡奇英. 预测与决策教程[M]. 北京: 机械工业出版社, 2012. 张楠,男,1979年生,讲师,博士,主要研究方向为粗糙集、认知信息学与人工智能。 姜丽丽,女,1990年生,硕士研究生,主要研究方向为粗糙集理论、粒计算。 Utility-based three-way decisions model ZHANG Nan1, JIANG Lili1, YUE Xiaodong2, ZHOU Jie3 (1. School of Computer and Control Engineering, Yantai University, Yantai 264005, China; 2. School of Computer Engineering and Science, Shanghai University, Shanghai 200444, China; 3. Research and Development Center of Lugu Industrial Park, Zoomlion Heavy Industry Science & Technology Development Co., Ltd., Changsha 410205, China) Risk decisions are usually influenced by subjective and objective factors. During the process of decision-making, decisions are based not only on the objective risk but also on the subjective activity of decision-makers. In order to introduce decision-makers’ subjective attitudes to risk, a model of utility-based three-way decisions (UTWD) was produced by extending the risk function to a utility function. The monotonic relationships between the utility and probabilities of objects in three regions were investigated systematically. The computational methods for positive region utility, boundary region utility, and negative region utility are also given. Finally, an example is given to substantiate the conceptual arguments. The model is an extension of three-way decisions and provides a beneficial investigation into subjective risk measures in three-way decision research. utility theory; three-way decisions; rough sets; artificial intelligence; risk decisions 10.11992/tis.201606010 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.TP.20160808.0831.028.html 2016-06-03. 网络出版日期:2016-08-08. 国家自然科学基金项目(61403329, 61572418, 61502410, 61572419, 61573235);山东省自然科学基金项目(ZR2013FQ020, ZR2015PF010, ZR2013FM011);山东省高等学校科技计划项目(J15LN09). 姜丽丽. E-mail:ytjianglili0919@163.com. TP181 A 1673-4785(2016)04-0459-10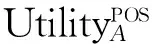
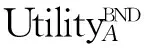
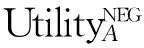


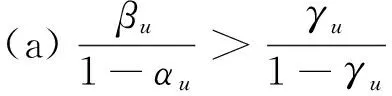
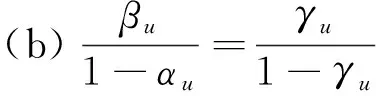
3 实例分析

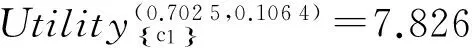
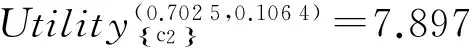
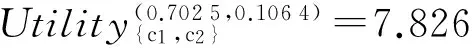
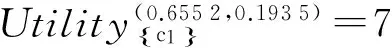
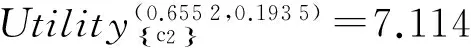
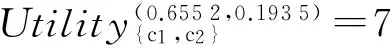
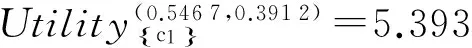
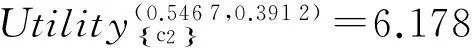
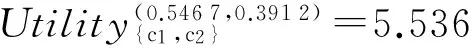
4 结论


