基于傅里叶级数的多环反馈开关电流小波滤波器实现

李目，吴笑锋，席在芳，何怡刚



基于傅里叶级数的多环反馈开关电流小波滤波器实现

李目1，吴笑锋1，席在芳1，何怡刚2

(1. 湖南科技大学 信息与电气工程学院，湖南 湘潭，411201；2. 合肥工业大学 电气与自动化工程学院，安徽 合肥，230009)

提出一种基于傅里叶级数的多环反馈结构开关电流小波滤波器设计新方法。利用傅里叶级数法求取小波函数的时域小波逼近函数，以双输入多输出开关电流双线性积分器和单输入多输出电流镜作为基本单元设计相应的多环反馈结构小波滤波器，并通过调节开关电流滤波器的时钟频率获得不同尺度小波函数。对所设计的电路进行时域、频域和灵敏度分析，并研究元件非理想性对电路的影响。研究结果表明：该方法的小波逼近函数求取容易，滤波器电路具有设计简单、灵敏度低和受非理想性因素影响小的特点。

小波函数；傅里叶级数；函数逼近；开关电流滤波器；多环反馈结构

小波变换作为一种良好的时频分析工具被广泛地应用于工程领域的信号处理，它是分析非平稳随机时变信号最有效的数学工具之一。由于传统的连续小波变换通常采用数字电路结合软件实现，难以满足低压、低功耗、实时和微型化的应用要求，因此，连续小波变换的模拟电路的实现成为国内外模拟信号处理领域研究的热点。目前，采用模拟电路实现连续小波变换方法主要有时域法和频域法。时域法是根据连续小波变换定义设计小波函数发生器、乘法器和积分器实现。由于设计产生不同尺度和位移小波簇的小波函数发生器难度很大，所以，采用时域法实现连续小波变换的研究进展缓慢，频域法成为当前的主要方法。在频域上，连续小波变换可看成是不同尺度且品质因数恒定的带通滤波器组对信号进行滤波处理，因此，设计多尺度的小波滤波器成为模拟硬件实现连续小波变换的关键技术。迄今为止，国内外学者提出了多种模拟滤波器实现连续小波变换的方法。其中，滤波器的类型主要包括连续时间滤波器[1−9]和抽样数据滤波 器[10−15]。由于抽样数据滤波器的时间常数可通过调节时钟频率或元件参数比来达到精确控制，滤波器的频率特性容易改变，因此，采用抽样数据滤波器电路实现连续小波变换方法得到了研究者们的广泛关注。例如，LIN等[10]提出了基于并联结构开关电容滤波器的连续小波变换实现方法，通过调节滤波器中的时钟频率精确实现不同尺度小波函数，但开关电容电路中需要线性浮置电容，该结构与数字VLSI CMOS工艺不兼容，难于集成化。此外，随着集成工艺的发展，电源电压越来越低，直接减小电路上的最大电压摆幅，致使电压模开关电容电路的动态范围会随之减小，特别是低压高速的运算放大器设计困难。为了解决开关电容电路面临的问题，基于电流模开关电流技术的小波滤波器实现成为当前的重要研究方向。其中，胡沁春等[11]提出了基于Padé频域逼近的串联结构开关电流滤波器实现连续小波变换方法，但Padé逼近法中分子和分母多项式次数难于确定且不能保证获得的系统是稳定的。赵文山等[12]利用最小二乘法逼近时域小波函数，采用并联结构开关电流滤波器设计实现连续小波变换，但最小二乘法属于局部优化算法，使该算法收敛至最优的初始值难以选择；LI等[13−15]采用智能优化算法逼近时域小波函数，但该算法的参数设置复杂，迭代次数多，运行时间长。另外，串、并联结构小波滤波器电路较复杂，且通带灵敏度高。针对上述方法的不足，本文作者提出一种基于傅里叶级数的多环反馈开关电流小波滤波器设计新方法。利用傅里叶级数逼近法求取时域小波逼近函数，并采用开关电流双线性积分器和电流镜电路作为基本单元设计出冲激响应为小波逼近函数的多环反馈小波滤波器，通过调节滤波器的时钟频率获得不同尺度小波函数。通过仿真实验结果验证该方法的有效性。

1 小波函数的傅里叶级数逼近

傅里叶级数逼近属于一种正交函数逼近法。周期函数()的傅氏级数展开式为

其中：a为()的傅氏级数展开的系数。由式(1)可知：()为周期函数，用它无法直接逼近1个可实现的时限脉冲响应函数()(如小波函数)。为了能够应用傅里叶级数逼近该类型函数，可沿时间轴重复()产生1个周期为的周期信号h()，且将式(1)中无限项截断成只包含2+1项的傅氏级数展开式及频域表达式：

为了保留h()在0＜＜时的部分，将h()∙()经过1个差分系统[16]：

则

式中：“*”表示卷积。由式(4)可知：该函数不是有理函数，不能直接通过电路综合实现。为了利用傅氏级数逼近算法，对被研究函数进行处理。假设()为时限函数，即对于＜0和＞，构造2个周期函数h1()和h2()：

且

根据函数h1()和h2()的对称性，在2周期内将它们展开成傅里叶级数，h1()只包含奇次谐波，h2()只包含偶次谐波。现构造函数和，分别定义为

将式(7)代入式(8)并整理后得

将式(7)和式(9)代入式(4)可求得()为

()经拉普拉斯反变换后即可获得()。

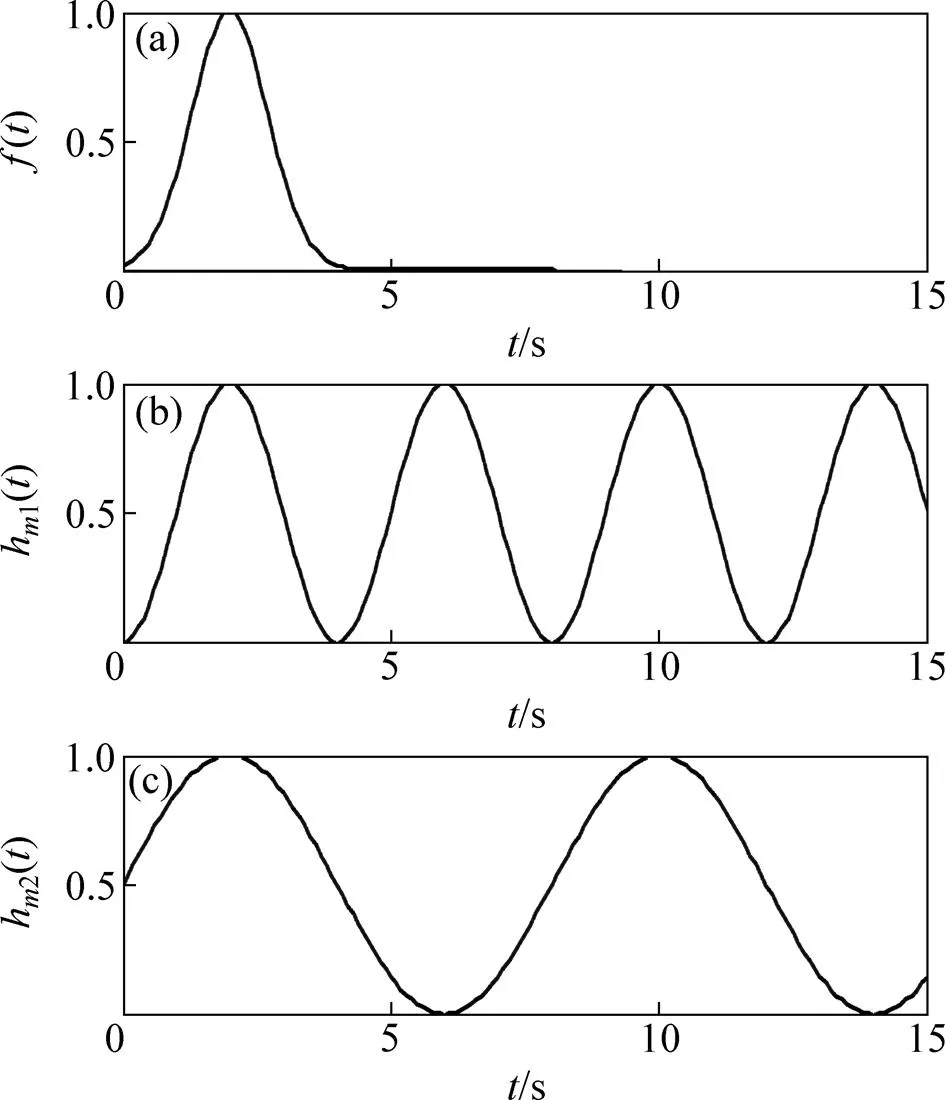
()，h1()和h2()的波形如图1所示。