基于线性函数型权重的RBF−ARX模型的磁悬浮球系统预测控制

覃业梅，彭辉，阮文杰



基于线性函数型权重的RBF−ARX模型的磁悬浮球系统预测控制

覃业梅1, 2, 3，彭辉1, 3, 4，阮文杰1, 3

(1. 中南大学 信息科学与工程学院，湖南 长沙，410083；2. 湖南商学院 计算机与信息工程学院，湖南 长沙，410205；3. 先进控制与智能自动化湖南省工程实验室，湖南 长沙，410083；4. 两型社会与生态文明协同创新中心，湖南 长沙，410083)

为了充分描述磁悬浮球系统具有非线性、开环不稳定性及响应快速性等特性，建立一个带线性函数权重的RBF-ARX(linear functional weight RBF networks-based ARX model, LFWRBF−ARX)模型。与一般的RBF−ARX模型不同之处在于，它引入1个与工作点状态相关的局部线性结构作为RBF网络输出层的权值。该模型随系统工作点的变化而变化，固定工作点时为局部线性ARX模型，当工作点变化时为全局非线性ARX模型。根据该模型的结构特点，采用结构化非线性参数优化方法(structured nonlinear parameter optimization method, SNPOM)来辨识模型的结构及线性、非线性参数。然后，以辨识的模型为基础，根据模型的局部线性及全局非线性特征设计预测控制器。仿真结果表明：以该建模方法建立的模型能很好地局部和全局描述磁悬浮球系统的动态特性，并能实现小球的稳定悬浮控制，比以一般ARX模型、RBF−ARX模型为基础的控制效果更好。

非线性ARX模型(NARX)；线性函数权重RBF−ARX模型(LFWRBF−ARX)；SNPOM(structured nonlinear parameter optimization method)；非线性预测控制；磁悬浮球

磁悬浮技术因其无接触、低噪声及摩擦小等特点已广泛应用于磁悬浮列车、磁悬浮轴承等工程领域。磁悬浮小球系统是一个复杂的非线性、开环不稳定的系统，易受电源及外界环境的影响，某些参数具有较强的不确定性，无法精确测量，常作为实验室研究平台。近年来，对磁悬浮装置的控制研究已取得了很多成果，如将非线性模型进行线性化处理后对磁悬浮系统采用线性控制方法[1−2]，应用反馈线性化或前馈线性化技术设计非线性控制器。此外，还有研究者应用PID结合其他方法[3]或广义PID[4]来提高磁悬浮控制的鲁棒性，扩大稳定控制的范围。自适应控制[5]、变结构或滑膜控制[6]、鲁棒控制[7]、神经网络控制[8]等非线性控制方法也被用于磁悬浮系统。在实际工业过程中，一种被广泛应用的先进控制方法是预测控制，它是20世纪70年代直接从工业过程中诞生的一类基于预测模型的先进控制算法。基于线性模型的预测控制已经在实际工业过程中得到广泛应用[9−10]，而基于非线性模型的预测控制(NMPC)[11]通过不断改进也逐步用于实践。KEMIH等[12]在1个线性化的磁悬浮模型基础上运用带约束的广义预测控制(GPC)来保证系统的稳定控制。WANG等[13]采用网络反馈线性化预测控制来补偿网络延时的影响。为了提高计算效率和改善实时控制性能，ULBIG等[1]建立了1个磁悬浮系统的分段仿射的线性模型，并提出1种显式NMPC策略。BACHLE等[14]通过将磁悬浮球系统非线性模型求导后实施梯度优化方法来提高稳定性和计算速度。实现预测控制的一个重要环节是建立系统的模型[15]，这是实现和提高其预测控制效果的重要环节。上述研究成果大多是以磁悬浮球系统的物理模型为基础得到的。由于系统的复杂性，其物理模型和某些参数难以得到，或在一些假定条件下近似获得。而由于预测控制算法不需要深入了解被控对象的内部机理以及对模型结构要求的不唯一性，使得它可以根据工业过程的特点和控制要求，根据系统的输入输出信息建立预测控制的内部模型。这一特点使得预测控制在实际工业过程中有了更广泛的应用空间。彭辉等[16]提出在不同平衡点对磁悬浮小球建立多个线性ARX模型，实现了多模型线性预测控制，但为了实现大范围的稳定控制，需要建立一组这样的模型，同时对切换机制也提出了较高要求。QIN等[17]在工作范围内建立1个全局非线性的RBF−ARX模型，实现了磁悬浮球的非线性预测控制，获得了较好的控制效果。本文作者在此基础上提出1种改进模型，用1个具有状态回归的局部线性权函数逼近一般RBF−ARX模型中的常数系数，进一步提高模型的局部线性及全局非线性的描述能力，以便更全面地刻画磁悬浮球系统的非线性动态特性。

1 带线性函数权重的RBF−ARX模型

根据输入输出数据驱动建立系统的模型是一种常用且实用的方法，如用带外部输入的自回归(ARX)模型可以很精确地描述线性系统。但对于一般的非线性系统，它的描述能力很弱，只能在局部小范围内对非线性系统的局部动态特性进行刻画，这使复杂系统基于此模型实施全局有效控制难度很大。为了更好地描述非线性系统的动态特性，将线性ARX模型扩展成非线性ARX模型，即1个非线性系统可用如下一般NARX表示：

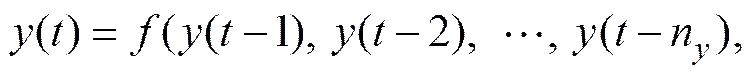
图1 带线性函数权值的RBF网络结构

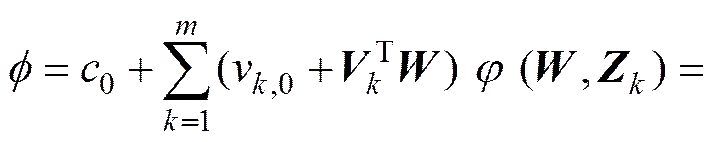
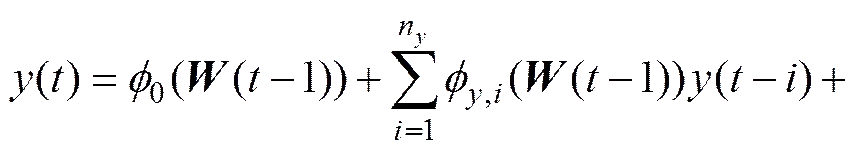
其中：()为系统输出量；()为系统输入量；表示2−范数；n和n分别为输出()和输入()的阶次。式(3)中的(−1)是时变的系统工作点状态，可以是输入信号、输出信号或系统的其他可测信号及其组合。该模型具有ARX的回归结构，对RBF网络中心的要求较宽松，即使所有的RBF网络共用同一个中心，回归系数也会不同，因而RBF网络需要的节点数目很少，而且该结构中回归权函数v也由系统的工作点状态(−1)决定，可能使RBF网络需要的节点数目更少。当(−1)确定后，式(3)就是1个简单的线性ARX模型，因此，能反映系统的局部线性特征。而从整体来看，由于工作点状态(−1)是不断变化的，故模型(3)也显示了全局的非线性特性。这种方法在某些神经网络系统中表现出很好的性能[22]，而且这样处理后的结构可以大大减少网络及其中心的数目，减少计算时间，为快速系统实施基于模型的预测控制奠定了基础。

2 磁悬浮球系统的建模与辨识

本文的研究对象是本实验室的1套磁悬浮小球控制系统。该套装置主要包括2部分，即由磁悬浮本体和控制该装置的1台计算机组成。磁悬浮小球控制装置的本体如图2所示。电磁铁、电源功放模块、光电传感器、LED光源和被控钢球等元件共同组成了磁悬浮小球控制装置的本体。小球质量为 22 g，直径为 12.5 mm，运动范围为 0~18 mm。该实验装置是1个典型的吸附式单自由度的磁悬浮控制系统，只能控制被控对象的上、下移动，为单输入单输出系统。电磁铁下表面为原点，竖直向下的方向为轴负方向，电磁铁与小球间的空隙为位移。控制目标是使钢球稳定悬浮在指定的位置或跟踪给定轨迹。一般地，基于磁悬浮机理建立的模型是在一定假设条件下建立的近似模型，存在较大非线性误差。为了提高非线性逼近能力，本文按前面提出的建模方法构建磁悬浮小球系统的线性权函数RBF−ARX模型(LFWRBF−ARX)。模型具体结构与式(3)所示的相同，电磁铁的控制电压为输入控制变量()，钢球向下的位移为输出变量()，将输出序列作为工作点的状态，即(−1)=[(−1)，…，(−n)]T。

图2 磁悬浮实验平台

LFWRBF−ARX模型的辨识主要包括模型的结构及参数辨识，模型的结构主要取决于各变量的阶次即n，n，和n。从式(3)可看出，该模型的参数含有线性参数和非线性参数。这类模型可应用PENG等[23]针对神经网络类模型提出的结构化非线性参数优化方法(SNPOM)。该方法根据模型结构特点，将模型参数分为线性参数和非线性参数，用Levenberg− Marquardt方法(LMM)来优化非线性参数，用最小二乘法(LSM)优化线性参数，优化过程以非线性参数循环优化为中心，交叉优化线性参数。这种方法不同于非结构化的一般梯度搜索方法，搜索最优解的过程更加灵活、快速、有效，尤其对于线性参数较多的系统，而且它是一种离线辨识方法。模型(3)包括非线性参数和、线性参数0和，因此，模型(3)共有(1+(n+1))(n+n+1)个线性参数和(+×n)个非线性参数待估计，线性参数远多于非线性参数，故本文采用该优化方法。模型的阶次估计以Akaike信息准则(AIC值)最小为衡量标准，同时综合考虑阶跃响应的动态特性。

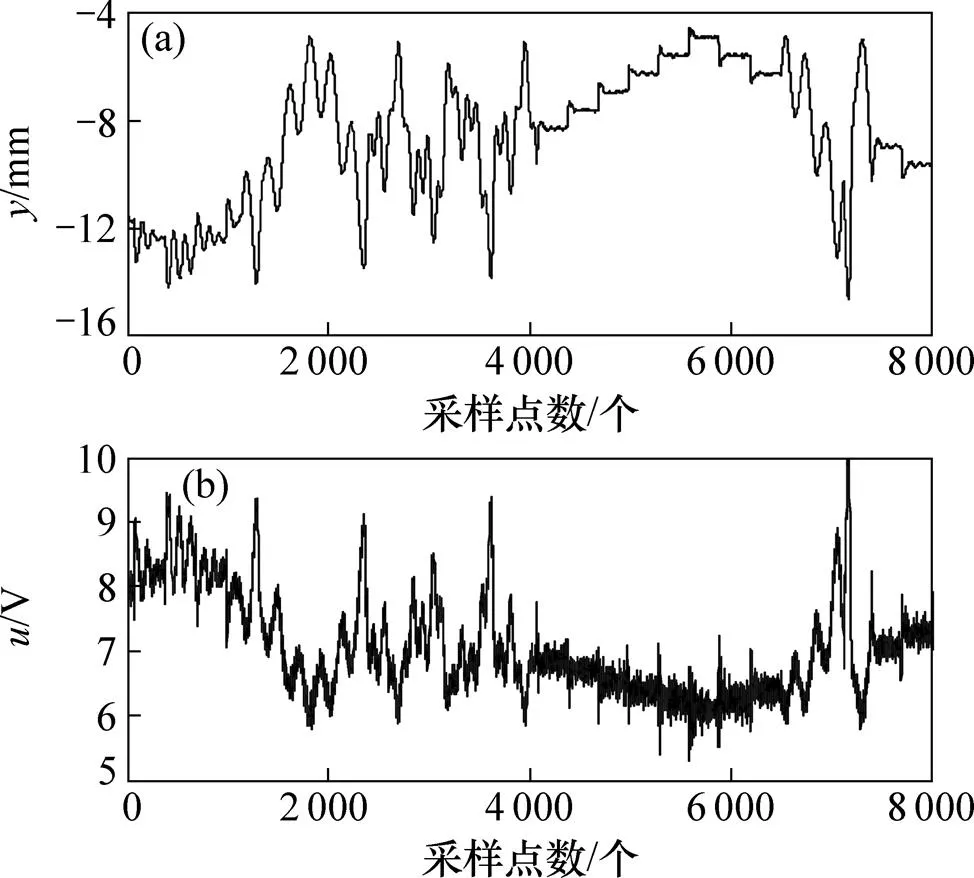
针对该磁悬浮小球系统，在MATLAB/ SIMULINK2010b工作环境下，在PID控制策略下用PCI1711数据采集卡采集钢球位移、电磁铁控制电压，采样周期为5 ms。为了使系统可辨识，要求小球尽可能在较大范围内稳定悬浮，同时在系统的输入端加入白噪声信号以便更好地激发其动态模式。应用PID控制策略采集的观测数据共取8 000个(如图3所示)，其中前4 000个数据用于优化模型阶次和参数，后4 000个数据用于测试所估计的模型性能。从图3可看出：该组数据设置钢球跟踪1个变化多样的信号，尽可能地激发系统的各种模态，便于辨识、估计得到与实际系统更逼近的模型。利用这些观测值，应用SNPOM方法估计LFWRBF−ARX模型参数，综合考虑AIC值及阶跃动态特性的原则反复训练和比较，得到模型阶次为n=5，n=3，=1和n=1，训练和测试结果如图4和图5所示。