有限元分析技术概述及优化实例

陈　曦，张　彪

（1.北京理工大学机电工程学院，北京 100081；2.广西大学机械工程学院，广西 南宁530004）

有限元分析技术概述及优化实例

陈曦1，张彪2

（1.北京理工大学机电工程学院，北京 100081；2.广西大学机械工程学院，广西 南宁530004）

该文介绍了有限元分析技术在工程中的应用以及利用有限元优化软件ANSYS的优化设计方法，针对小型甘蔗收获机刀盘齿轮箱箱体轻量化设计的问题，分别利用零阶法和一阶法对箱体结构进行优化计算，从而计算出最优解，即箱体前后板厚为5 mm、左右板厚为5 mm、底板厚度为20 mm，为小型甘蔗收获机整机的轻量化设计提供参考。

有限元；ANSYS；甘蔗收获机；齿轮箱

在工程领域，由于微分方程组的复杂性，以及难以确定的边界条件和初始条件，很难求得微分方程组的精确解。因此，需要借助有限差分法、有限元法等数值方法来求近似解［1］。本文利用有限元优化软件ANSYS的优化设计方法，针对小型甘蔗收获机刀盘齿轮箱箱体轻量化设计的问题，利用零阶法和一阶法对箱体结构进行优化计算，从而计算出最优解。

1　有限元分析技术

有限元法（Finite Element Method）是一种在工程分析领域应用广泛的数值计算方法。这种方法最先是用来求解航空工程结构中力与位移的关系，如果采样传统方法去求解微分方程，很难得到解析解。有限元法可以微分方程离散化，通过计算机编制程序辅助求解，大大提升了求解的精度和效率。有限元法的基本思想是将具有无限个自由度的连续的求解区域离散为具有有限个自由度、且按一定方式（节点）相互连接在一起的离散体（单元），即将连续体假想划分为数目有限的离散单元，而单元之间只在数目有限的指定点处相互联结，用离散单元的集合体代替原来的连续体。一般情况下，有限元方程是一组以节点位移为未知量的线性方程组，解次方程组可得到连续体上有限个节点上的位移，进而可求得各单元上的应力分布规律，尤其适用于应力分析、变形计算、疲劳计算、优化设计等，能够达到减轻构件重量和节省成本的目的［2］。

2　有限元优化软件ANSYS

ANSYS优化模块是通过FORTRAN语言将优化设计理论计算机化，实现面向对象的可视化界面，其主要提供了3种优化方法或工具：零阶法、一阶法和等步长搜索法［3］。每一种方法都是一系列分析—评估—修正的循环过程，直至所有的设计结果都满足要求。优化过程框图如图1所示。

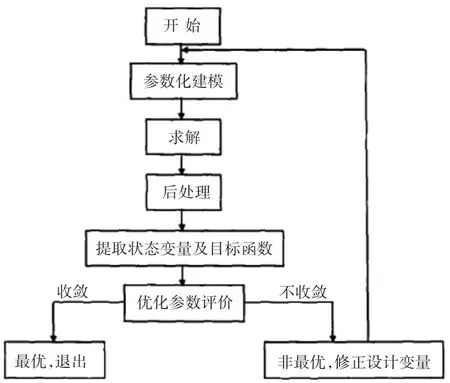
图1　ANSYS优化过程

在ANSYS优化设计中有三种变量，分别为设计变量、状态变量和目标函数。设计变量即自变量；状态变量用于定义优化的边界条件；目标函数是最终的优化目的，获得目标变量最小值。其中，设计变量和目标函数的公差用于控制优化过程的收敛性，如果前后两次设计变量之间的误差小于其公差的话，优化过程自动停止。

3　小型甘蔗收获机刀盘齿轮箱箱体的优化设计

按照机械设计手册提供的设计方法，设计的小型甘蔗收获机刀盘齿轮箱的箱体如图2所示。箱体的壁厚在15 mm左右，箱体所承受的载荷主要来自箱体的自重，刀盘刀轴装配体的总重，轴承对箱体的挤压，土壤的作用反力传递到箱体上引起的载荷以及砍蔗过程等引起的冲击。

图2　箱体的主要结构尺寸

使用有限元方法先对设计的箱体进行分析，如果强度或刚度不能满足使用要求，则采取措施修改方案；若存在过大剩余，则对其结构进行优化设计，在保证满足使用要求的前提下力求总重量最小。

由于箱体铸造采用的灰铸铁HT150为脆性材料，其失效形式主要是受拉断裂，宜采用第一强度理论效核其强度。HT150所能承受的最大拉应力为150 MPa，在设计过程通常取3～5甚至更大的安全系数，将安全系数至少取为5，可得许用应力。利用ANSYS对箱体进行应力分析，从图3可知，最大应力值为18.6 MPa，箱体存在着较大的优化空间。

图3　箱体应力分布

对箱体的优化设计中，设计变量为箱体前后板厚（x1=thick_F_B）、左右板厚（x2=thick_L_R）和底板的厚度（x3=thick_B）；目标函数为箱体的总重；约束条件为箱体第一强度理论应力值不大于30 MPa.

利用零阶法对箱体结构进行优化计算，迭代结果如图4和图5所示。

图4　零阶法迭代结果

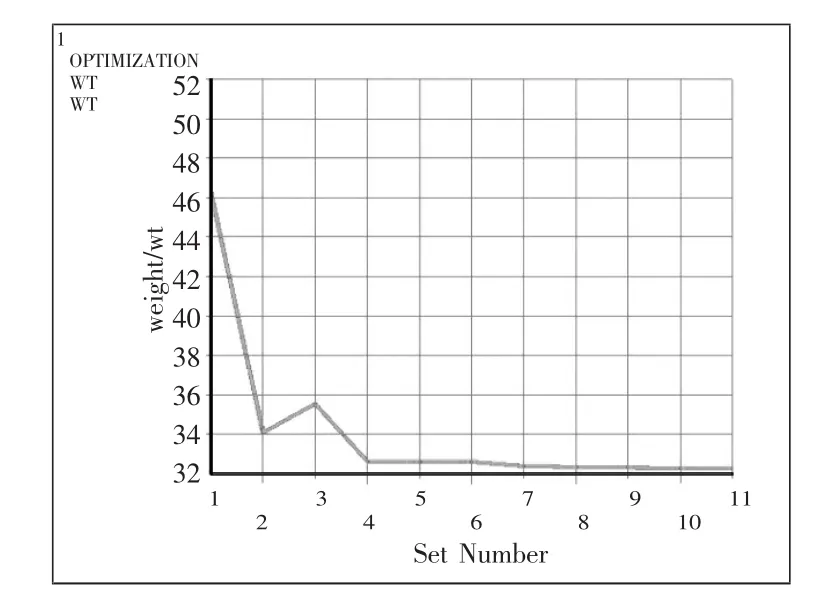
图5　零阶法目标函数迭代结果

由于零阶法是采用空间取点，然后再用曲面拟合，最后再求曲面极值的方法实现寻优过程的，所以它不能保证每次迭代都能得到可行解，也不能保证后一次迭代结果一定比前一次的更优。当连续7次迭代都不能找到可行解时，程序就会自动判定优化过程已发散并自动结束寻优运算。零阶法采用拟合近似法寻优，由于寻优过程不需求当前点处的梯度，因此它可以较快的速度在最优点附近找到可行解。虽然零阶法无法像一阶法那样具有很高的求解精度（当然精度越高，耗时越多），但它的求解速度相当可观［4-5］。

另外，由于零阶法是一种全局搜索的算法，因此它不会像一阶法那样在局部极值附近过早收敛，得出并非我们期望的结果。所以，对于任何一个负责的工程优化项目都应先用零阶法找出最优解的大致位置，然后再用一阶法将其锁定。这样才能保证得到的最优解是真正的全局最优解，而不是局部极值点［6］。

由图4可知，迭代产生的某些点是可行解，但与最优点相去甚远；还有一些点在重量上虽优于第9次迭代结果，但它们都不是可行解。因此通过零阶法的近似搜索，可将第9次迭代结果暂做为最优点。

通过零阶法锁定最优解出现的大致位置，之后通过一阶法进一步寻优，以找出更加精确的最优解。一阶法迭代结果如图6和图7所示。

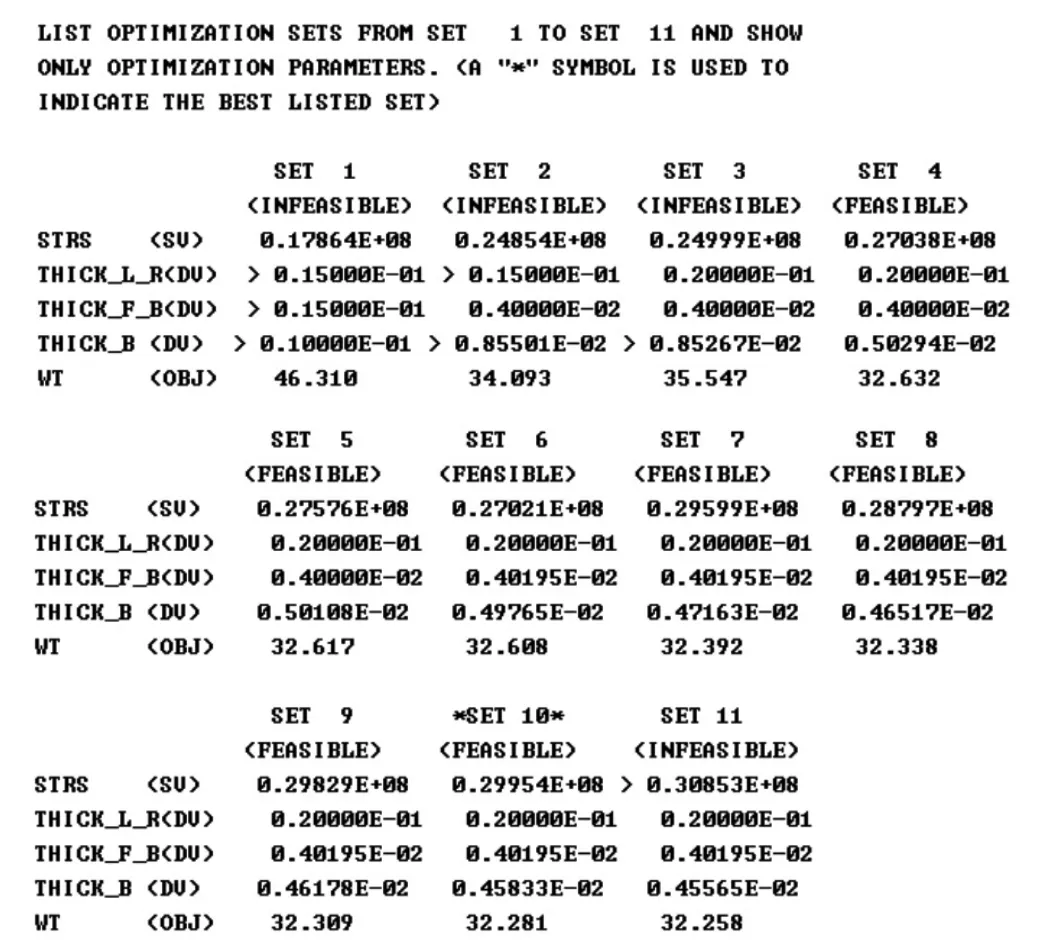
图6　一阶法迭代结果

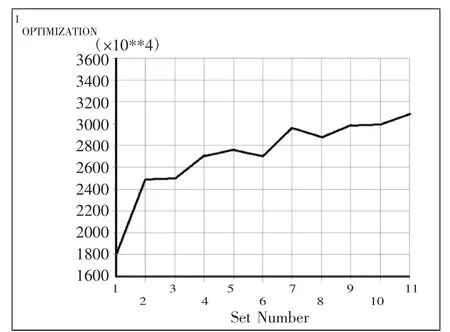
图7　一阶法目标函数迭代结果

从图5和图7可以看出，一阶法与零阶法得出的最优解相差并不大，但一阶法得出了更加精确的结果。通过零阶和一阶法两种结果的综合，可以确定第10次迭代的结果为最优解。最后将结果圆整为：箱体前后板厚THICK_F_B=5 mm；左右板厚THICK_L_R =5 mm；底板的厚度THICK_B=20 mm.

4　结束语

通过有限元优化设计方法对课题组研发的小型甘蔗收获机第二代样机的模块进行优化设计，实现甘蔗收获机的轻量化设计，以达到节约成本的目的。

［1］郭历伦，陈忠富.扩展有限元方法及应用综述［J］.力学季刊，2011，（3204）：612-625.

［2］陈锡栋，杨婕.有限元法的发展现状及应用［J］.中国制造业信息化，2010，39（28811）：6-8，12.

［3］曾志华，虞伟建.ANSYS结构优化技术在机械设计中的应用［J］.中国制造业信息化，2009，38（26613）：33-37.

［4］朱容庆.重型载重汽车车架轻量化设计研究［D］.武汉：武汉理工大学，2006.

［5］王玉艳，孙丽萍，王晓伟.基于ANSYS的客车车体轻量化技术及其应用［J］.大连交通大学学报，2007，（11002）：25-29.

［6］赵韩，钱德猛.基于ANSYS的汽车结构轻量化设计［J］.农业机械学报，2005，（06）：12-15.

Technology Overview of Finite Element Analysis and Optimization

CHEN Xi1，ZHANG Biao2，
（1.College of Mechatronics Engineering，Beijing Institute of Technology，Beijing 100081，China；2.College of Mechanical Engineering，Guangxi University，Nanning 530004，China）

This paper introduces the application of finite element analysis in engineering and optimization design methods using the finite element optimization software ANSYS.Aimed at the problem of lightweight design of small sugarcane harvester cutter gearbox，respectively using the methods of zero-order and first-order，optimization calculation of enclosure structure of gearbox is carried out，and the optimal solution is calculated，namely the front and rear thickness is 5mm，the left and right thickness is 5mm，the thickness of bottom plate is 20mm.This paper can provide a reference for lightweight design of small sugarcane harvester.

finite element；ANSYS；sugarcane harvester；gearbox

TH16：S225.5.3

A

1672-545X（2016）07-0013-03

2016-04-17

国家自然科学基金资助项目（51465006）；广西制造系统与先进制造技术重点实验室开放课题（11-031-12S04）；广西高校临海机械装备设计制造及控制重点实验室课题（GXLH2014KF-04）。

陈曦（1991-），女，河北唐山人，硕士研究生，研究方向：智能探测与控制；张彪（1991-），男，河北唐山人，硕士研究生，研究方向：先进制造技术及CAD/CAM。