一次函数图象上的关键点

□侯怀有　苗　伟

一次函数图象上的关键点

□侯怀有苗伟

一次函数图象与坐标轴的交点，两个一次函数图象之间的交点，常常是求解一次函数问题的关键点.理解这些点的坐标的几何意义，用好这些点的坐标，常常成为解决一次函数问题的关键.

【一】一次函数图象与x轴的交点

由一次函数与一元一次方程（不等式）的关系，函数图象与x轴交点的横坐标即为对应方程的解；反之，方程的解即为函数图象与x轴交点的横坐标.以图象与x轴交点（即方程的解）为分界，函数图象在x轴的上方和下方的部分分别表示y＞0或y＜0.

例1已知一次函数y=ax+b的图象经过点（6，0）和点（-2，4），求不等式ax+b＞0的解集.

分析：要求不等式ax+b＞0的解集，即是求一次函数的图象在x轴上方的x的取值范围.

解：以点（6，0）和点（-2，4）画直接y=ax+b的图象如图1，

由图可知，当x＜6时，函数y=ax+b的图象在x轴的上方，所以不等式ax+b＞0的解集是x＜6.

图1

【二】一次函数图象与y轴的交点

一次函数y=kx+b的图象与y轴的交点位置决定b的正负.与y轴正半轴相交，b＞0；与y轴负半轴相交，b＜0.

例2已知一次函数y=kx+b+6与一次函数y=-kx+b+2的图象的交点为（2，0），求这两个一次函数解析式及两直线与y轴围成的三角形的面积.

分析：将点（2，0）代入两直线的解析式中即可求出两个一次函数解析式，然后分别求出直线与y轴的交点坐标，进而求出三角形的面积.

图2

两条直线与y轴的交点坐标分别为（0，-2）、（0，2）（如图2），从而围成的三角形面积为

【三】两个函数图象的交点

两个函数图象的交点，一方面可利用坐标的几何意义求面积，另一方面还是两个函数函数值大小的分界点.

例3如图3，函数y=2x和y=ax+5的图象相交于A（m，3），则不等式2x＜ax+5的解集为.

分析：要求不等式2x＜ax+5的解集，只需确定点A的坐标即可.

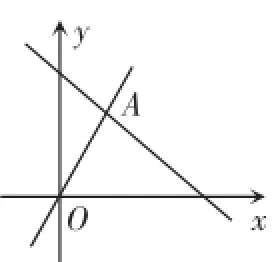
图3

解：因为点A（m，3）在函数y=2x的图象上，所以3= 2m，解得，所以点A的坐标为.由函数图象可知，当时，函数y=2x的图象在函数y=ax+5图象的下方，所以不等式2x＜ax+5的解集为