基于罗尔定理的两个积分中值问题

许宏文

(牡丹江师范学院数学科学学院, 黑龙江牡丹江157012)



基于罗尔定理的两个积分中值问题

许宏文

(牡丹江师范学院数学科学学院, 黑龙江牡丹江157012)

以变上限积分函数为纽带,建立了微分中值问题与积分中值问题的联系,构造相应辅助多项式,应用罗尔定理,证明两个带有二阶导数的积分中值问题.

罗尔定理； 辅助多项式； 变上限积分函数； 积分中值问题

1　引　　言

积分不等式的建立与积分估计是一元函数积分学部分的重要问题之一，在分析学中有着重要意义，这是因为在函数空间框架下的一些范数估计都与各种积分不等式的建立、积分估计相关.而建立相应的积分中值问题恰好是积分估计的有效方法，多年来积分中值问题在研究生入学考试试题中一直备受关注，2010年南京大学研究生入学考试数学分析第九题涉及如下的积分中值问题，记为定理1

定理1设函数f(x)在[a,b]上具有二阶导数, 则存在ξ∈(a,b)使得下式成立

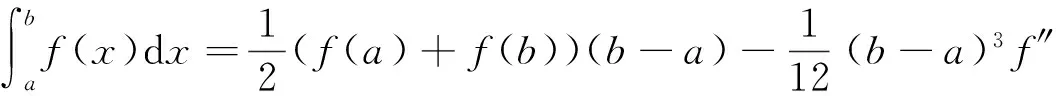
(1)

特别地，若f(a)=f(b)=0，则存在ξ∈(a,b)使得

(2)

在文献[1]中第242页有如下带有二阶导数的积分中值问题，本文记为定理2

(3)

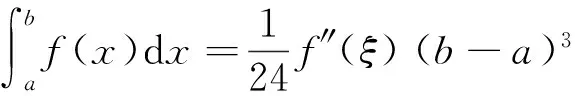
(4)

事实上借用变上限积分函数及其性质(见文献[2]296页)，上述两个带有二阶导数的积分中值问题分别与下面两个带有三阶导数的微分中值问题相对应，分别记为命题1和命题2.

命题1设函数f(x)在[a,b]上具有三阶导数，则存在ξ∈(a,b)使得

当f′(a)=f′(b)=0时，结论变为

命题2设函数f(x)在[a,b]上具有三阶导数，则存在ξ∈(a,b)使得

另外，2011年吉林大学研究生入学考试数学分析第四题涉及用定理3刻画的积分中值问题，如下

定理3设函数f(x)在[a,b]上可导, 则存在ξ∈(a,b)使得下式成立

特别地，若f(a)=0，则存在ξ∈(a,b)使得

与定理3对应的恰好是泰勒定理([2]定理5.3.2)，本文不再列出.

除前文列出的这样相互对应的三组积分中值问题与微分中值问题外，还有很多带有更高阶导数的积分中值问题与微分中值问题相互对应，这里不再一一列举.变上限积分函数作为连接微分学与积分学的纽带和桥梁，搭建了微分与积分的关系.微分中值定理作为处理微分中值问题的有效工具，同时也成为了处理积分中值问题和积分估计的有效手段，可见文献[3]和文献[4].本文应用文献[5]中证明微分中值问题的辅助多项式法，应用罗尔定理分别给出定理1和定理2的巧妙的证明.

2　两个带有二阶导数的积分中值问题的证明

综观文献[5]中证明微分中值问题的辅助多项式法可知，想构造恰当的辅助多项式应用罗尔定理来证明微分中值问题，可实现的前提是知道欲研究的函数在某些特定点的函数值或导数在某些点的值.但对定理1和定理2的一般情形，欲研究函数的信息过少，所以构造辅助多项式是困难的.本文，我们首先来证明定理1与定理2的特殊情形，即(2)式与(4)式成立，然后通过适当的辅助函数来证明其一般情形(1)式与(3)式成立.

证令

此时欲证明的积分中值问题转化成了微分中值问题

由变上限积分函数的性质可知，F三次可导，且有

F(a)=F′(a)=F′(b)=0.

想构造一个新的函数G(x)=F(x)-P(x)，其中P(x)为三次多项式，使得G(x)满足

G(a)=G(b)=G′(a)=G′(b)=0,

(5)

则P(x)满足P(a)=P′(a)=P′(b)=0，P(b)=F(b). 因P(a)=P′(a)=0，可令

P(x)=(x-a)2(Ax+B).

由P(b)=F(b)和P′(b)=0有

(b-a)2(Ab+B)=F(b),2(Ab+B)+A(b-a)=0,

解得

至此找到了需要的辅助多项式

辅助函数G(x)=F(x)-P(x)满足(5)式，在区间[a,b]上对函数G(x)应用罗尔定理,存在η∈(a,b)使得G′(η)=0，注意到G′(a)=G′(b)=0，对函数G′(x)在区间[a,η]和[η,b]上继续使用罗尔定理有，存在ξ1∈(a,η)和ξ2∈(η,b)使

G″(ξ1)=G″(ξ2),

对函数G″(x)在区间[ξ1,ξ2]上使用罗尔定理有，存在ξ∈(ξ1,ξ2)使得

(6)

即

注意到(6)式，所构造的辅助多项式的三次导数与问题相关，而辅助多项式中的二次项、一次项和常数项对问题的解决是没有影响的，待定常数B只与这些无关项相关，所以在计算过程中，只需计算出A的值，而无须计算B.

下面证明定理1的一般情形，即(1)式成立.

定理1(1)设函数f(x)在[a,b]上具有二阶导数, 则存在ξ∈(a,b)使得

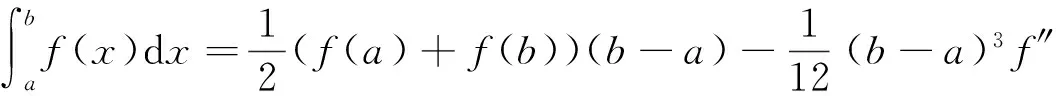
证令

显然，g(x)在[a,b]上满足g″(x)=f″(x)，g(a)=g(b)=0. 应用证毕的结论有

(7)

而

(8)

联立(7)与(8)有

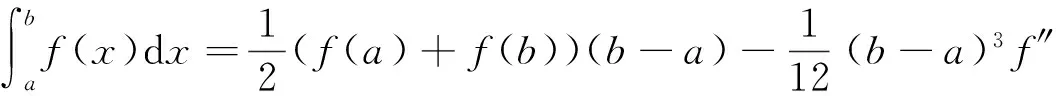
下面证明定理2.依然先来证明其特殊情形(4)式.

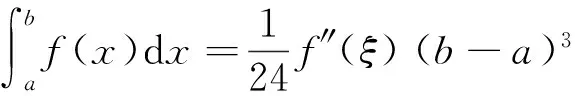
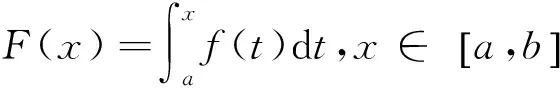
且有

我们想构造一个新的函数G(x)=F(x)-P(x)，其中P(x)为三次多项式, 使得G(x)满足

(9)

则P(x)满足

(10)

由(10)式可令

解得

G′(η1)=G′(η2)=0，

G″(ξ1)=G″(ξ2).

对函数G″(x)在区间[ξ1,ξ2]上使用罗尔定理有，存在ξ∈(ξ1,ξ2)使得

即

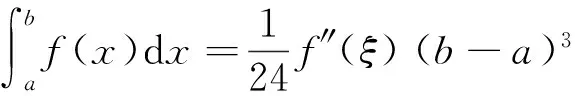
下面运用定理2的特殊情形(4)式，来证明定理2的一般情形(3)式成立.

应用(4)有

所以

对于本文给出的带有一阶导数的积分中值问题，即定理3，读者可用同样的方法给出证明，证明过程中，只需构造一个二次多项式即可.

3　总　　结

定理1和定理2的证明思路是引入变上限积分函数，把带有二阶导数的积分中值问题转化为带有三阶导数的微分中值问题，辅助函数选择辅助多项式与变上限积分函数的差，反复应用罗尔定理使问题得证.值得注意的是，就定理1与定理2的一般形式来讲，直接构造由变上限积分函数与辅助多项式和的形式的辅助函数，应用罗尔定理来证明是无法实现的.本文的巧妙之处在于考虑定理1和定理2的特殊情形，引入变上限积分函数，此时变上限积分函数的信息足够多，通过这些信息实现需要的辅助多项式的构造.对于两个更一般的积分中值问题，即定理1与定理2的一般情形，作为特殊情形的推论，再构造新的辅助函数，应用特殊情形的结论加以证明.

[1]裴礼文.数学分析中的典型问题与方法[M].北京:高等教育出版社, 2006：242-243.

[2]陈纪修, 於崇华, 金露.数学分析(上)[M].北京:高等教育出版社, 2004：168-296.

[3]赵显曾.两个积分不等式[J].大学数学, 2015,31(1): 78-80.

[4]郑权.基于微分中值定理证明微积分基本公式和积分中值定理[J].大学数学, 2003,19(6): 78-80.

[5]陈飞翔,冯玉明,刘金奎.证明微分中值问题的辅助多项式法[J].高等数学研究, 2010,13(5): 30-31.

Two Integral Mean Value Problems Based on Rolle Theorem

XU Hong-wen

(Institute of Mathematics, Mudangjiang Normal University, Mudanjiang Heilongjiang 157012, China)

We establish the relation between the differential and integral mean value problems by using the integration with varying upper bound. Then we construct the corresponding auxiliary polynomial and ap-ply Rolle theorem to solve two mean value problems with second-order derivatives.

Rolle theorem; auxiliry polynomial; integration with varying upper bound; integral mean value problem

2015-06-19；[修改日期]2016-05-13

2013年黑龙江省高等教育教学改革项目(省文序号497)

许宏文(1974-),女, 博士, 副教授, 从事微分包含定性理论研究. Email:xhwmdj@163.com

O175.2

C

1672-1454(2016)04-0073-05