组元厚度结构对层状声子晶体导带的影响

唐启祥，邱学云，胡家光

（文山学院信息科学学院，云南文山　663099）

组元厚度结构对层状声子晶体导带的影响

唐启祥，邱学云，胡家光

（文山学院信息科学学院，云南文山663099）

以三组元层状声子晶体为例，采用一定的中心频率确定各组元的中心波长，以各组元中心波长的倍数为该组元的厚度系数，以不同组元与某一组元的厚度系数之比为相应的厚度系数比，采用传输矩阵法计算传输特性，研究了不同厚度系数、厚度系数比及原胞数对声子晶体的传输特性的影响。结果显示，导带分布具有非常完美的对称性，且每个导带的频率中心值、导带宽度以及相邻导带频率中心的间隔均随厚度系数及厚度系数比的变化呈现明显的变化规律，而与原胞数无关。

声子晶体；导带；中心波长；厚度系数；厚度系数比

［DOI］10. 3969 / j. issn. 2096-2266. 2016. 06. 006

声子晶体是密度和弹性常数呈周期性变化的人造带隙材料。根据材料的形状和排列方式不同，可分为一维、二维和三维声子晶体。根据组元的不同，每一维的声子晶体又可以分成二组元、三组元甚至更多组元的结构材料。已有丰富的研究结果表明，不同的密度和弹性常数，对声子晶体的带隙均具有相应的影响〔1-9〕。刘启能对二组元的情况作了解析研究〔10〕，对三组元的斜入射情况作了模拟计算研究〔11〕。文献中注重对二组元层状或杆状的带隙的变化进行研究，而本文作者在对三组元层状结构的声子晶体进行研究时发现，合理选择各组元材料的厚度，禁带的变化特征不显著，但导带的分布及其变化则表现出非常强的规律性。

1　模型和理论

设3种不同密度和弹性常数的组元A、B和C均为无限大平面材料，并沿z轴方向依次排列，置于外界均匀弹性介质E（未单独画出）中，平面弹性横波和纵波自E垂直于材料A沿z轴方向传播，如图1所示。

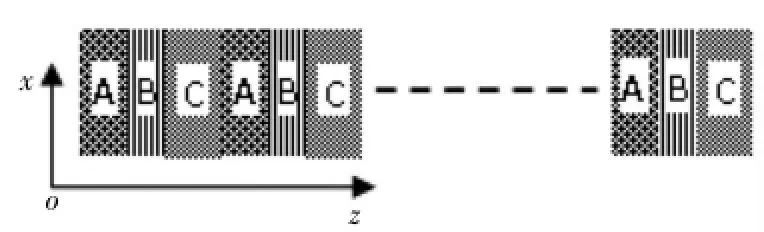
图1　一维三组元声子晶体的结构模型

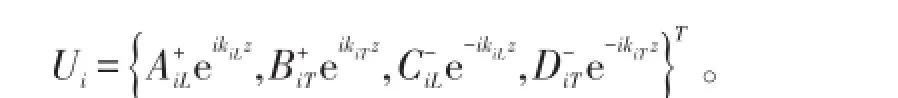
当位移波矢Ui通过一个界面后变成新的位移波矢Uj，Ui与Uj之间的转换关系为：

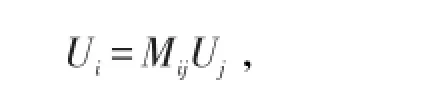
式中Mij为从介质i到相邻介质j（j为A、B或C）的转移矩阵，根据胡克定律及弹性波的位移和应力在界面两侧的z分量和x分量的连续条件可得到。

其中

弹性波通过厚度为di的介质i，波矢的相位发生变化，相应的传递矩阵为

弹性波通过置于均匀弹性介质E中具有N个原胞的整个声子晶体的传递矩阵为

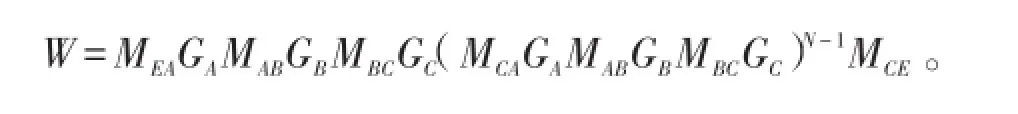
由W的矩阵元求得纵波透射率TL和横波的透射率TT分别为

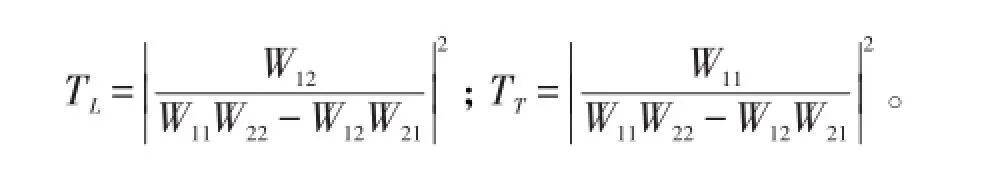
2　实例计算

以钢、环氧树脂和塑料构成晶体材料，置于有机玻璃中。有关材料参数如表1所示。

表1 材料参数

具有N个原胞的声子晶体的厚度：

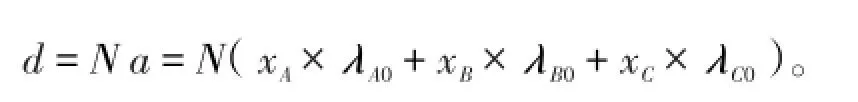
为便于讨论，设定xA=xB=xC=x。则有

图2　纵波透射率谱图

2.1厚度系数对导带频率中心及间隔的影响固定原胞数N=4，改变厚度系数x（实际上在改变晶格常数d），分别为0.1，0.2，…，1.0，选择第二导带计算它的频率中心 f20和相邻导带频率中心的间隔Δf0，结果显示，导带的频率中心 f20和相邻导带频率中心间隔Δf0均随厚度系数增大而减小，如图3和图4所示。

图3　第二导带频率中心随厚度系数变化的响应曲线

图4　相邻导带频率中心间隔随厚度系数变化的响应曲线

2.2厚度系数对导带宽度的影响在图2中，存在两种宽度的导带，现在分别计算它们的宽度与材料厚度系数之间的变化关系。见图5。

图5　厚度系数对导带宽度的影响曲线

结果显示，无论是宽带还是窄带的宽度Δf均随厚度系数x增加而减小。

（1）在e＜1的范围内，导带频率中心间隔保持2.5 kHz不变，但是随着e的增大，宽带位置向低频方向运动，相邻宽带之间的窄带数量随之减少；

（2）当e=1时，各导带之间的间隔变成完全一样，但窄带变成不完整的缺陷状；

（3）随着e＞1，导带频率中心间隔与e成反比例减小，相邻2个导带之间的窄带数量逐渐增多，透射率谱线逐渐变得密集。如图6所示。

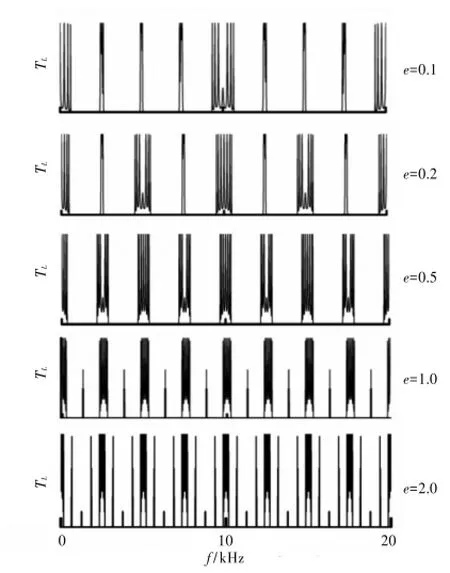
图6　厚度系数比对导带分布影响的对比图

2.4原胞数对导带的影响保持其他参数不变，改变原胞数N，计算导带的频率中心值和相邻导带的频率间隔。结果发现：

（1）N不影响导带的频率中心值；

（2）导带间隔随原胞数N量的增加而减小，导带宽度变宽，导带内的透射率谱线变得致密。

由于篇幅原因，在此不再给出其他图像。

3　结果的理论分析

声子晶体的导带或带隙均是不同频率弹性波在相邻组元界面上来回反射叠加出现的结果。当各组元的厚度刚好为波长的整数倍或分数倍时，由该组元引起的相位延迟将会是π的整数倍数或分数倍。根据Bragg散射机理，整数倍中偶数倍的被透射，奇数倍的被反射。在不考虑吸收的情况下，一定频率的波通过某组元，一般同时伴有反射和透射。当不同频率的波通过多层这样的组元材料后，在某些频段刚好被完全反射，形成带隙，而刚好能通过的频段即成为导带，且导带宽度不一定会和带隙宽度一样。当波的频率变化范围足够宽后，这种带隙和导带相间分布的现象又会重复出现，于是便出现了本研究中得到的结果。

4　结论

将各组元的厚度与其中心波长的比值取名为厚度系数x，通过改变厚度系数来改变各组元的厚度，改变厚度系数的比值来改变组元的厚度比e，计算了一维三组元声子晶体导带随厚度系数x和厚度比e变化的一些规律。结果发现：

（1）随厚度系数x增大，每个导带的频率中心和相邻导带频率中心间隔、宽带和窄带的频率宽度均逐渐减小。

（2）厚度系数比在不同范围内，对导带产生的影响不一样。在e＜1的范围内，导带频率中心间隔保持不变，但是随着e的增大，宽带位置向低频方向运动，相邻宽带之间的窄带数量随之减少；当e=1时，各导带之间的间隔变成完全一样，但窄带变成不完整的缺陷状；随着e＞1，导带频率中心间隔逐渐减小，相邻2个导带之间的窄带数量逐渐增多，透射率谱线逐渐变得密集。

（3）随原胞数N的增加，各导带的频率中心值不变，但是导带宽度变宽，导带内的透射谱线变得致密。

以上结果可以用来指导弹性波波导的设计和制造。

〔1〕杨旭，王立勇，杜晓东，等.一维三组元准周期结构声子晶体的透射性质〔J〕.内蒙古师范大学学报（自然科学汉文版），2010，39（4）：363-366.

〔2〕曹永军，董纯红，周培勤.一维准周期结构声子晶体透射性质的研究〔J〕.物理学报，2006，55（12）：6470-6474.

〔3〕曹永军，胡晓颖，周培勤.一维准周期结构声子晶体带隙特性的研究〔J〕.内蒙古师范大学学报（自然科学汉文版），2008，37（1）：53-57.

〔4〕刘超.一维声子晶体杆状结构纵向振动带隙特性〔J〕.激光杂志，2013，34（5）：47-48.

〔5〕刘启能.一维声子晶体中弹性波的全反射贯穿效应〔J〕.振动与冲击，2012，31（1）：173-176.

〔6〕曹永军，杨旭，姜自磊.弹性波通过一维复合材料系统的透射性质〔J〕.物理学报，2009，57（11）：7735-7738．

〔7〕邱学云，胡家光.一维三组元杆状结构声子晶体带隙研究〔J〕.重庆师范大学学报（自然科学版），2013，30（2）：102-107.

〔8〕刘启能.一维声子晶体的传输特性〔J〕.人工晶体学报，2008，37（1）：179-182.

〔9〕宋玉敏，高云，王雪文，等.一维声子晶体的振动特性研究〔J〕.云南师范大学学报（自然科学版），2010，30（2）：44-48.

〔10〕刘启能.一维声子晶体中声波能带的解析研究〔J〕.应用力学学报，2011，28（2）：185-188.

〔11〕刘启能.弹性波斜入射声子晶体的传输特性〔J〕.应用力学学报，2009，26（2）：397-401.

〔Abstract〕Choosing a central frequency to calculate the central wavelength of every component，and determining every component's thickness coefficients with ratios of their central wavelength，and defining each component's ratio of thickness coefficient with a certain component's thickness coefficient，and the transmission characteristics of the three components phononic crystal were calculated with transfer matrix method for different thickness coefficient and ratio of thickness coefficient.The results show that the distribution of the conduction band presents very perfect symmetry.With the changing of the thickness coefficient and the thickness coefficient ratio，all of the frequency center of the conduction band and the conduction band width and the center of the adjacent conduction band frequency interval present obvious regularity，but there is nothing to do with the changing of the original cell number.

〔Key words〕phononic crystal；conduct band；central wavelength；thickness coefficient；ratio of thickness coefficient

（责任编辑袁霞）

Effect of Component Thickness Structure on Layered Phononic Crystal Conduct Band

Tang Qixiang，Qiu Xueyun，Hu Jiaguang
（College of Information Science，Wenshan University，Wenshan，Yunnan 663099，China）

TH113

A

2096-2266（2016）06-0023-04

云南省教育厅科学研究基金资助项目（2014Y474）

2016-03-28

2016-04-08

唐启祥，副教授，主要从事材料物理研究.