基于指数化主成分分析的国民生产总值应用研究

时志刚

江西财经大学信息管理学院，江西　南昌　330013



基于指数化主成分分析的国民生产总值应用研究

时志刚*

江西财经大学信息管理学院，江西南昌330013

在对原始数据进行主成分分析之前，采用指数化的方法对原始数据进行预处理。利用指数化主成分分析方法对全国各省市影响GDP增长的因素进行分析，使用Matlab软件对数据进行仿真模拟，以princomp函数输出结果为根据，提取出反映GDP增长的主成分，为经济决策提供理论支持。

GDP；指数化；主成分分析；指标体系；Matlab

一、引言

一般情况下，在对某一事物进行实证研究时，为了更加全面、准确的反映事物的内在特征或发展规律，经常要考虑与此事物有关的多个指标。这样就产生了如下问题：一是为了避免遗漏重要的信息而分析尽可能多的指标，二是指标增多就增加了问题的复杂性，而且因为这些指标都是对同一事物的反映，容易造成信息重叠、冗余。为了解决这一问题，人们提出了主成分分析的多元统计方法，使得在定量研究中涉及的变量尽可能的少，而反映的信息尽可能的多[1]。

主成分分析(PCA)又称为主分量分析，是一种利用降维思想，在损失少量信息的情况下，通过线性变换，把反映事物内在特征的多个指标转化为几个综合指标的多元统计方法。通常把转换之后的几个综合指标称为主成分，各个主成分都是原始变量的线性组合且相互之间线性独立，由此以来，在研究较为复杂的问题时就可以通过考虑少数几个主要成分来反映数据信息的内在特征，使得要研究的问题得到简化，从而提升分析效率，而且不至于造成太多的信息丢失。

求解主成分的过程就是对数据矩阵结构进行分析的过程，在实际的操作中，我们可以从原始数据的协方差矩阵出发求解主成分，也可以从原始数据的相关矩阵出发求解主成分，总之，数据矩阵容易受到数量级和量纲影响，一般情况下，在分析之前，要对原始数据进行预处理，尽可能的减少或消除数量级和量纲的影响[2]。传统的由SPSS软件对数据进行的标准化处理，数据协方差矩阵转化为相关系数矩阵，这样使得各指标的方差变为1，去除了各指标变异程度的差异，但却不能够完全反映原始数据包含的全部的信息，造成信息丢失[3-4]。鉴于此，本文利用指数化方法改进传统的主成分分析方法。

二、指数化主成分分析方法

在对原始数据进行主成分分析之前，将数据进行标准化处理，在此采用指数化的方法对原始数据进行标准化处理，提高分析结果的准确性。

指数化处理以指标的最大值和最小值的差距进行数学运算，其结果介于0-1之间。若存在由m个样本组成的样本集x，每个样本有n各指标，则第i个样本的第j个指标值为xij(i=1，2，…，m；j=1，2，…，n)。对xij进行标准化的具体计算如下：

zij=(xij-xmin)/(xmax-xmin)

其中，zij为标准分数，xij为某样本在某指标下的指标值，xmax为某指标下全部样本的指标之中的最大值，xmin为某指标下全部样本的指标之中的最小值。经过这样的标准化处理之后，原始数据转化为无量纲化指标值，使得所有的指标值都处在同一个数量级别上。

指数化数据处理方法既满足了对数据进行标准化预处理的要求，又消除了指标量纲上的差异，比较准确的反映了数据的原始信息，克服了标准化处理方法的不足，为之后的主成分分析研究提供了基础。

三、利用指数化主成分分析方法研究国民生产总值增长情况

改革开放以后，我国经济和社会发展取得巨大成就，2010年读中国国内生产总值(GDP)比日本超越日本高出4000多亿美元，超越日本成为全球第二大经济体。新时期下，我国经济发展面临一系列挑战，如何妥善应对，适应经济发展新常态，不断创新宏观调控方式，推动形成经济结构优化、发展动力转换、发展方式转变加快的良好态势，是我们要着力解决的问题，而衡量经济发展状况的重要指标即是GDP。

GDP是国民经济核算的核心指标，也是衡量一个国家或地区总计经济状况的重要指标，而影响GDP增长的因素，总的来说，包括三大产业的增加值，详细划分主要体现在：农林牧渔业增加值、工业增加值、建筑业增加值、批发和零售业增加值、交通运输、仓储和邮政业增加值、住宿和餐饮业增加值、金融业增加值、房地产业增加值等方面。

由于我国幅员辽阔，物质基础、资源能源分布不均，环境状况不同，使得我国经济发展不平衡状况明显。因此，对我国各地区GDP增长的各项指标进行统计分析，综合出全面的反映我国各地区GDP增长情况的主要因素，为我国实施结构性改革，推动新旧动能接续转换和经济结构的转型升级，促进我国经济又好又快发展，提供合理的决策依据。

表1　我国各地区GDP增长指标体系

(一)构建GDP增长指标体系

要分析研究我国经济发展情况，必须构建一套科学完整的指标体系，全面、客观、真实的评价我国GDP增长状况，要严格遵循整体性、针对性、系统性、科学性和可操作性原则。根据指标体系构建原则和影响GDP增长的因素构成，本文构建了我国各地区GDP增长指标体系如表1所示。该指标体系包含8项反映我国GDP增长状况的指标，根据该指标体系，以2014年我国各地区GDP增长状况数据(来源于国家统计局——中国统计年鉴)为研究样本，分析研究我国GDP增长构成情况。

图1　各省市两个主成分得分值散点图

地区GDP总增加值第一主成分得分值西藏638.840青海1947.540.0446宁夏2301.580.0802海南2974.020.1708甘肃5433.370.2551新疆7614.20.3567贵州7657.350.4162吉林11645.780.48山西10707.070.4986天津12842.460.5099云南10401.930.5481重庆11905.440.6074江西13423.530.619黑龙江12284.320.6333广西13482.180.6655陕西15257.930.6781内蒙古15580.010.7682北京13220.660.783安徽18062.070.7888上海18305.760.9097福建20820.040.9798湖南21400.21.0007湖北22569.261.0927辽宁24274.911.1167四川23970.471.1755河北26129.521.2188河南30150.531.4555浙江33304.531.5722山东50368.932.314江苏53230.362.4949广东55515.492.5416

表3　两方面GDP增加值之差和第二主成分得分值

(二)利用指数化主成分分析方法对各省市GDP增长情况进行matlab仿真模拟分析

随着动力系统和非线性科学的迅猛发展，对数学人才在微分方程知识方面的要求逐步提高，教师应该与时俱进，针对常微分方程课程的特点，用科学发展的眼光不断革新教学内容与方法。只有这样，才能提高学生学习常微分方程的积极性和主动性，培养学生的创新意识，提高学生应用知识解决实际问题能力，最终实现“学数学”、“用数学”的教育目标。

1.指数化后的数据主成分分析

使用Matlab软件，针对指数化后的全国各省市的GDP增长状况样本数据，利用princomp函数进行主成分分析，输出矩阵所对应的协方差矩阵的所有特征向量组成的矩阵COEFF、各主成分的得分数据SCORE以及协方差矩阵的特征值LATENT。利用数据的Matlab运行结果输出，作进一步的分析研究。

根据样本相关系数矩阵的特征值LATENT，通过计算特征值和所有特征值总和的比值得出各个主成分的贡献率Explained。

Explained=[83.459，10.323，1.997，1.643，1.192，0.698，0.555，0.133]

由此可以看出，前两个主成分的贡献率已经达到了93.782%，后面6个主成分的贡献率相对较小。因此，在这里只选取前两个主成分作为代表，作进一步的分析。

结合主成分表达式的系数矩阵COEFF，可以得出前两各主成分的系数表达式：

y1=0.29x1+0.38x2+0.35x3+0.37x4+0.36x5+0.37x6+0.33x7+0.37x8

y2=0.69x1+0.05x2+0.27x3-0.24x4+0.05x5+0.11x6-0.53x7-0.31x8

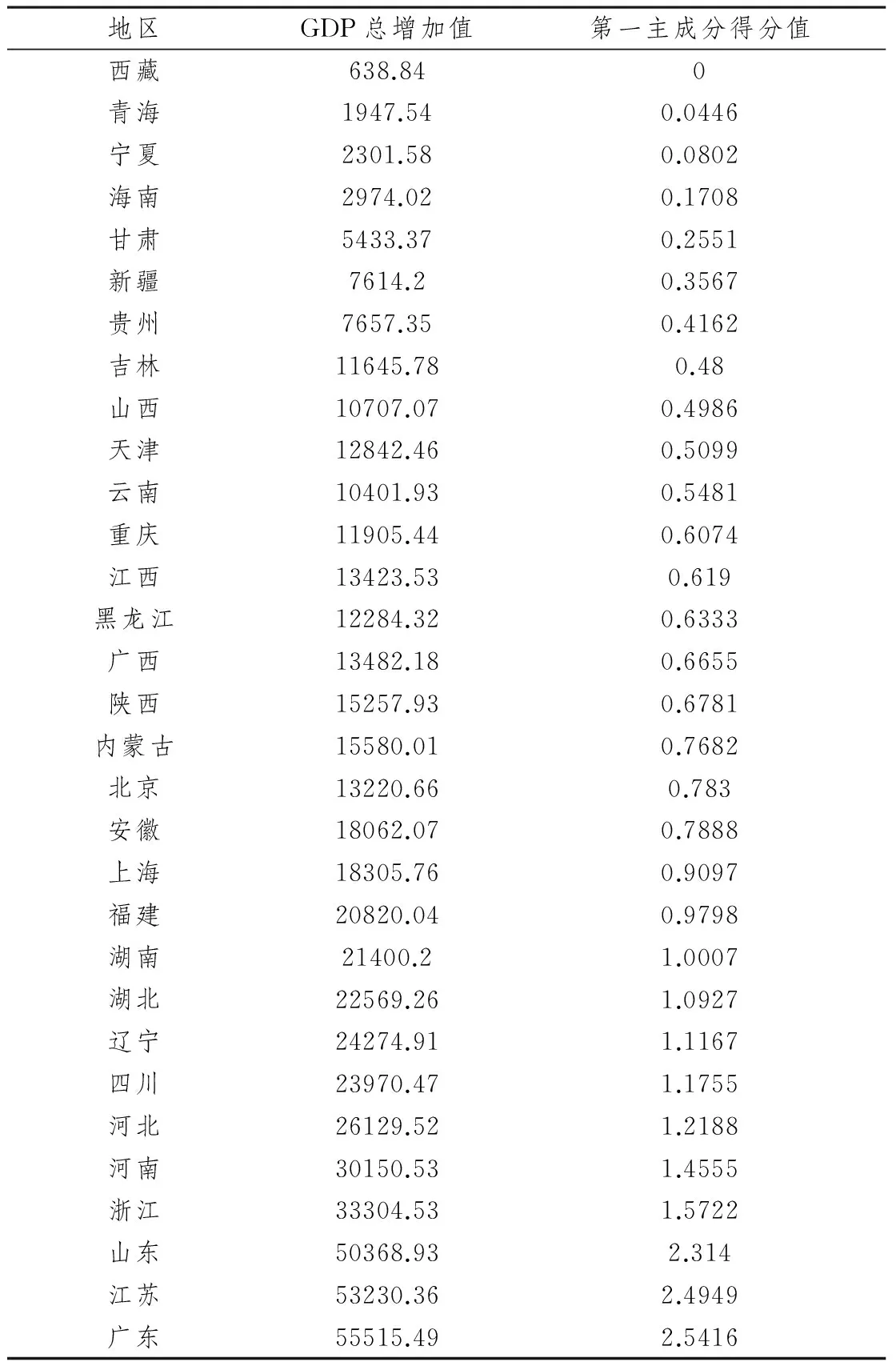
从第一主成分的表达式中可以看出，每一个指标变量都有接近的正载荷，说明每个指标对第一主成分的影响是相近的。这样以来，可以将指数化之后的全国各地区的各个GDP的增加值指标数据汇总并计算出各地区GDP的总的增加值，并按照第一主成分得分的大小由高到低进行排列，结果如表2所示。

从表2中可以看出，每一个地区的GDP的总增加值与第一主成分得分数据基本呈正比例。因此，第一主成分反映了全国各地区GDP增加值的整体水平，可以用第一主成分作为整体的GDP增加值影响成分。

3.第二主成分分析

从第二主成分的表达式中可以看出，评价指标农林牧渔增加值、建筑业增加值呈正载荷，金融业增加值、房地产业增加值呈负载荷，由此可以反映出农林牧渔业和建筑业的增加值、金融业和房地产业的增加值对整个地区GDP增加值的影响两个方面的对比。计算出这两个方面GDP增加值之差，并按照第二主成分的得分值由小到大排列，结果如表3所示。

从表3中可以看出，这两个方面的GDP增加值之差与第二主成分得分基本成正比关系，通过比较发现，从地区的经济地位和产业结构来看，上海、北京、广东、天津、浙江、江苏等在金融业和房地产业方面对GDP增加值的影响较大，而河南、湖南、四川、河北、山东、湖北、黑龙江等在农林牧渔业和建筑业方面对GDP增加值的影响较大。综合考虑其主要原因是上海、北京、广东等地区处于经济比较发达的地区，金融业和房地产业对相关地区GDP的贡献值较大，而河南、四川、黑龙江等地区的产业结构中第一产业占据相当大的份额，因此，其农林牧渔业和建筑业对相关地区GDP的贡献值较大。因此第二主成分可以当做结构性GDP增加值影响成分。

(三)综合分析

为了分析各省市在主成分所反映的经济意义方面的情况，对使用指数化方法进行标准化之后的原始数据代入主成分表达式计算出各省市的主成分得分，将各省市的主成分得分值在二维空间中描述出来，得到其分布情况的散点图，如图1所示。

从图1中可以看出，第一主成分得分较高的省市有广东、山东、江苏、浙江、河南，这些地区的总的GDP增加值较高；而总的GDP增加值较低的西藏、青海、宁夏、海南、甘肃、新疆，第一主成分的得分值也较低，这说明第一主成分反映了综合的GDP增加值水平的高低。

另外，经济较为发达的北京、上海、广东、天津、浙江等地，第二主成分得分较低，而河南、四川、湖南、黑龙江等地第二主成分得分值较高，这主要是由经济结构不同引起的，经济发达地区金融业、房地产业等对地区GDP增长的影响较大，经济欠发达的地区农林牧渔业、建筑业等对地区GDP增长的影响较大。

四、结束语

利用指数化主成分分析方法对GDP增加值情况进行分析，能够降低使用传统的主成分分析的数据标准化方法产生的原始数据失真的影响，分析结果更加合理、准确，为进一步的研究建立了基础，各省市可以根据对影响GDP增加值的各指标主成分分析的结果，在提高传统优势产业的发展水平的基础上，科学合理的调整产业结构，转变经济增长发展方式，加强地区间的交流互动，优势互补，促进经济又好又快发展。

[1]何晓群.多元统计分析(第四版)[M].北京：中国人民大学出版社，2015.

[2]纪荣芳.主成分分析法中数据预处理方法的改进[J].山东科技大学学报，2007(12)：95-98.

[3]王亚雄，李建英.主成分分析方法在多元质量控制中的应用[J].工业工程与管理，2005，10(3)：121-125.

[4]李竹逸，徐琤.数据预处理在基于主成分分析质量管理中的作用[J].商业文化，2012(2)：175.

[5]李红松，邓旭东.统计数据分析方法与技术[M].北京：经济管理出版社，2014.

[6]赵喜林，李德宜，龚谊承.应用数理统计与spss操作[M].武汉：武汉大学出版社，2014.

时志刚，江西财经大学信息管理学院，管理科学与工程专业硕士，研究方向：管理决策。

F275；F832.51

A

1006-0049-(2016)19-0093-03