陀螺加速度计伺服回路的滑模变结构控制方法研究

颜晓虹，严小军，张沛晗，岳 辉，章丽蕾

（北京航天控制仪器研究所，北京100039）

陀螺加速度计伺服回路的滑模变结构控制方法研究

颜晓虹，严小军，张沛晗，岳 辉，章丽蕾

（北京航天控制仪器研究所，北京100039）

陀螺加速度计的正常工作需要相应的伺服回路来保证仪表具有足够的静态和动态性能，以陀螺加速度计伺服回路为研究对象，对其控制方法进行研究。基于已有的数字控制方案，针对陀螺加速度计伺服回路的参数摄动等不确定问题，设计了一种离散域内的滑模变结构控制器，并对其进行相关仿真和实验。仿真和实验结果表明，滑模变结构控制器的动态性能良好，具有较强的鲁棒性。

陀螺加速度计；伺服回路；离散；滑模变结构

0　引言

陀螺加速度计是战略导弹和运载火箭导航系统中的核心器件，其作用是敏感载体的加速度，从而得到载体导航所需要的加速度、速度和位置信息，其精度的高低对整个制导系统至关重要［1］。而陀螺加速度计的正常工作必须有相应的伺服回路来保证仪表具有足够的动静态性能和稳定性，所以，伺服回路的性能对整个仪表的精度起着重要作用，本文就是在数字控制系统的基础上，对伺服回路进行控制算法的设计，从而提高系统的精度和稳定性。

基于经典控制理论的设计方法来设计控制器是目前工程上常用的方法，该方法物理意义简单明确，计算和绘图也很方便，至今沿用不衰。但是，经典控制理论假设的前提是确定性系统，而对非理想陀螺加速度计系统而言，存在着诸如参数摄动、环境运行条件变化等不确定性因素，因此，本文选择了鲁棒性较强、适用于不确定性系统的滑模变结构控制器对其进行改进。

滑模变结构控制系统的基本原理在于，当系统状态穿越状态空间的滑动超平面时，反馈控制的结构就发生变化，从而使系统性能达到某个期望指标。由此可以看出，变结构控制系统能够通过控制器本身结构的变化，使得系统性能一直保持高于一般固定结构控制所能达到的性能，且到达滑模后动态品质不受系统本身的模型参数和外部干扰影响，具有很强的鲁棒性［2］。

1　陀螺加速度计的数学模型

根据陀螺加速度计的运动方程可得到陀螺加速度计系统方块图，如图1所示。

图1　陀螺加速度计系统方块图Fig.1 Block diagram of PIGA system

陀螺部分的传递函数为［3］:

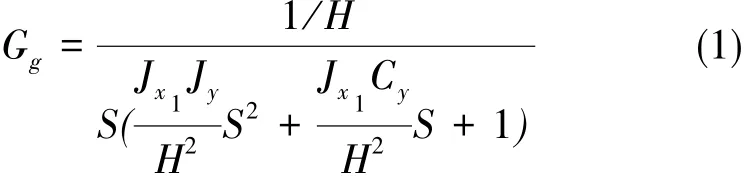
其中，aX1为仪表沿外框架轴的输入视加速度；ml为仪表绕内框架轴的摆性；H为仪表角动量；MX1为绕外框架轴的各种干扰力矩之和；MD为力矩电机的力矩；K0为电子部分的增益；G（S）为校正网络传递函数，并设G（0）=1；Jx1、Jy为分别为外框架组件绕x1轴和内框架轴组件绕y轴的转动惯量；Cy为绕内框架轴的阻尼系数。

现为了设计滑模变结构控制器，需将已建立的传递函数模型转化为状态空间表达式模型。本文是将传递函数转化为能控标准型的状态空间形式，且为了设计离散滑模变结构控制，需对其进行离散化处理。

首先将式（1）转换成能控标准型的状态空间方程:

其中，x1为内框架轴相对外框架的转角。

由于设计的是数字控制器，所以我们在离散域进行滑模变结构控制的设计。将式（2）表示的伺服回路模型经离散化处理（采样周期为2kHz）后得到式（3）表示的离散状态空间方程［4］。

2　滑模变结构控制器设计

滑模变结构控制的关键在于选取合适的滑模面切换函数s（x），从中求解不连续控制函数u+（x）或u-（x），使s（x）=0以外的运动点在有限时间内到达切换面，并保证s（x）=0滑模运动具有稳定性，以此获得良好的系统动态性能。

离散滑模与连续滑模控制有很大不同，由于采样频率的存在，滑模变结构控制不能产生理想的滑动模态，只能产生准滑模控制。所谓准滑动模态是指系统运动轨迹被限制在理想滑动模态的某一邻域内，此邻域称为滑动模态的 “边界层”。离散滑模变结构控制既要解决运动点边界层外的渐近稳定问题，又要解决运动点边界层内的抖动及原点收敛问题，本系统的离散滑模变结构控制主要是解决这两个问题［5］。

设切换面为:

其中，Ce=［c1c21］为待求矩阵，E为给定信号与输出信号之间的误差，为给定信号），只要合理地选择c1、c2，式（4）就可具有稳定的准滑动模态。

由式（4）可得:

将式（5）变形可得式（6）:

本文采用指数趋近律来改善动态品质。其特点是运动点趋近过程中的趋近速度是变化的，具有加快趋近速度和削弱抖动的优点。连续域内的指数趋近律表达式为:

其中，s为连续域内的切换面。相应地，离散域内的指数趋近律表示为:

即，s（k+1）=（1-qTs）s（k）-εTssign（s（k））（8）

其中，Ts为采样周期，只要满足qTs＜1，趋近律在带宽为εTs的s（x）=0区域内为渐近稳定，趋近模态具有良好品质。将式（8）代入式（6）中，可得控制律:

上述4个参数中的q主要影响切换函数的动态过程，适当调整该参数可以改变系统向滑模面的趋近速度，q越大，系统到达滑模面的速度越快。对于切换函数的设计，主要是设计参数c1和c2，保证滑模运动渐进稳定且具有较快的动态响应速度，它们越大，滑模运动段响应越快，快速性越好。因此，增大q、c1和c2都可以相应地提高系统的快速性，但是参数过大会导致控制量过大，且在实际控制中会引起抖振。ε是系统克服摄动及外干扰的主要参数，ε越大，系统克服摄动及外干扰的能力越强，但是如果过大将会导致系统抖振的加大。因此，我们必须合理地选择这4个参数［6］。

利用极点配置的方法可计算出c1和c2的值，而ε和q则可通过仿真试验得到，最终取值为c1= 115000，c2=1680，k=15，ε=40。

3　仿真验证

现通过Matlab软件对设计的离散滑模变结构控制器进行仿真，以验证其正确性。

我们将设计的滑模变结构控制器代入图1（a）所示的陀螺加速度计系统方框图（输入为加速度a，输出为 ˙α）中进行仿真验证，建立的Simulink模型，如图2所示［7］。

其中，采样时间设置为2kHz。仿真结果如图3所示，且将其与PID控制的系统阶跃响应进行比较。

由图3可知，采用滑模变结构控制时，系统的调节时间为45ms，超调量约为9.8%，与PID控制的仿真结果相比，效果相当，均满足系统的指标要求。

实际工程中，仪表的浮油的黏度受仪表温度的影响较大，当温度升高时，浮油黏度会降低，使仪表的表头参数——绕内框架轴的阻尼系数Cy发生很大的变化，从而影响系统的动态品质和稳定性。本文将系统绕内框架轴的阻尼系数Cy减小20%，再分别对采用PID控制和滑模变结构控制的系统进行仿真，并将系统输出与未改变参数时的系统输出进行对比，如图4所示。

从图4（a）可以看出，采用PID控制算法时，改变参数，系统的超调量由9%变化为40%，振荡次数由0变为2，系统的稳定性变差；而采用滑模变结构控制时，改变参数，系统的超调量由9.8%变化为8.8%，只变化了10.2%，曲线基本重合。这表明，与PID控制相比，滑模变结构控制具有更强的抗参数摄动性。

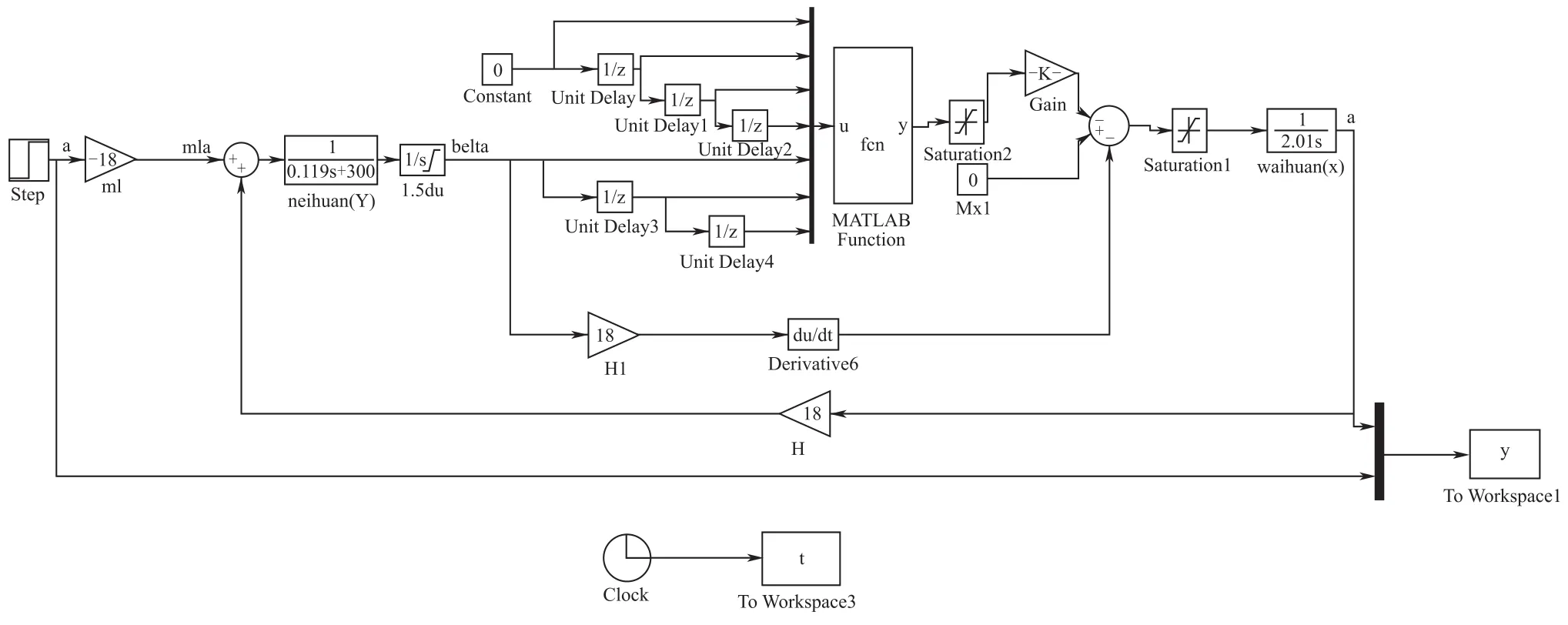
图2　输入为加速度a的系统Simulink仿真图Fig.2 System simulation diagram of input acceleration a

图3　输入为1g的系统输出图Fig.3 System output diagram of input 1g

图4　未改变参数和改变参数后的系统输出对比图Fig.4 System output comparison diagram of original parameters and changed parameters

4　实验

为了验证滑模变结构控制的控制效果，本课题还对上面设计的滑模变结构控制器进行了配表的静态和动态试验，且将其与PID控制的试验结果进行对比。

静态测试为六位置翻滚试验，按照陀螺加速度计的技术条件要求，分别对使用滑模变结构控制和PID控制的伺服电路板进行配表六位置测试。试验结果表明，滑模变结构控制的配表六位置测试的精度符合设计要求，精度与PID控制相当。

六位置翻滚试验是在比较良好的实验室环境下进行的，其系统中的不确定因素比较固定，为了进一步验证变结构控制的优越性，我们后续进行了模拟严苛工作环境的随机振动试验。

随机振动试验采用统一振动功率谱（频率范围为20 Hz～2000Hz，均方根加速度RMS=4.4g0），分别对基于PID控制的伺服回路和基于变结构控制的伺服回路进行配表的随机振动试验，每次振动持续时间为2min，共进行3次，振动中间采集一个静止的输出数据，得到振动精度。然后提高温度，绕内框架轴的阻尼系数Cy发生变化，再分别对基于两种控制策略的伺服回路进行配表的随机振动试验，得到的振动精度如表1所示。

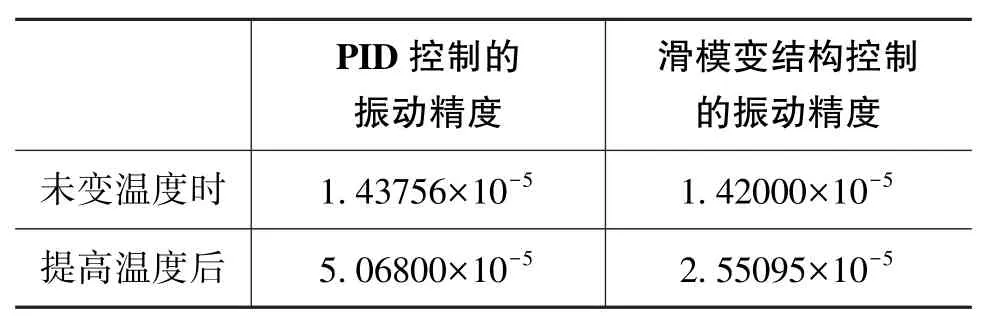
表1　PID控制与变结构控制的配表振动精度对比Table 1 The vibration precision contrast with meter of PID control and variable structure control

由表1可以看出，在本文所述的振动条件下，未改变温度时采用两种控制器得到的振动精度基本相当，而提高温度、改变参数后，滑模变结构控制的振动精度变化幅度为79.64%，而PID控制的变化幅度为252.54%，滑模变结构控制的振动精度稍高。

5　结论

基于数字控制系统，针对陀螺加速度计系统存在着诸如参数摄动等不确定性因素的情况，本文在离散域内设计了一种基于指数趋近律的离散滑模变结构控制器，并通过仿真和实验来验证其正确性。仿真和实验结果表明本文设计的滑模变结构控制器动态品质良好，抗参数摄动性强，具有较好的鲁棒性。

［1］ 严小军，张乐.DSP在陀螺加速度计数字伺服回路中的应用研究［J］.导航与控制，2002，1（1）：44-49. YAN Xiao-jun，ZHANG Le.A research on PIGA's digital servo loop based on DSP［J］.Navigation and Control，2002，1（1）：44-49.

［2］ 高为炳.变结构控制理论及设计方法［M］.北京：科学出版社，1996. GAO Wei-bing.Theory and design method of variable structure control［M］.Beijing：Science Press，1996.

［3］ 陆元九.惯性器件（下）［M］.北京：中国宇航出版社，1990. LU Yuan-jiu.Inertal devices（2nd）［M］.Beijing：China Aerospace Press，1990.

［4］ 于长官.现代控制理论［M］.哈尔滨：哈尔滨工业大学出版社，2006. YU Chang-guan.Modern control theory［M］.Harbin：Harbin Institute of Technology Press，2006.

［5］ 高为炳.离散时间系统的变结构控制［J］.自动化学报，1995，21（2）：154-161. GAO Wei-bing.Variable structure control of discrete-time systems［J］.Acta Automatica Sinica，1995，21（2）：154-161.

［6］ 李伟，韩崇伟，位红军，等.伺服系统的滑模变结构控制器设计［J］.计算机仿真，2011，28（12）：5-13. LI Wei，HAN Chong-wei，WEI Hong-jun，et al.Design of sliding mode controller for servo system［J］.Computer Simulation，2011，28（12）：5-13.

［7］ 刘金琨.滑模变结构控制MATLAB仿真［M］.北京：清华大学出版社，2006. LIU Jin-kun.Sliding mode control of MATLAB simulation ［M］.Beijing：Tsinghua University Press，2006.

［8］ Mija S.J，Thomas Susy.Design of optimal discrete sliding mode controllers［J］.Control and Intelligent Systems？，2012，40（2）：119-124.

［9］ Fang Hong，Bian Xin，Zhou Xin，et al.A design method for automatic calibration system based on dynamic loading and dynamic scheduling［C］.10thInternational Conference on Electronic Measurement&Instruments.Beijing，China，16-19 Aug.2011，2：166-170.

A Studying of Sliding Mode Variable Structure Control for PIGA's Servo Loop

YAN Xiao-hong，YAN Xiao-jun，ZHANG Pei-han，YUE Hui，ZHANG Li-lei
（Beijing Institute of Aerospace Control Devices，Beijing 100039）

Normal working of PIGA requires a corresponding servo loop to ensure that the instrument has sufficient static and dynamic accuracy.This article mainly study the control method of PIGA's servo loop.Based on the digital control system，for a class of uncertain linear problems with parametric perturbation of PIGA’s servo loop，the paper presents a discrete sliding mode variable structure controller，and it's verified by simulation and experiment.The simulation and experiment results show that the sliding mode variable structure controller has good dynamic characteristics，significant anti-interference and strong robustness.

PIGA；servo loop；discrete；sliding mode variable structure control

U666.1

A

1674-5558（2016）02-01089

10.3969/j.issn.1674-5558.2016.03.011

2015-03-17

颜晓虹，女，导航、制导与控制专业，硕士，研究方向为陀螺加速度计伺服回路。