基于体积力模型的1维涡轮特性评估方法

何　杰，邹正平，姚李超

（1.北京航空航天大学航空发动机气动热力国防重点实验室；2.先进航空发动机协同创新中心：北京100191）

基于体积力模型的1维涡轮特性评估方法

何杰1，2，邹正平1，2，姚李超1，2

（1.北京航空航天大学航空发动机气动热力国防重点实验室；2.先进航空发动机协同创新中心：北京100191）

涡轮低维气动特性评估方法的预测精度对涡轮气动设计有重要意义。基于适用于轴流涡轮特性评估的1维体积力方法，分析和局部调整了A dam和Leonard的1维体积力模型中的叶片力源项和离心力源项，并在特性计算中引入涡轮损失模型。通过1个低压涡轮和1个含冷气高压涡轮对该方法进行验证，计算结果表明：该方法对2个算例在涡轮设计工况点的流量效率预测偏差均在1%以内，且能够反映涡轮气动特性随膨胀比的变化趋势，具有良好的精度，可用于快速可靠地评估涡轮低维气动特性。

涡轮；低维设计；体积力模型；欧拉方程；特性评估

0　引言

涡轮部件气动设计是1个从低维到高维逐步设计和优化的过程，低维气动设计是高维空间工作的基础，并在很大程度上决定了涡轮的性能水平，是设计流程中1个非常关键的环节。涡轮低维气动特性评估方法可在涡轮设计初期预测工作特性，其预测精度对涡轮气动设计具有重要意义。

涡轮低维气动特性评估常用方法为1维平均中径法，通过分析涡轮内部气动损失机理并总结损失经验关系式，建立计算轴流涡轮叶栅通道内气动损失的模型，以定量评估涡轮1维平均中径上性能。在工程领域常应用的AMDC损失模型及AMDCKO模型，可较好评估涡轮设计点和非设计点的性能［1-2］。其他比较著名的经验模型如Traupel模型［3］、Craig&Cox模型［4］等也能较好地预测涡轮气动损失。平均中径法在过去应用广泛，但随着涡轮设计技术的发展和设计要求的变化，该方法被用来考虑涡轮中一些新参数的影响规律，如Coull和Hodson等［5］分别分析了流量系数、升力系数和雷诺数等参数对低压涡轮性能的影响规律等；在中国，如姚李超等［6］发展了以载荷系数、反力度、轴向速比等多种设计变量为约束条件求取涡轮效率的多级低压涡轮1维气动优化程序。平均中径法对涡轮性能的预测能力和精度取决于所使用的损失模型精准度和适用范围，对使用者要求较高。

除了平均中径法，利用欧拉方程与体积力相结合对叶轮机性能评估的方法近年来也得到重视，该方法适用于1～3维和非定常等不同维数叶轮机性能的评估。高维体积力模型如Adamcyz提出的通道平均多级流动模型［7］，通过体积力模型来模拟叶片对气流的作用力以求解压气机中的3维流动。高维体积力模型还有其他形式，如适用于3维非定常畸变问题的Gong的周向平均体积力模型［8］和Xu的黏性体积力模型［9］等。低维体积力模型如Adam和Leonard提出的1维模型［10-12］，该模型在低维欧拉方程中引入体积力源项，采用有限体积法求解该方程组从而得到叶轮机流道平均中径上的气动参数，用于确定叶轮机在不同工况下的气动性能，以评估叶轮机械优劣。在此基础上，中科院工程热物理研究所和北京航空航天大学也进行了相应的研究，并发展了多级轴流透平气动特性计算程序［13-14］。

本文在Adam和Leonard的体积力模型的基础上，对1维涡轮特性评估方法进行了研究，分析调整了模型中的叶片力源项和离心力源项，在特性计算中引入了损失模型，通过双级低压涡轮和气冷高压涡轮的性能结果比较对该方法进行验证。

1　计算方法

1.1控制方程

涡轮流道截面如图1所示。本文所建立体积力的源项在空间的分布基于均匀的轴对称特性，在1维评估中只考虑气动参数沿流向的变化，忽略了流道法向气动参数变化，由此建立曲线坐标系（m，n，θ），其中m为流向坐标，n为法向坐标，θ为周向坐标。微元控制体如图2所示。控制体上边界为机匣，下边界为轮毂，假定进口截面为截面①，出口截面为截面②，建立守恒的欧拉微分方程组

其中

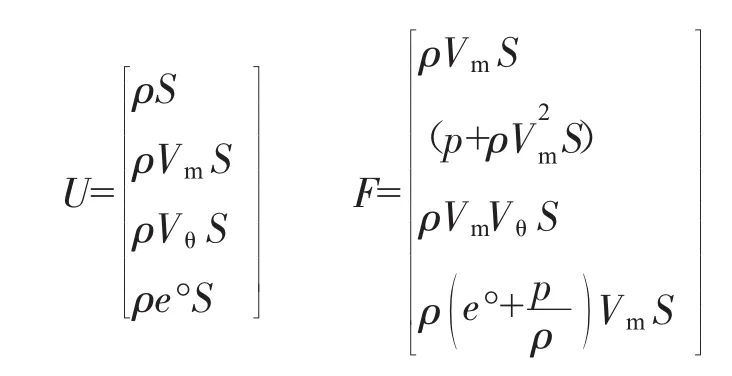
式中：ρ为流体的密度；S为子午流道的横截面积；t为时间；Vm为流体的绝对速度子午流向分量；Vθ为流体的绝对速度周向流向分量；r为到涡轮中心轴线的半径；p为流体的静压；e°为流体的总内能；Qb为无黏叶片力源项；Qf为黏性力源项；Qg为几何力源项；Qc为冷气源项。

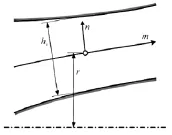
图1　研究坐标　

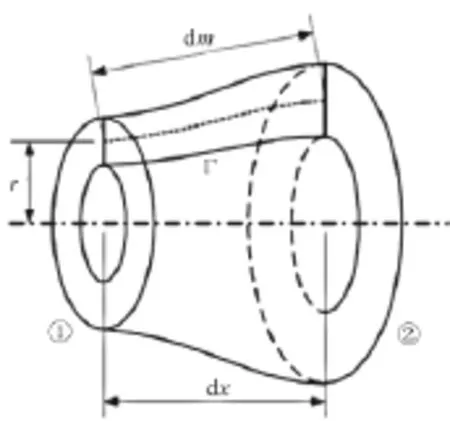
图2　控制体［10］

1.2体积力模型

基于Adam和Leonard的思路［10］，本文局部修正了其体积力模型中无黏叶片力切向分量：体积力模型采取在欧拉方程上添加源项的方法，确定源项对于预测精度和能力至关重要，为了分析源项，给定叶片平均中径进出口速度三角形，其参数如图3所示。

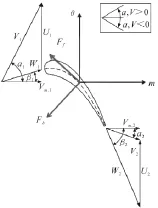
图3　速度三角形

r1、r2分别为叶片进、出口平均中径，对应的周向速度分别为Vθ1、Vθ2，qm为假定通道流量，Vol为叶片排内气体体积。求解源项需要分析叶片黏性力、无黏叶片力、离心力、几何流道形式和冷气影响。

黏性力源项Qf考虑黏性力的影响，作用于叶片区域的黏性力使得流体沿流线产生熵增，利用AMDCKO损失模型求解气流通过叶栅后的熵增Δs，该模型由AMDC损失模型改进得到，不仅适用于低亚声涡轮叶栅，也同样适用于高马赫数的涡轮叶栅。由于叶栅通道几何参数未知，故近似认为气流在叶片区域内的单位流向坐标上的熵增相等，该假设在设计点考虑是合理的［15-16］，在变工况下的熵增分布有待进一步优化改进。从该角度出发，可得黏性力矢量F→f、及其流向分量和周向分量分别为

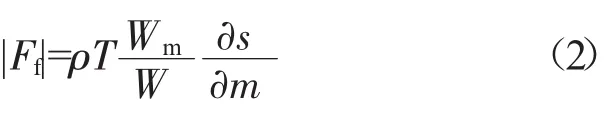
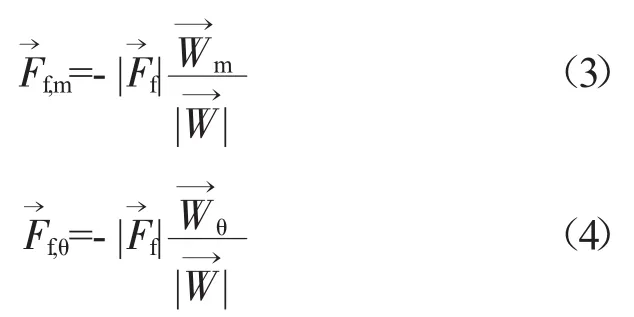
分析动量矩方程的叶片力源项Qb，Adam和Leonard认为动量矩方程中力矩起主导作用的为无黏叶片力力矩［10］，故只考虑无黏叶片力源项。由于涡轮设计工况点流动的主控因素是位势作用，该假设在设计点及设计点附近的状态点是非常合理的，但在1维特性评估过程中，要合理评估非设计状态的性能，在远离设计点的工况下，黏性的影响将越来越大，成为不应被忽略的因素。本文在动量矩方程中将综合考虑无黏叶片力力矩和黏性力力矩的作用，以适用于更宽广的工作范围。利用角动量守恒方程求解切向力总和Fθ，可得单位体积上气体所受到的无黏叶片力切向分量Fb，θ和流向分量Fb，m分别为

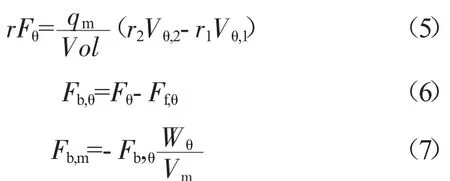
几何力源项Qg包含了离心力和涡轮子午流道形式的影响。Adam和Leonard文献中以轴向为基准坐标，将离心力分解为轴向和周向分量［10］，本文以子午流线为基准坐标，离心率如图4所示。仅考虑叶片旋转引起的离心力，没有离心力周向分量，即离心力只作用在轴向动量方程，不影响切向动量方程。

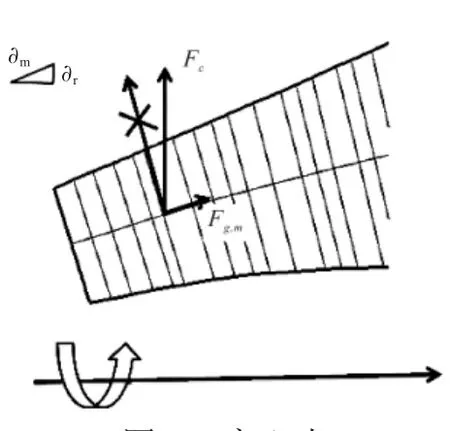
图4　离心力

涡轮子午流道形式指轮毂和机匣之间的流道面积变化，具体为垂直于平均子午流线的横截面面积以及平均中径的变化所带来的影响。

冷气源项Qc主要与冷气有关，本节中所建立的1维体积力模型为简化考虑，只考虑在质量守恒方程和能量守恒方程中添加源项冷气，即冷气的加入会改变通道气体流量和焓的变化，而不影响在流向的动量守恒方程和角动量守恒方程，该假设在冷气量所占比例较小时是合理的。

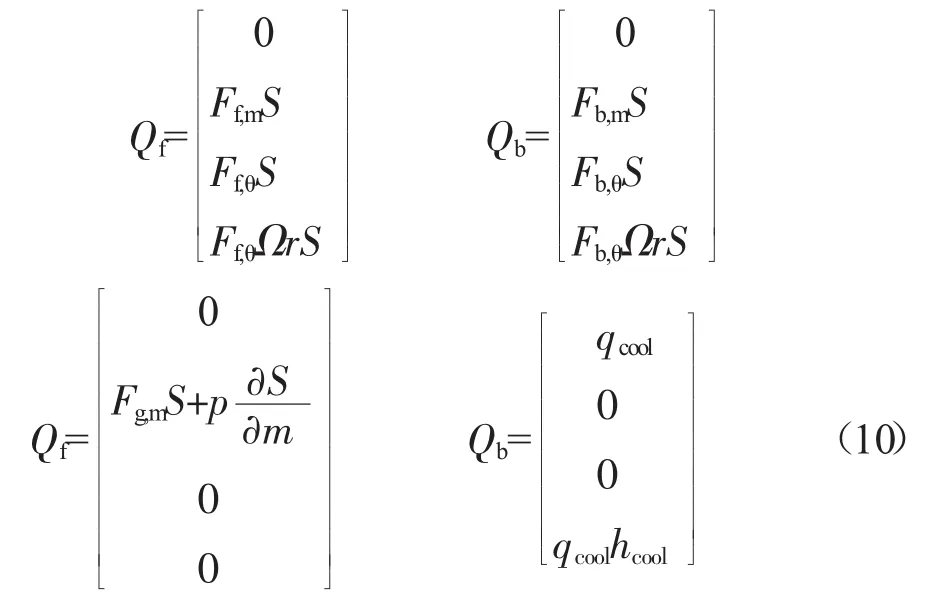
综上所述，各体积力源项分别为

1.3数值方法

采用时间推进的有限体积法求解欧拉控制方程，其数值格式为迎风型矢通量分裂格式AUSM［17］，无黏通量F分裂为对流项和压力项。

程序采用定比热方法计算，计算时需要给出以下条件：涡轮子午面轮毂和机匣型线几何数据、各叶片排前尾缘在子午面内的坐标、各叶片排个数以及进出口几何构造角、冷气参数、涡轮转速以及边界条件。边界条件包括：进口总温和总压、进口切向气流角以及出口静压。在计算过程中通过改变涡轮转速和出口静压以得到涡轮在不同非设计工况下的工作特性。

2　计算结果与讨论

选取2级低压涡轮和冷气单级高压涡轮2个算例涡轮对程序的正确性进行验证，同时与3维RANS计算结果进行对比。

2.12级低压涡轮

某型2级低压涡轮的流道形式如图5所示。涡轮进口总温为1100 K，进口总压为357 kPa，设计转速为11500 r/min，轴向进气、总冷气量较少，小于2%。计算得到不同转速下涡轮流量和效率随膨胀比变化的曲线及其与3维计算结果的对比曲线，如图6所示。

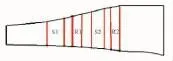
图5　低压涡轮通道

Adam和Leonard的1维模型、修正后的1维模型和3维模型计算的110%，100%、90%、80%折合转速下低压涡轮出口折合流量、效率随膨胀比的变化如图6所示。在流量-膨胀比特性图中，以3维RANS结果为基准，修正后的1维模型比原1维模型对涡轮流量的预测更为精准，对流量堵点出现的位置预测更加精确；在效率-膨胀比特性图中，修正后的1维模型和原1维模型计算结果分别与3维结果对比，修正的1维模型计算结果与3维结果更加贴近。

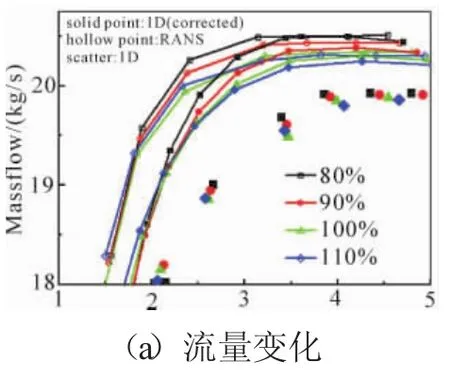
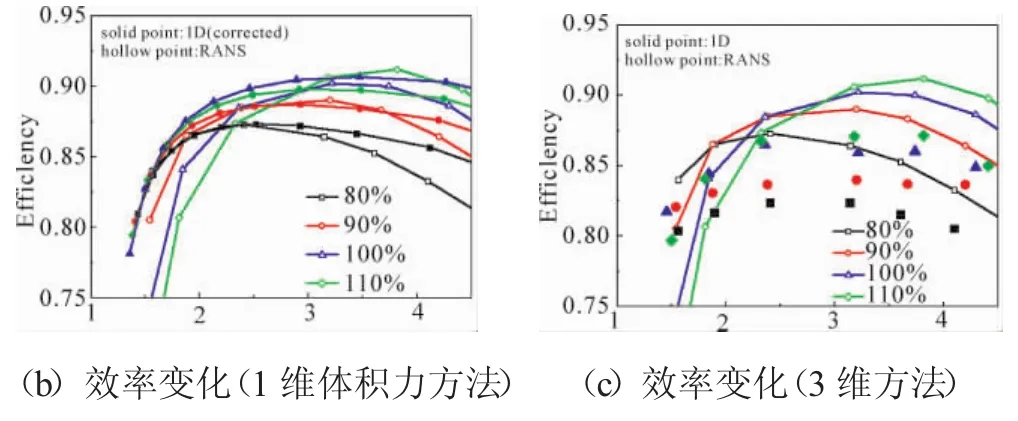
图6　低压涡轮流量、效率随膨胀比和折合转速的变化

修正后的1维体积力模型计算结果与3维RANS计算结果中的涡轮流量和效率的变化趋势基本相同，在不同的折合转速下，利用修正后的1维体积力模型计算的涡轮的流量和效率随着膨胀比的变化特性与3维结果基本相同。

不同转速和膨胀比下的流量和效率偏差如图7所示。对比分析了各状态点的预测精度。流量偏差Δm和效率偏差Δη定义如下

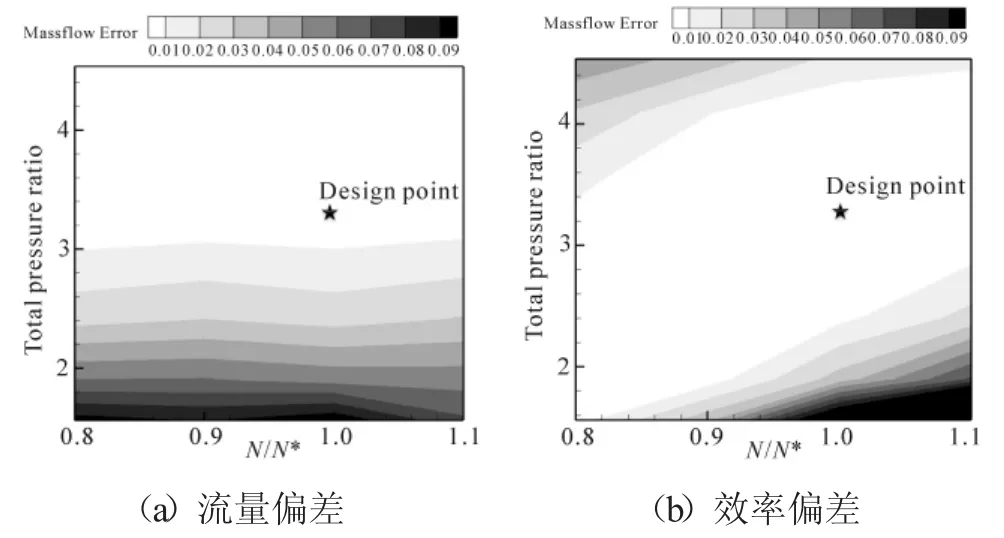
图7　低压涡轮不同转速和膨胀比下的流量和效率偏差

2.2冷气单级高压涡轮

高压涡轮进口总温为1600 K，进口总压为1529 kPa，设计转速为18500 r/min，轴向进气，导叶冷气量为涡轮进口质量流量的10.4%，动叶冷气量为3.8%，该算例中涡轮冷气量较大，应以考核体积力的方法对气冷涡轮性能适应性进行评估。高压涡轮的流道和冷气掺混比例如图8所示。

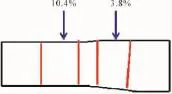
图8　高压涡轮的流道和冷气掺混比例

Adam和Leonard的1维模型、修正后的1维模型和3维计算的100%、90%、80%折合转速下高压涡轮出口折合流量、效率随膨胀比的变化如图9所示。其中冷气涡轮效率定义见文献［18］。从图9（a）中可见，修正后的1维模型计算结果中流量堵塞点出现的位置更符合涡轮真实工作情况，修正后的1维模型的计算结果比原模型的更贴近3维计算结果；从图9 （b）中可见，在膨胀比为4.2的设计点处，修正后的1维体积力模型比原模型对效率的预测更加精确。说明了在不同的折合转速下，采用修正后的1维模型计算的涡轮流量和效率随着膨胀比的变化趋势与3维结果基本相同，修正后的1维模型比原模型对流量特性预测的精度更高。

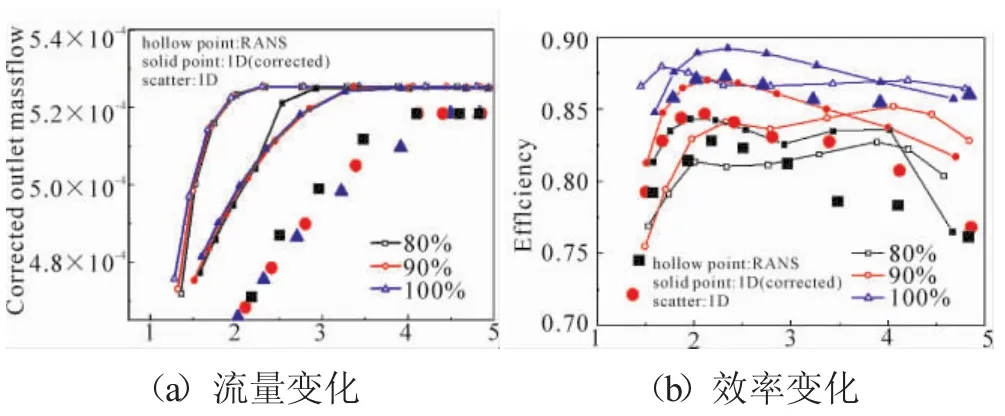
图9　高压涡轮流量和效率随膨胀比和折合转速的变化

高压涡轮不同转速和膨胀比下的流量和效率偏差如图10所示。从图中可见，修正后的1维结果与3维结果的数值偏差较小，设计点处流量偏差和效率偏差均小于1%，非设计点处流量偏差和效率偏差较小，修正后的1维结果可信度较高。针对冷气量较多的高压涡轮，修正后的1维模型仍然可以较为精准地评估涡轮特性。

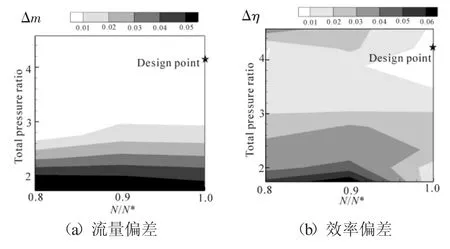
图10　高压涡轮不同转速和膨胀比下的流量和效率偏差

在2个算例中，在偏离设计点状态较远处都出现涡轮流量效率偏差较大的现象，说明体积力模型在非设计点处的预测尚需进一步修正，在非设计点处气动损失模型的精度决定着源项的偏差，对体积力模型的精度有一定影响。如何进一步提高体积力模型在非设计点下的预测精度是未来的工作方向。

3　结论

本文结合修正后的1维体积力模型，改进了计算程序，并对2个算例进行涡轮特性评估，得出以下结论：

（1）修正后的1维体积力模型比原模型对流量特性预测精度更高。能够在设计点处比较准确预测流量效率特性，在非设计点处能够较为准确预测流量特性，且在非设计点处性能偏差在工程允许的误差范围内，能够预测流量效率特性随膨胀比的变化趋势。

（2）低维体积力方法能够快速准确地对涡轮特性进行评估，适用于高压低压、单级多级、含冷气不含冷气的轴流涡轮。

（3）低维体积力方法的预测精度取决于体积力源项的模化，进一步提高体积力模型在涡轮非设计状态下的预测精度是未来的研究方向。

［1］Dunham J，Came P M.Improvements to the Ainley-Mathieson method of turbine performance prediction［J］.Journal of Engineering for Gas Turbines and Power，1970，92（3）：252-256.

［2］Kacker S C，Okapuu U.A mean line prediction method for axial flow turbine efficiency［J］.Journal of Engineering for Gas Turbines and Power，1982，104（1）1：111-119.

［3］TraupelW.Termischeturbomaschinenzweiterbandgeländerte getriebsbe dingungen，regelung，mechanische probleme，temperatur problem ［M］.New York：Springer-Verlag Berlin Heidelberg，1977：73-77.

［4］Craig H R M，Cox H J A.Performance estimation of axial flow turbines ［J］.Proceedings of the Institution of Mechanical Engineers，1970，185 （1）：407-424.

［5］Coull J D，Hodson H P.Blade loading and its application in the Mean-Linedesignoflowpressureturbines［J］.Journalof Turbomachinery，2013，135（2）：21-32.

［6］姚李超，邹正平，张伟昊，等.基于粒子群算法的多级低压涡轮一维气动优化设计方法［J］.推进技术，2013，34（8）：1042-1049.

YAO Lichao，ZOU Zhengping，LIU Huoxing.An optimal method of one-dimensional design for multistage low pressure turbines based on particle swarm optimization［J］.Journal of Propulsion Technology，2013，34（8）：1042-1049.（in Chinese）

［7］Adamczyk J J.Model equation for simulating flows in multistage turbomachinery［J］.Lecture Series-van Kareman Institute for Fluid Dynamics，1996，5（1）：1-28.

［8］Gong Y，Greitzer E M，Tan C S，et al.A computational model for short-wavelength stall inception and development in multi stage compressors［J］.Journal of Turbomachinery，1999，121（4）：726-734.

［9］Xu L.Assessing viscous body forces for unsteady calculations［R］. ASME 2002-GT-30359.

［10］Adam O，Léonard O.A quasi-one dimensional model for axial compressors［R］.ISABE 2005-1011.

［11］Adam O，Léonard O.A quasi-one dimensional model for axial turbines［R］.ISABE 2007-1215.

［12］Adam O，Léonard O.A quasi-one dimensional model for multistage turbomachines［J］.Journal of Thermal Science，2008，17（1）：7-20.

［13］张晓东，刘建军，安柏涛.多级轴流透平气动特性计算方法研究［J］.工程热物理学报，2011，32（4）：569-572.

ZHANG Xiaodong，LIU Jianjun，AN Baitao.Investigation on the computational method of axial turbine aerodynamic characteristics based on 1.5 dimensional Euler equations［J］.Journal of Engineering Thermophysics，2011，32（4）：569-572.（in Chinese）

［14］姚李超.多级低压涡轮低维气动优化设计技术研究［D］.北京：北京航空航天大学，2013.

YAO Lichao.Studies on an optimal method of low dimensional aerodynamic design for multistage low pressure turbine［D］.Beijing：Beihang University，2013.（in Chinese）

［15］Damle S V，Dang T Q，Reddy D R.Through flow method for turbomachinesapplicableforallflow regimes［J］.Journalof Turbomachinery，1997 119（2）：256-262.

［16］郑宁，邹正平，徐力平.风扇进气畸变三维非定常数值模拟技术研究［J］.航空动力学报，2007，22（1）：60-65.

ZHENG Ning，ZOU Zhengping，XU Liping.3D Unsteady numerical simulation of fan/compressor with inlet distortion［J］.Journal of Aerospace Power，2007，22（1）：60-65.（in Chinese）

［17］Liou M S.A sequel to ausm：ausm+［J］.Journal of Computational Physics，1996，129（2）：364-382.

［18］Hartsel J E.Prediction of effects of mass-transfer cooling on the blade-row efficiency of turbine airfoils［C］//AIAA 10th Aerospace Sciences Meeting，San Diego：AIAA Paper，1972：17-19.

（编辑：赵明菁）

A One-Dimensional Simulation Method to Evaluate Turbine Performance Based on Body Forced Model

HE Jie1，2，ZOU Zheng-ping1，2，YAO Li-chao1，2
（1.National Key Laboratory of Science and Technology on Aero-engines,Beihang University；2.Collaborative Innovation Center of Advanced Aero-engine：Beijing 100191,China）

The precision of turbine aerodynamic performance of low dimensional evaluation method is of great significance for the turbine aerodynamic design.A one-dimensional simulation method for axial flow turbine based on body force model was studied，the blade force source term and centrifugal force source term in Adam and Leonard body force model were corrected，the turbine loss models were introduced in the computation.The method was verified by a low pressure turbine and an air cooling high pressure turbine，and the results show that efficiency deviation of two examples turbine at design point is within 1%.In addition，the results can reflect the tendency for aerodynamic performance of the turbine with the expansion ratio variation.All in all，the corrected body force model has a good precision，and can be used as a fast and reliable evaluation method of low dimensional gas turbine performance.

turbine；low dimensional design space；body force model；Euler equation；performance evalution

V 211.6

A

10.13477/j.cnki.aeroengine.2016.02.005

2015-08-05

何杰（1993），男，在读硕士研究生，研究方向为叶轮机械数值仿真；E-mail：hejie@buaa.edu.cn。

引用格式：何杰，邹正平，姚李超.基于体积力模型的1维涡轮特性评估方法［J］.航空发动机，2016，42（2）：22-26.HE Jie，ZOUZhengping，YAOLichao.A one-dimensionalsimulationmethodtoevaluateturbineperformancebasedonbodyforcedmodel［J］.Aeroengine，2016，42（2）：22-26.