基于paillier的隐私保护下关联规则挖掘方法

2016-09-22邢欢张琳

网络与信息安全学报 2016年1期

关键词：同态项集数据挖掘

邢欢，张琳

（南京邮电大学计算机学院，江苏南京 210003）

基于paillier的隐私保护下关联规则挖掘方法

邢欢，张琳

（南京邮电大学计算机学院，江苏南京 210003）

在基于隐私保护的数据挖掘中，挖掘的精度和安全性一直是一对矛盾，针对该矛盾提出了一种在分布式的环境下基于paillier同态加密的关联规则挖掘方法，该方法将计算方和解密方分离保证了数据挖掘的安全性，同时基于同态加密并不会影响挖掘的精度，并通过蒙哥马利算法降低了paillier算法的开销，经过实验发现在增加加解密过程后算法开销还是在能接受的范畴内。

隐私保护；关联规则；同态加密

1　引言

目前在大数据的浪潮下促进了一大群学者针对数据挖掘进行研究，然而在数据的挖掘过程中，隐私保护的问题日益突出。当年啤酒尿布的经典案例引发了人们对于关联规则挖掘的兴趣。而关联规则挖掘也正是数据挖掘中十分重要的一个领域，关联规则挖掘算法如Apriori算法、FP增长算法等经过多年的研究和改进已比较成熟。然而在如今的信息时代，关联规则挖掘早已不再是单方的数据挖掘，正是由于多方数据挖掘，隐私保护也越显重要。关联规则挖掘存在的隐私保护问题主要有如下两种情况：数据提供方并不是关联规则挖掘方，所以数据提供方希望在挖掘出正确结果的同时并不会泄露提供数据中的隐私内容；另一种情况主要是多个数据提供方想要共同进行数据挖掘，然而多方之间也不想泄露隐私数据信息。针对以上的隐私保护问题，已经有很多学者提出了相关的协议以及算法。文献［1，2］提出了基于差分隐私的算法，差分隐私保护最大的优点是与背景知识无关，然而差分隐私保护却不可避免数据失真，改进也只是将失真程度减小到最低。文献［3］利用随机响应技术，在概率的基础上对数据进行挖掘，虽然在数据挖掘的准确性和安全性方面做了很好的平衡，但也无法完美地解决这两方面之间的问题。文献［4］基于 FDM（fast distributedmining of association rules）算法提出了针对上述第2种情况下频繁项集挖掘的协议以及算法。文献［5，6］都提出了基于遗传算法的隐私保护下的关联规则挖掘算法，然而算法在挖掘精度方面并不完美。文献［7］提出了一种基于重构数据分布和添加数据干扰实现隐私保护下关联规则的挖掘算法，但同时由于数据的干扰也导致了数据属性的相关性遭到破坏，数据挖掘精度不够。文献［8］针对多方进行频繁项集挖掘时存在恶意挖掘其他方信息的情况，提出了一种新的算法，但是算法开销稍高。文献［9］根据不同的安全等级设置相应的数据干扰来实现数据挖掘中的隐私保护。文献［10］提出了一种基于FDM的水平分布式协议，具有较好的通信效率和安全性。文献［11］针对多方协作数据挖掘隐私泄露问题提出了一种二进制整数规划模型。文献［12］针对两方协作关联规则挖掘提出了基于可交换加密的协议。文献［13］提出了一种基于泛化实现隐私保护的算法，然而使用泛化不可避免地使数据挖掘的精度受到影响。

在基于隐私保护的关联规则挖掘中往往数据挖掘的安全性和挖掘精度是一对矛盾。在使用同态加密的情况下，关联规则挖掘的过程既能保证数据的安全性又能保证数据挖掘的精度。唯一的不足是算法开销稍高，然而如今最重要的问题是数据挖掘的精度和安全性、算法和技术的改进以及硬件设备的提升，而算法所需的时间消耗相对没有数据挖掘精度和安全性那么重要。因此，本文提出了一种基于paillier同态加密的关联规则挖掘方法。

2　相关定义

2.1关联规则

事务集为D，项集集合为I，事务t∈T由I中元素组成，支持数是项集A在事务集D中的计数|A|，支持度是项集A的支持数在事务集中的比例最小支持度为minsup，若则A是频繁项集。关联规则是形如AB⇒的表达式，A是规则前件，B是规则后件。置信度是指项集A和项集B的支持度与项集A的支持度的比值

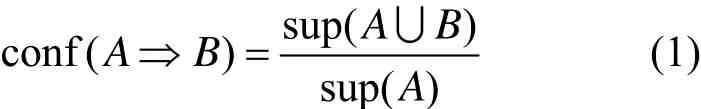
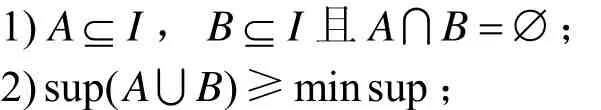
2.2Paillier同态加密算法

Paillier是基于合数阶剩余类的概率公钥密码系统，其理论安全性构建在比“RSA假设”更强的“CCRA假设”上。Paillier加密算法具有加法同态和混合乘法同态的特性。在涉及到多方关联规则挖掘时，由于各方都不希望泄露自身的数据，所以可以将项集的支持数等数据特征进行加密。关联规则挖掘的关键在于频繁项集的挖掘，也就是全局支持数的计算。因此关键在于累加各方的项集支持数，而计算过程不应泄露数据信息，所以可以利用paillier加密算法的加法同态特性。

Paillier加密算法的加密过程为

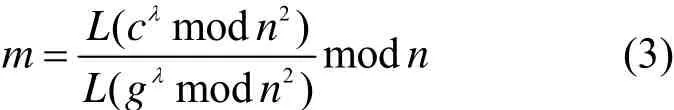
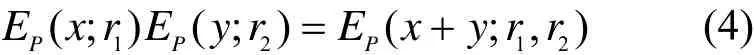
3　算法描述

3.1多方参与的关联规则挖掘方案

问题：存在多个数据提供方，在不泄露自身隐私数据的条件下共同挖掘关联规则。

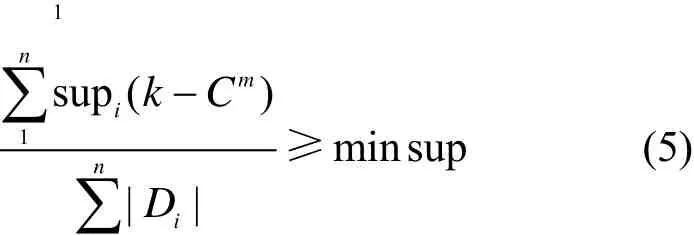
则将候选k项集 k - Cm添加到频繁k项集k -L中。由式（5）得到

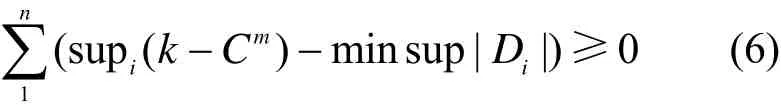
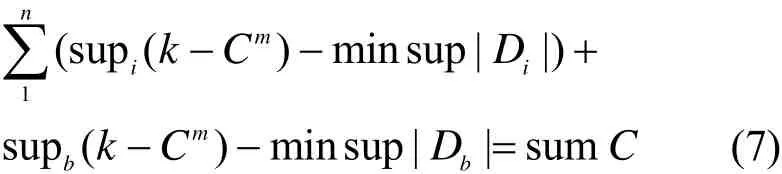
通过上述方法即可安全挖掘多方频繁项集，在已有频繁项集的基础上再通过ap-genrules产生关联规则，为方便描述，将关联规则用A B⇒ 表示，而判断该关联规则是否是所需要的还需要进行最关键的一步计算：min conf是全局最小置信度阈值。

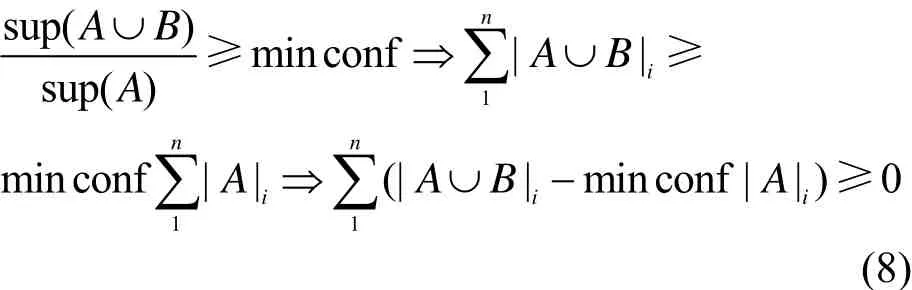
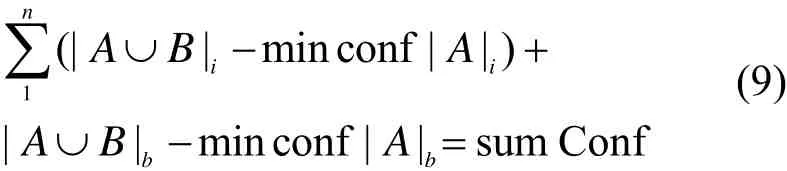
Pa将和的使用文献［14］的方法进行比较，若则有趣的关联规则。频繁项集挖掘和关联规则挖掘过程中的主要流程相同，如图1所示。

3.2计算优化

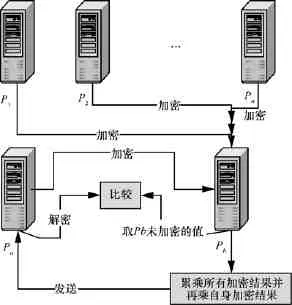
图1　多方规则挖掘时的同态加解密过程

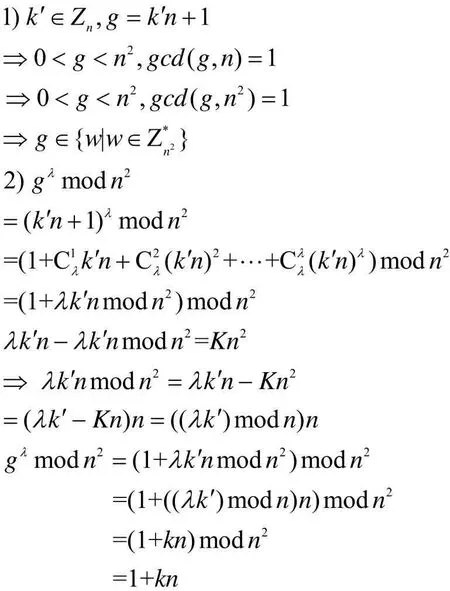
步骤4重复步骤3和步骤4直到m=0， returnD。

算法流程如图2所示，加解密过程中的模幂运算全部转化为模乘运算，实验显示使用蒙哥马利算法能将计算时间降到极低的标准，使paillier同态加密算法的开销达到令人满意的程度。

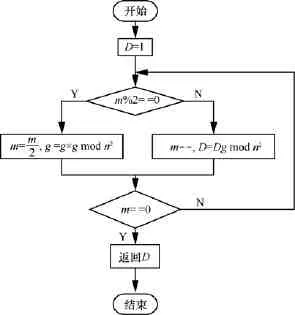
图2　模幂运算转化成模乘运算

4　算法设计

4.1频繁项集挖掘算法

1）每个数据提供方 Pi由Apriori-gen算法根据全局k-1-频繁项集得到本地候选k-频繁项集的集合并由本地支持数剪枝得到

2）Pi公布自己的获得对中每个项集计算使用公钥对（g， z）加密，其中，和q是大素数，对其加密得到并将加密结果发送给 Pb。

3）Pb计算通过公钥对加密得到再计算并将结果发送给 Pa。

4）Pa根据解密得到其中

5）使用文献［8］百万富翁问题中使用的部分标量积保密计算方法比较 Pa的sumC和 Pb的如果将添加到

6）频繁1项集的获取由

iP根据局部最小支持度minsupi得到局部候选1项集再循环第3）步至第5）步得到频繁1项集的集合1L-。

4.2关联规则挖掘算法

1）针对每一个频繁k项集，使用ap-genrules算法产生候选关联规则每个数据提供方使用公钥对（g， z）对加密，并将加密结果发给Pb。

2）Pb并将结果再发给aP。

3）Pa通过私钥λ解密得到Pa将和的使用文献［8］的方法进行比较，若则是有趣的关联规则。

5　仿真实验

本文的方法基于同态加密技术，在关联规则挖掘前并没有更改数据集，所以并不会影响关联规则挖掘的结果。本文方法的安全性是基于paillier加密算法的，paillier算法的安全性不弱于“RSA假设”，并且paillier加密算法是语义安全的，即不存在任何多项式时间算法能够区分不同值的加密结果。所以，本文的关联规则挖掘的安全性和挖掘精度问题都是能够保障的。主要通过实验来测试本文算法开销。

实验是由100个项组成的项集和10 000条事务。将10 000条事务分成5组，相当于每个数据方有2 000条数据。即仿真5个数据方在隐私保护的前提下共同挖掘关联规则。算法最主要的消耗在于加解密过程，本文对不同秘钥长度下paillier加密时间与本文改进了paillier的加解密计算过程之后的加密时间进行对比。不同秘钥位数的算法开销对比如图3所示。其中密钥长度为：16、32、64、128、256、512、1024、2048。而当密钥长度大于1 024时，安全性就相当高，从图3可以看出本文方法在密钥长度大于1 024时，加密时间能节省100 ms以上，而在关联规则挖掘过程中，频繁项集的挖掘都是呈指数增长的，所以本文方法有较大优势。

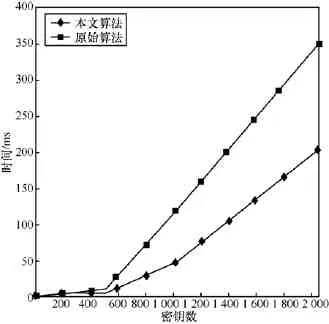
图3　不同秘钥数的算法开销对比

在关联规则的挖掘精度、安全性以及算法开销上，本文基于paillier同态加密的算法与文献［5］在分布式环境下基于遗传算法的关联规则挖掘算法以及文献［3］的使用随机响应技术的经典算法进行了对比。在上述介绍的实验环境下对3种方法进行对比，为方便描述，将文献［5］的算法记为GADM算法，将文献［3］算法记为RRDM算法。实验首先将10 000条事务在5组不同的最小支持度和最小置信度阈值下使用Apriori算法进行关联规则挖掘，这5组值如表1所示。然后分别使用本文算法、GADM算法以及RRDM算法在这5组最小支持度和最小置信度阈值下进行挖掘，其中规则准确率比较结果如图4所示。显然GADM和RRDM规则挖掘的准确率并不是很完美，而由于本文使用了加密解密的形式，并不会影响最后规则的挖掘。3种算法的时间消耗对比如图5所示，其中本文算法分别使用512 bit、1024 bit、2048 bit密钥进行对比。

表1　测试数据

图4　规则准确率对比

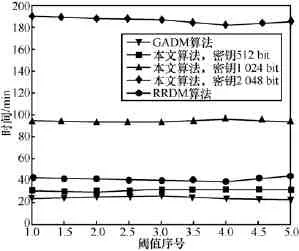
图5　在使用不同秘钥时的时间对比

由此可见，当密钥数为512时，与GADM算法消耗相比是可接受的。其中RRDM是矩阵计算，矩阵规模大算法开销同样巨大，而且基于随机响应的方法存在一定的概率把扰乱后的数据还原，所以安全性并不高。然而本文算法在挖掘的精度和安全性方面却比GADM算法和RRDM算法有较大优势。

6　结束语

目前针对数据挖掘的隐私保护已经有了很多研究，但是数据挖掘的精度和数据挖掘过程中的安全性一直是一对矛盾。本文提出了一种基于paillier同态加密的能够实现隐私保护关联规则挖掘方法，能很好地解决挖掘精度和安全性问题，虽然增加了加解密过程，但是通过蒙哥马利算法提高了加解密性能，最终实验显示算法消耗还是可接受的。并且本文使用的

paillier加密算法的安全性是建立在比“RSA假设”更强的“CCRA假设”上，所以相比于其他多方安全计算中涉及到的加密算法更安全。但是本文方法的算法开销稍大，这是以后需要继续深入研究的内容。

［1］丁丽萍，卢国庆.面向频繁模式挖掘的差分隐私保护综述［J］.通信学报，2014，35（10）：200-209.DING L P，LU G Q.Survey of differential privacy in frequent pattern mining［J］.Journal on Communication，2014，35（10）：200-209.

［2］张啸剑，孟小峰.面向数据发布和分析的差分隐私保护［J］.计算机学报，2014，37（4）：927-949.ZHANG X F，MENG X F.Differential privacy in data publication and analysis［J］.Chinese Journal of Computers，2014，37（4）：927-949.

［3］SUN C J，FU Y，ZHOU J L，et al.Personalized privacy-preserving frequentitemsetmining using randomized response［J］.The Scientific World Journal，2014（3）：686151.

［4］ TASSA T.Secure mining of association rules in horizontally distributed databases［J］.IEEE Transactions on Knowledge and Data Engineering，2014，26（4）：970-983.

［5］KESHAVAMURTHY B H，KHAN A M，TOSHNIWAL D.Privacy preserving association rule mining over distributed databases using genetic algorithm［J］.Neural Comput&Applic，2013，22（1）：351-364.

［6］ LIN C W，ZHANG B B，YANG K T，et al.Efficiently hiding sensitive itemsets with transaction deletion based on geneticalgorithms［J］.The Scientific World Journal，2014：398269.

［7］ANEKRITMONGKOL S，KASEMSAN K.SQL model in language encapsulation and compression technique for association rules mining［J］.International Journal of Intellectual Property Management，2013，4（1）：65-75.

［8］SEKHAVAT Y A，FATHIAN M.Mining frequent itemsets in the presence of malicious participants［J］.The Institution of Engineering and Technology，2010，4（2）：80-92.

［9］ LI Y P，CHEN M H，LI Q W，et al.Enabling multilevel trust in privacy preserving data mining［J］.IEEE Transactions on Knowledge and Data Engineering，2012，24（9）：1598-1612.

［10］TASSA T.Secure mining of association rules in horizontally distributed databases［J］.IEEE Transactions on Knowledge and Data Engineering，2014，26（4）：970-983.

［11］BHANUMATHI S，SAKTHIVEL A.A new model for privacy preserving multiparty collaborative data mining［C］//International Conference on Circuits，Power and Computing Technologies.c2013：845-850.

［12］ZHANG F，RONG C M，ZHAO G，et al.Privacy-preserving two-party distributed association rules mining on horizontally partitioned data［C］//International Conference on Cloud Computing and Big Data.c2013：633-640.

［13］HAJIAN S， DOMINGO-FERRER J， FARRÀS O.Generalization-based privacy preservation and discrimination prevention in data publishing and mining［J］.Data Mining& Knowledge Discovery，2014，28：1158-1188.

［14］李顺东，王道顺.基于同态加密的高效多方保密计算［J］.电子

学报，2013，41（4）：798-803.

LI S D，WANG D S.Efficient secure multiparty computation based on homomorphic encryption［J］.Acta Electronica Sinica，2013，41（4）：798-803.

Privacy-preserving mining of association rules based on paillier encryption algorithm

XING Huan，ZHANG Lin

（College of Computer，Nanjing University of Posts and Telecommunications，Nanjing 210003，China）

In privacy preserving association rule mining，the precision and security of mining are always a pair of contradictions.A method of privacy-preserving mining of association rules based on paillier encryption algorithm over distributed databases was proposed.The method separated calculation and decryption so it can solve the problem of accuracy and security from mining of association rules perfectly.The method can reduce the time cost by Montgomery reduction.The experiment shows that the time cost on the basis of adding the process of encryption and decryption is acceptable.

privacy preserving，association rules，homomorphic encryption

TP311

10.11959/j.issn.2096-109x.2016.00014

2015-10-19；

2015-12-30。通信作者：张琳，zhangl@niupt.edu.cn

国家自然科学基金资助项目（No.61402241）；江苏省自然科学基金资助项目（No.BK2012436）；省属高校自然科学研究重大基金资助项目（No.12KJA520002，No.14KJA520002）；江苏省高校自然科学基金资助项目（No.13KJB520017）

Foundation Items:The National Natural Science Foundation of China（No.61402241），The Natural Science Foundation of Jiangsu Province（No.BK2012436），Natural Science Key Fund for Colleges and Universities of Jiangsu Province（No.12KJA520002 No.14KJA520002），TheNaturalScienceFundforCollegesandUniversitiesofJiangsuProvince（No.13KJB520017）