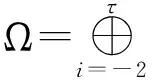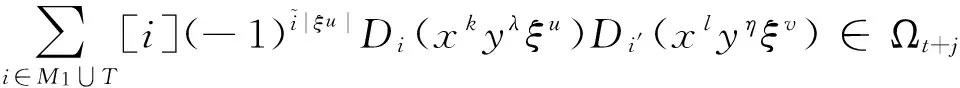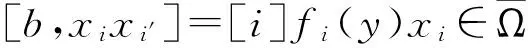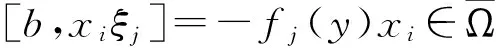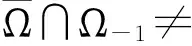Ω-型模李超代数的阶化
2016-09-22徐晓宁
徐晓宁,王 瑾
(辽宁大学数学学院,辽宁 沈阳 110036)
Ω-型模李超代数的阶化
徐晓宁,王瑾
(辽宁大学数学学院,辽宁 沈阳 110036)
证明了模李超代数Ω是Z-阶化的李超代数.利用Ω的Z-阶化,确定了模李超代数Ω的极大子代数,证明了Ω0在Ω-1上的表示是不可约的.
模李超代数;阶化;表示
1 Ω的定义
模李超代数的确定起步较晚,但也已经取得了颇多成果.[1-7]文献[8]利用截头多项式代数与Grassmann超代数做张量积,得到了一篇有限维单模李超代数Ω,即Ω-型模李超代数,给出了其导子超代数,并证明了其与已知的Cartan型模李超代数都不同构.文献[9-10]分别讨论了有限维与无限维Ω-型模李超代数的滤过不变性.文献[11]研究了Ω-型模李超代数的二阶上同调.文献[12]讨论了Ω-型模李超代数的偶部.文献[13]确定了Ω-型模李超代数的偶部到奇部的具有负Z-次数的导子.文献[14]确定了Ω-型模李超代数的结合型与限制性.文献[15]研究了无限维Ω-型模李超代数的超导子代数.
本文讨论Ω-型模李超代数的阶化.利用Z-阶化,确定了Ω-型模李超代数的极大子代数及Ω0在Ω-1上表示的不可约性.

记N与N0分别是自然数集与非负整数集.设n∈N,r=2n+2,令μ1,…,μr-1∈F,且满足μ1=0,μj+μn+j=1,j=2,…,n+1.置M={1,…,r-1},s=r+q,T={r+1,…,s}.令si∈N0,i=1,…,r-1,定义截头多项式代数
A=F[x10,x11,…,x1s1,…,xr-10,xr-11,…,xr-1sr-1,y1,…,ym],
使得





Bk={〈i1,i2,…,ik〉|r+1≤i1 若2≤i≤n+1,则令i′=i+n与[i]=1;若n+2≤i≤r-1,则令i′=i-n与[i]=-1;若i∈T,则令i′=i与[i]=1. 命题2.1设i∈Z,令 证明对于任意的t,j∈Z,令xkyλξu∈Ωt,则 令xlyηξv∈Ωj,则 直接计算得 因为xk-e1xlyλ+ηξuξv的Z-次数为 所以xk-e1xlyλ+ηξuξv∈Ωt+j.类似地, 注意到 由于xk-eixl-ei′yλ+ηξuξv的Z-次数为 且xkxlyλ+ηDi(ξu)Di(ξv)的Z-次数也为 故 命题2.2设ρ:Ω0→pl(Ω-1)是Ω0在Ω-1上的表示,则ρ不可约. 证明设M是Ω-1的非零子模,且 设存在某个i使得fi(y)≠0,则 b=[a,xixi′]=[i]fi(y)xi∈M. d=[x1,xih(y)]=α1(1-ui-λ1)xiyλ1+α2(1-ui-λ2)xiyλ2+…∈M, 从而 (ui′-λ1)xih(y)-d=α2(λ2-λ1)xiyλ2+…∈M, 其所含元素个数比xih(y)中所含元素个数少,矛盾.故M只含有一个元素xiyλ.对任意的η∈H,有 xiyλ=[i][xiyλ,xixi′yη-λ]∈M. 对于任意的η∈H,j∈M∪T,有 xjyη=[i][xiyη,xi′xj]∈M,ξjyη=[i][xiyη,xi′ξj]∈M. 所以M=Ω-1.结论得证. 若f0(y)=0,则b∈Ω-1.设f0(z)≠0,有: [1]PETROGRADSKI V M.Identities in the enveloping algebras of modular Lie superalgebras[J].Algebra,1992,145:1-21. [2]LEITES D.Towards classification of simple finite dimensional modular Lie superalgebras in characteristicp[J].Prime Res Math,2007,3:101-110. [3]ZHANG Y Z.Finite-dimensional Lie superalgebra of Cartan type over fields of prime characteristic[J].Chin Sci Bull,1997,42:720-724. [4]SHU B,ZHANG C.Restricted representations of Witt superalgebras[J].Algebra,2010,324:652-672. [5]FU J Y,ZHANG Q C,JIANG C B.The Cartan-type modular Lie superalgebraKO[J].Comm Algebra,2006,34(1):107-128. [6]LIU W D,ZHANG Y Z,WANG X L.The derivation algebra of the Cartan-type Lie superalgebraHO[J].J Algebra,2004,273:176-205. [7]张永正,刘文德.模李超代数[M].北京:科学出版社,2004,191:1-25. [8]ZHANG Y Z,ZHANG Q C.Finite-dimensional modular Lie superalgebra Ω[J].J Algebra,2009,321:3601-3619. [9]XU X N,CHEN L Y,ZHANG Y Z.On the modular Lie superalgebra Ω[J].J Pure Appl Algebra,2011,215:1093-1101. [10]XU X N,MU B.Infinite-dimensional modular Lie superalgebra Ω[J/OL].Abstr Appl Anal,2013[2015-06-01].http://dx.doi.org/10.1155/2013/923101. [11]XU X N,LI X J.Second cohomology of the modular Lie superalgebra Ω[J].Hacet J Math Stat,2014,43(5):787-799. [13]徐晓宁,卢亚男.关于Ω-型模李超代数[J].数学杂志,2015,35(3):643-655. [14]徐晓宁,张朝凤,张永正.模李超代数Ω的结合型与限制性[J].东北师大学报(自然科学版),2009,41(1):1-5. [15]李明,徐晓宁.无限维模李超代数Ω的超导子代数[J].东北师大学报(自然科学版),2014,46(3):7-11. (责任编辑:李亚军) The gradation of modular Lie superalgebra of Ω-type XU Xiao-ning,WANG Jin (School of Mathematics,Liaoning University,Shenyang 110036,China) It is proved that modular Lie superalgebra Ω isZ-graded Lie superalgebra.By using theZ-graded of Ω,a maximal subalgebra of Ω is determined.And it is shown that the representation of Ω0on Ω-1is irreducible. modular Lie superalgebras;gradation;representation 1000-1832(2016)03-0001-04 2015-06-01 国家自然科学基金资助项目(11371182,11501274);辽宁大学申请国家预资助项目(2014LDGY01);辽宁省教育厅科学研究项目(L2015203). 徐晓宁(1976—),女,教授,主要从事李理论研究. O 152.5[学科代码]110·2130 A [DOI]10.16163/j.cnki.22-1123/n.2016.03.001






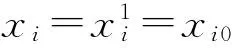
2 Ω的Z-阶化