无人车导航路径关键点插值算法

陆　峰，章永进，李　鹏，赵　明

(1.军事交通学院 研究生管理大队，天津 300161； 2.军事交通学院 军用车辆系，天津 300161；3.军事交通学院 联合投送系，天津 300161； 4.96819部队，北京 100088)



无人车导航路径关键点插值算法

陆峰1，章永进2，李鹏3，赵明4

(1.军事交通学院 研究生管理大队，天津 300161； 2.军事交通学院 军用车辆系，天津 300161；3.军事交通学院 联合投送系，天津 300161； 4.96819部队，北京 100088)

为解决无人车导航路径关键点插值问题，利用Catmull-Rom样条插值方法对关键点插值算法进行研究。在分析Catmull-Rom样条插值算法原理的基础上进行编程，并综合考虑比较B样条插值和三次样条插值方法的优缺点，提出利用Catmull-Rom样条插值方法对关键点进行插值。经验证，该插值方法使插值曲线经过关键点，且插值算法不受坐标分布的影响，并对提供的点坐标的排列没有严格要求，能够满足无人车路径选择的需要。

插值算法；导航路径关键点；无人驾驶汽车

无人车要实现自主导航，可利用的地图有两种，一种是使用精确地图，即利用精确专业的地图规划路线，得到无人车行驶的关键点。但这种方法需要制作精确专业的地图，其制作和使用的成本较高。另一种方法就是利用现有的地图，获取地图规划的关键点，然后针对这些关键点进行插值，以提供给无人车使用。

百度地图应用程序界面(application program interface，API)技术能够为我们提供方便快捷的路径导航检索功能。百度地图依据给定的起点终点的名称、坐标等信息，可以较为迅速地由路网规划出用户所需的线路。通过调用百度地图API技术，及时获取规划路线上关键点的信息，包括它的百度坐标等，这对无人车的驾驶导航有很大的帮助。但是，通过实践发现，调用百度地图API获取的关键点较为稀疏，通常是几十米或几百米才有一个定位点，即其提供的道路点很少。而无人车对导航的要求约0.5 m一个点，因此，点的数量远远不能保证无人车的正常行驶。

通过对百度地图API提供的关键点进行插值，使关键点变多、变密，满足无人车导航的要求，是无人车研究中的一个重要问题。插值算法必须要满足：第一，插值算法效率一定要高，否则会对车辆的导航和行驶造成很大的影响；第二，插值算法必须能满足各种点的插值，不受坐标分布的影响；第三，考虑到不在车道上的关键点对无人车来说是无效的，插值算法还要求能经过所给定的关键点。

为了解决这个问题，人们已经提出了许多种样条插值方法。如Bravo等[1]提出了β样条插值方法；Berglund等[2]提出了将贝塞尔曲线引用至路径规划中；王幼民等[3-4]做了B样条曲线轨迹优化的研究；Shizizu等[5]提出了利用回旋曲线进行轨迹优化的研究；文献[6]在机器人轨迹生成算法中利用了三次样条插值算法。这些方案在无人车导航路径插值计算中能够满足一定程度的利用，但其应用范围仍然有限。贝塞尔曲线虽然能使关键点形成圆滑的曲线，但有一定的弊端：一方面，特征多边形顶点数决定了它的阶次数，当顶点数较大时，不仅计算量增大，稳定性降低，且控制顶点对曲线的形状控制减弱；另一方面，不具有局部性，即修改一个控制点对曲线产生全局性影响。针对以上弊端，1972年Gordon等用B样条基函数代替Bernstein基函数，从而改进上述缺点。尽管它能使关键点通过插值形成圆滑的曲线，不受坐标分布的影响，且效率高，但其不能通过关键点，这会导致路径规划失效[7]。三次样条插值能较好地在通过关键点的情况下拟合成圆滑的曲线，但其形成的原理对关键点的坐标提出较高的要求，很难得到广泛的应用[8-9]。

本文在宏观的路线规划基础上，综合学习比较各种插值方法，引入了Catmull-Rom样条插值方法，使宏观规划出的关键点得到细化，能够供无人车导航决策使用[10]。

1　样条插值算法的分析

1.1B样条曲线的分析

第i段n次B样条曲线的数学表达式为

(1)

式中：Pi,n(u)为n次B样条插值曲线函数；Pi+k为插值点；Nk,n(u)为n次B样条基函数，也称B样条分段混合函数。

在式(1)中，0≤u≤1；i=0,1,…，m，故可以看出B样条曲线是分段定义的。如给定m+n+1个顶点Pi(i=0,1，…，m+n)，则可定义m+1段n次的参数曲线。

Nk,n(u)的表达式为

(2)

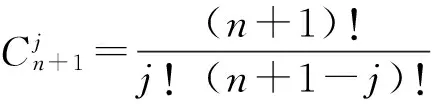
B样条曲线的优点是修改某一控制点只引起与该控制点相邻的曲线形状发生变化，远处的曲线形状不受影响。其特点包括严格的凸包性、分段参数多项式、可微性或连续性、几何不变性、局部可调性、变差缩减性等。这些优点使得B样条曲线广泛应用于交互式自由曲面设计。

1.2三次样条曲线的分析

三次样条曲线S(x)是一个分段定义的公式。给定n+1个数据点，共有n个区间。假设有以下节点：

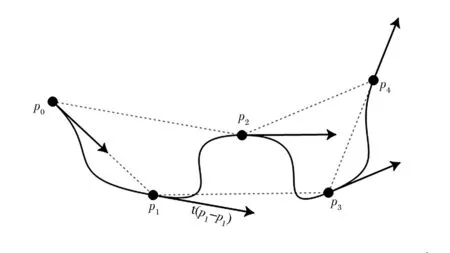
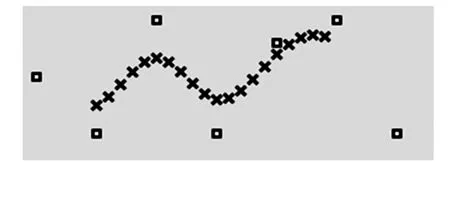
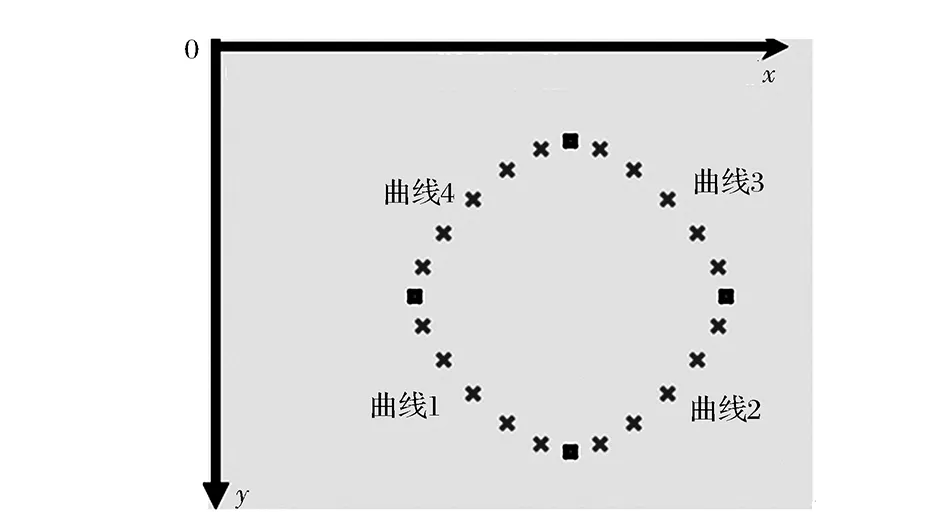
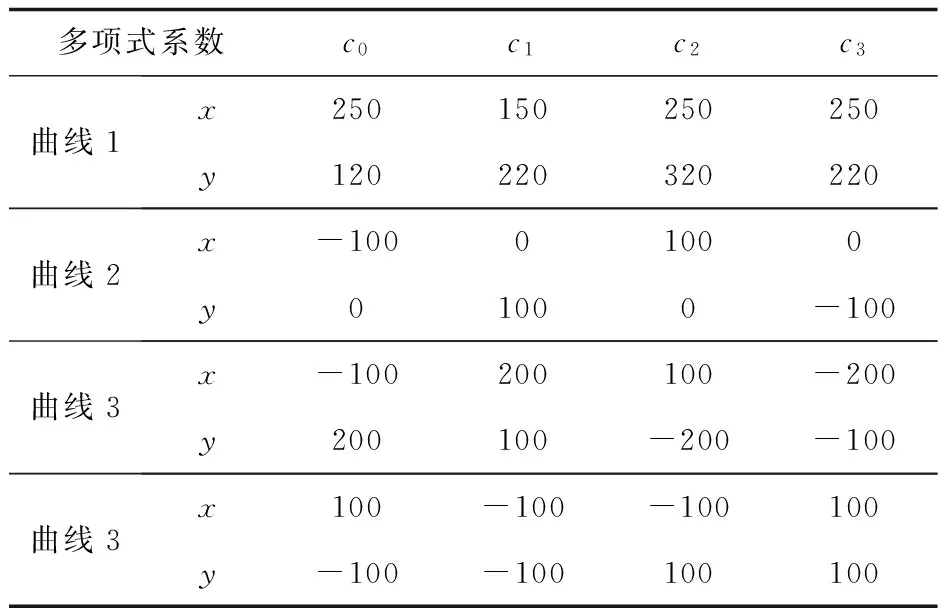
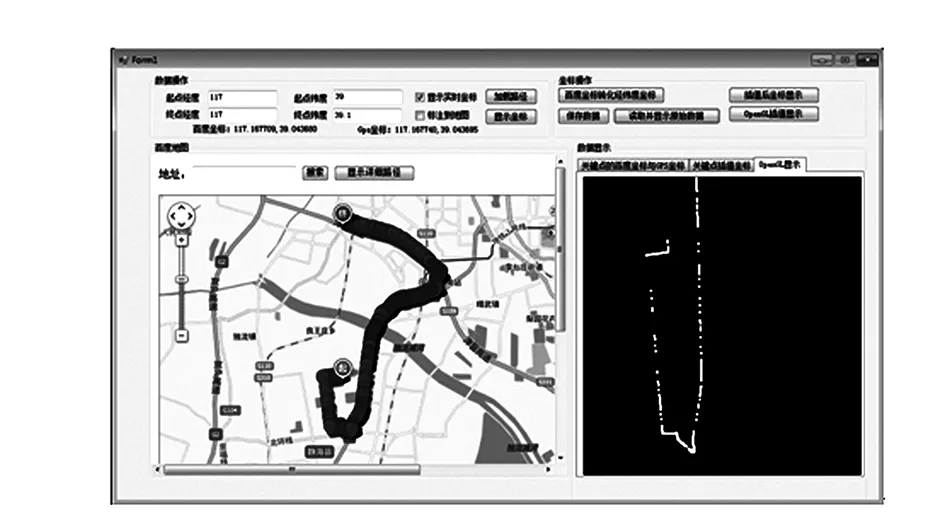
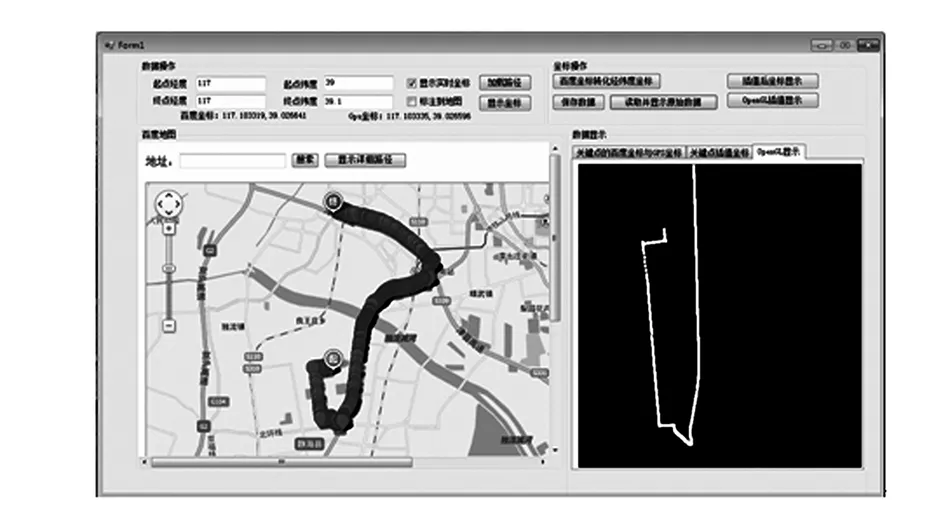
x:a=x0

y:y0y1…yn

三次样条曲线方程满足以下条件：

(1)在每个分段区间[xi,xi+1](i=0,1，…,n-1,x递增)，S(x)=Si(x)都是一个三次多项式；

(2)满足Si(x)=yi(i=0,1，…,n)；

(3)S(x)、导数S′(x)、二阶导数S″(x)在区间[a,b]都是连续的，即S(x)曲线是光滑的。

结合实际情况的样条曲线的端点条件，即自由边界、固定边界、非节点边界等，可以得出三次样条的曲线方程(如图1所示)。从其构造过程可看出给定点是要求横坐标从小到大排列，不能有相同横坐标的点。当插值点的横坐标相差很小而纵坐标相差较大点时插值效果很差。可以看出，三次样条曲线未能达到无人车决策时的要求，应用效果不佳。

图1　三次样条拟合曲线

1.3Catmull-Rom样条曲线的分析

Catmull-Rom样条插值是一种分段函数，它的特征就是每一个点pi处的切线值与它的前后相邻的两个点的斜率成一定的比例，即为t(pi+1-pi-1)。

Catmull-Rom样条为一阶连续，其中t就是张力系数，它影响了拟合曲线在控制点的弯曲程度，Catmull-Rom样条通常将此设定为0.5。

对每两个点pi-1、pi进行分段考虑(如图2所示)，在每一段上，它受4个控制点的影响，分别是pi-2、pi-1、pi、pi+1，既然它是三次的，它就能通过以下多项式函数来表示[11]：

(3)

式中c0、c1、c2、c3为多项式系数。

图2　Catmull-Rom样条曲线原理

为了表示一些参数，本文利用如下初始条件：

(4)

将式(4)代入式(3)中得

(5)

由方程组(5)可解得各个系数值：

(6)

由此可得

(7)

2　Catmull-Rom样条插值算法实验结果

2.1经过给定关键点的比较

为了比较Catmull-Rom样条插值函数结果和样条插值函数计算结果的优劣，在Microsoft Visual Studio 2008开发环境中，首先给出7个关键点，设置在相邻两个点间插值点的数量为5，比较两种方法的结果(如图3—5所示)。

图3　三次均匀B样条插值

图4　三次样条插值

图5　Catmull-Rom样条插值

图3—5中，黑色框中的点表示给出的这7个关键点，叉形点表示利用不同样条插值算法根据这7个点所绘制出来的插值点。

由图3可知，三次均匀B样条形成的曲线较为平滑，而且效率较高，但是不能通过给定的关键点。由图4可知，三次样条曲线尽管能经过给定的控制点，但根据其原理和在编程时发现，其插值需要横坐标从小到大分布，受关键点坐标影响。而由图5可知，Catmull-Rom样条拟合曲线可以较好地解决上述问题，不仅能通过关键点，插值时还不受关键点坐标的影响。

3种插值算法的比较见表1，结合上述的讨论，考虑B样条曲线和三次样条曲线的特点，本文引入了Catmull-Rom样条插值作为曲线插值的方法，不仅能满足经过所有关键点的特点，还能较好地形成闭合曲线，满足实验与工作的需求，取得较好的结果。

表1　3种插值算法比较表

在编程测试中，将这7个点每两个点插入200个点，即插值后生成1 400个点，所需要的时间为11 ms左右。而无人车在运行时大约每100 ms处理几百个道路点，因此Catmull-Rom样条插值在效率上能够支持无人车决策的需要。

2.2Catmull-Rom样条拟合闭合曲线

为了仿真Catmull-Rom样条曲线拟合闭合回路的效果，本文给出了4个关键点，坐标分别为(150,140)、(200,190)、(250,140)、(200,90)。

图6中，黑色方形点表示给定的4个点，叉形点表示根据这4个点，利用Catmull-Rom样条曲线分别在两个点间插入5个点所绘制出来的插值点。通过编程可以看出，此插值点不受点坐标影响，并能经过给定控制点。根据式(3)，各条曲线对应系数见表2。

图6　Catmull-Rom样条插值形成闭合回路实践效果

多项式系数c0c1c2c3曲线1x250150250250y120220320220曲线2x-10001000y01000-100曲线3x-100200100-200y200100-200-100曲线3x100-100-100100y-100-100100100

2.3Catmull-Rom样条拟合与百度地图的结合

为了更好地体现曲线插值的效果与实际用途，利用JavaScript结合百度地图API制作了百度地图的网页，并将其嵌入到C#开发出的程序中(如图7、8左半部分所示)。通过给定起终点，利用百度地图API获取路径规划后的关键点坐标。将百度坐标通过回调函数近似转化为WGS-84坐标。并将这种二维坐标点转化为OpenGL下的三维坐标点，进行显示。在每两个点间插入10个点，插值后坐标显示，并将插值之后的点加入绘制，进行对比，取得较好的效果(如图7、8右半部分所示)。

图7　关键点的OpenGL显示

图8　插值后关键点的OpenGL显示

3　结　语

本文在获得关键点的基础上，将Catmull-Rom样条插值算法应用到无人车路径插值中，并将其与B样条插值算法和三次样条插值算法作对比，从理论和仿真实验上证明了Catmull-Rom样条插值算法的可行性，此算法不仅能弥补B样条插值不能经过关键点的缺点，也能解决三次样条插值受坐标影响的弊端，而且算法效率较高，能够满足无人车决策的需要。

[1]GARGI U, KASTURI R, STRAYER S H. Perfonnance characterization of video-shot-change detection methods[J].IEEE Circuits and System for Video Technology,2000,10(1):1-13.

[2]HAMPAPUR A, JAIN R, WEYMOUTH T.Digital video segmentation[G]//New York,Proceedings of the Second ACM International Conference on Multimedia, 1994:357-364.

[3]王幼民, 徐蔚鸿.机器人连续轨迹控制中的B样条轨迹优化[J].机械设计,2000,10(10):33-34.

[4]王幼民.机器人连续轨迹控制中的Bezier曲线轨迹优化与控制[J].机械传动,2003,3(3):43-47.

[5]SHIMIZU M,KOBUYASHI K,WATANABE K.Clothoidal curve-based path the generation for an autonomous mobile robot[G]//Proc of the 2006 International Joint Conference SICEICASE, 2006:478-481.

[6]张小江,高秀华.三次样条插值在机器人轨迹规划应用中的改进研究[J].机械设计与制造,2008,9(9):170-172.

[7]任重,杨灿军,陈鹰.轨迹规划中的B样条插值算法[J].机电工程,2001,18(5):38-39.

[8]彭辉,曾碧.Hermite三次样条插值的车型机器人路径规划研究[J].计算机工程与应用,2010,46(22):221-224.

[9]陈弘,刘海,乔胜华,等.基于三次样条插值的车辆行驶数据分析[J].汽车技术,2013(8):54-57.

[10] 林夏菲,吴凤鸣. Catmull-Rom插值算法在基于OpenGL的三维地形绘制中的应用实现[J].电脑知识与技术,2008,3(4):788-789,793.

[11]CATMULL E,ROM R.A Class of Local Interpolating Splines:Computer-Aided Geometric Design[M].San Francisco: Academic Press,1974:105.

(编辑：张峰)

Interpolation Algorithm in Key Points of Unmanned Vehicle Navigation Path

LU Feng1, ZHANG Yongjin2, LI Peng3, ZHAO Ming4

(1. Postgraduate Training Brigade, Military Transportation University, Tianjin 300161, China; 2. Military Vehicle Department, Military Transportation University, Tianjin 300161, China; 3. Joint Projection Department, Military Transportation University, Tianjin 300161, China; 4.Unit 96819, Beijing 100088, China)

To solve the problem of interpolation in key points of unmanned vehicle navigation path, the paper studies interpolation algorithm of key points with Catmull-Rom spline interpolation method. After analyzing the algorithm principle of Catmull-Rom spline interpolation, it programs and compares the advantages and disadvantages between B-spline interpolation and cubic spline interpolation method, and puts forward the method of interpolating key points with Catmull-Rom spline interpolation method. The test shows that this interpolation method makes interpolation curve going through key points and the interpolation algorithm will not be affected by coordinate distribution, and the arrangement of point coordinates is not strictly required.

interpolation algorithm; key points of navigation path; unmanned vehicle

2015- 07- 21；

2015- 09- 06．

国家自然科学基金重大项目(91220301).

陆峰(1993—)，男，硕士研究生.

10.16807/j.cnki.12-1372/e.2016.02.021

U412.3

A

1674-2192(2016)02- 0089- 05