基于贝叶斯理论的激光陀螺可靠性评估

唐百胜，江腾飞

（海军驻北京地区导弹配套设备军事代表室，北京100854）

基于贝叶斯理论的激光陀螺可靠性评估

唐百胜，江腾飞

（海军驻北京地区导弹配套设备军事代表室，北京100854）

激光陀螺是一种由多种元器件组成的高可靠性、长寿命的光电器件，在可靠性评估中，可以依据最小薄弱环节定理，基于传统寿命试验，建立激光威布尔分布可靠性模型；但是由于其高可靠性的特点，在可靠性寿命试验中常常得不到失效数据，应用传统的参数评估方法不能对威布尔分布中的未知参数进行估计。贝叶斯原理得到各个时刻的失效概率，进而建立参数的线性回归模型对威布尔模型中的未知参数进行估计，从而得出激光陀螺的可靠性指标，最后对此种方法进行了验证。该方法中贝叶斯估计结合经验信息大大减小了试验样本数，且克服了传统可靠性评估方法依赖失效数据的缺点，在工程应用上具有很高的价值，结果表明了该方法的有效性。

激光陀螺；可靠性；贝叶斯；无失效数据

0　引言

随着现代装备可靠性水平迅速提高，长寿命、高可靠性的产品越来越多，如何得到这类产品的可靠性指标也越来越受人关注。目前对产品可靠性评估有两种方法：古典估计方法和贝叶斯估计方法。古典估计方法主要是以大样本试验为前提，且依赖于失效数据或性能退化数据，不仅时间长，而且破坏性大，成本高。激光陀螺作为一种新型的惯性器件近年来已经成功应用到了航天、航空等领域，主要优点是可靠性高、寿命长等，但是在研制等阶段中可供试验的样本少，无法通过大量可靠性试验来进行可靠性评估，因此，古典估计方法难以对其可靠性进行有效的估计［1-2］。

贝叶斯估计是一种结合先验信息，只需少量的试验数据便可更新得到后验信息，大大减小了试验样本数的估计方法；同时，它可以有效处理无失效数据情况下的可靠性数据分析，更是节约了试验时间和费用。因此，相比于古典估计方法，贝叶斯估计方法更适合用于长寿命、高可靠性产品的可靠性评估。目前，贝叶斯评估方法已在航天、测控等领域有了成功的应用，并取得了一些成果。

1　激光陀螺可靠性模型

1.1激光陀螺的失效模式

本文研究的激光陀螺结构如图1所示。激光陀螺由腔体、抖动机构、阴阳电极、合光棱镜、球面镜、平面镜、压电陶瓷（PZT）、陀螺信号放大与处理电路等部分组成。激光陀螺在工作时，陀螺高压电路给阴阳电极提供高压用以点亮氦氖气体，产生激光。这样逆、顺两方向的激光在腔体内经过镜面的反射进行传输，在合光棱镜处进行合光，形成干涉条纹，干涉条纹是移动的，通过检测每秒的干涉条纹数，经过转换可以计算角速率，经过陀螺信号放大电路的放大与处理可以得到需要的角速率。结构示意图中的抖动机构可以减少陀螺通过锁区的时间，压电陶瓷和平面镜是用于对陀螺的腔长进行控制［3］。

激光陀螺的性能指标有光强、压电陶瓷电压、百秒滑动曲线等，任何一种性能指标出现异常都表示陀螺失效。根据激光陀螺的结构和组成，其元器件可以分为有源器件和无源器件两种，主要失效模式有以下两种：

（1）有源器件的失效模式

激光陀螺的有源器件为抖动机构、电极和陀螺信号放大与处理电路，有源器件的失效模式主要有两种：一个是由于电气原因（静电或供电浪涌等）导致器件损伤或失效；另一个是由于工艺原因引起器件受到机械性损伤乃至折断而失效。

（2）无源器件的失效模式

激光陀螺的光学无源器件为平面镜、合光棱镜、球面镜、腔体、压电陶瓷等。无源器件的失效模式主要有两种：一是由于受机械冲击使压电陶瓷、球面镜、平面镜、合光棱镜碎裂或出现相对于腔体的位移而失效；二是由于震动和冲击，致使腔体破裂导致氦氖气体泄露，影响陀螺点亮或导致激光陀螺功率下降，影响其寿命的失效模式［4］。

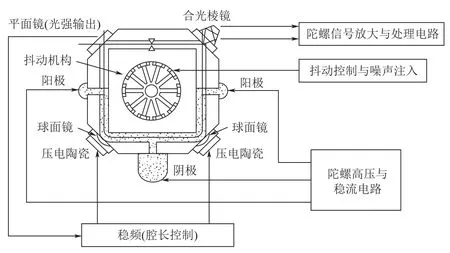
图1　激光陀螺结构示意图Fig.1　Structure diagram of laser gyro

1.2激光陀螺可靠性模型

前面分析了激光陀螺的失效模式，根据激光陀螺的基本结构及各部件的作用，可以认为其可靠性框图为串联结构，如图2所示。

由图2可知，激光陀螺中的可靠性主要受到有源器件的影响。在电工产品的可靠性研究中，大多假设有源器件的失效分布类型为单参数指数分布，也有些研究显示某些电工产品的失效类型分布为威布尔分布，指数分布此时可以看成是威布尔分布的一种特例，并且威布尔分布具有拟合数据能力强的优点，其失效率函数有三种形状（浴盆曲线）即：随时间增加而减少的、常数、随时间增加而增加的，分别对应于浴盆曲线的三个阶段，更符合产品失效的实际［5］。同时，串联的形式可靠性评估中，其失效服从最小薄弱环节定理，因此选择威布尔分布作为激光陀螺的可靠性分布模型。

图2　激光可靠性框图Fig.2　Reliability diagram of laser gyro

2　激光陀螺失效率的贝叶斯估计

2.1激光陀螺失效率先验分布

在威布尔分布下，假设激光陀螺的寿命为t，则有其寿命分布为：

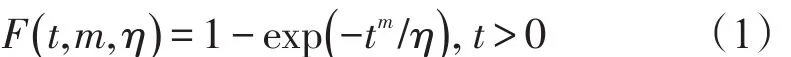
其中，m为形状参数，衡量寿命的离散程度；η为尺度参数，又称特征寿命［6-7］。

由此可得激光陀螺在任意时刻t的失效率为：

激光陀螺在任意时刻t的可靠度为：

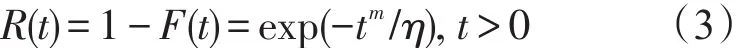
记G（t）=-lnR（t）=tm/η，由函数的凹凸性可得进而可得 R（ti）≥即激光陀螺在任意时刻ti的失效率pi满足：

根据工程实际中对特定时刻tk激光陀螺的失效概率pk的要求给出pk的上界λk，并取［0，λk］上的均匀分布作为pk的先验分布，即：

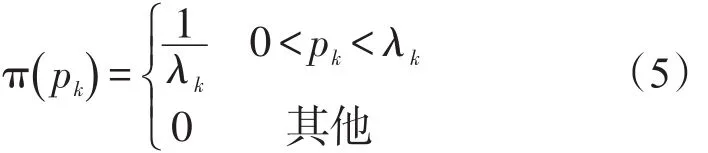
由式（4）可建立激光陀螺在ti时刻的失效概率pi与tk时刻的失效概率pk的保守关系式如下：

因此激光陀螺在ti时刻的失效概率pi的先验分布为：

2.2激光陀螺无失效寿命试验

激光陀螺是高可靠性产品，要想得到其失效数据要耗费很长的时间，成本太高。本文采用常温下的定时截尾寿命试验，得到激光陀螺的无失效数据。

在k次定时截尾寿命试验中，设截尾时刻分别为t1，t2，...，tk（t1＜t2＜...＜tk），相应的试验样品数为n1，n2，...，nk，结果所有样品无一失效，称（ti，ni）i=1，2，...，k为无失效数据。记si=ni+ni+1+...+nk表示到ti时刻，共有si套样品参加试验，且全部没有失效，因此失效数据也可记为（ti，si）i=1，2，...，k。

试验中8套激光陀螺在常温下分别正常工作，在工作到1000h时拿出2套激光陀螺进行检测，2000h时从剩下的激光陀螺中拿出1套进行检测，3000h时又拿出2套，4000h时拿出1套，5000h时对剩下的2套进行检测，结果所有检测激光陀螺都未失效。因此，得到如表1所示的试验数据。

表1　无失效寿命试验数据Table1　Test data of zero failure life

2.3激光陀螺失效率的贝叶斯估计

由试验数据可知，在ti时刻，有si个产品均未出现失效，此时试验数据的似然函数为：

由贝叶斯公式可得激光陀螺失效概率pi的后验分布为：

以期望值作为pi的贝叶斯估计有：

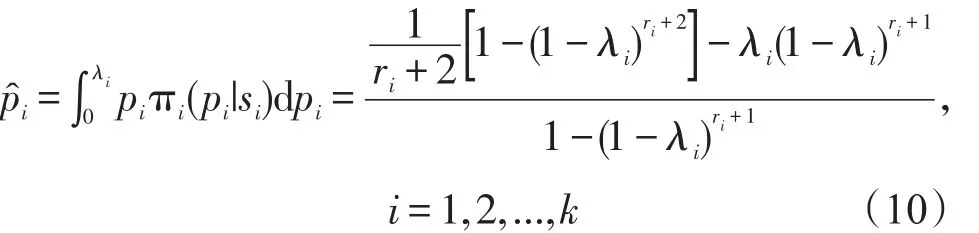
由式（10）以及表1中的试验数据，取λk= 0.01（即5000h的失效率上界），计算得到各时刻失效率pi的贝叶斯估计值，如表2所示。

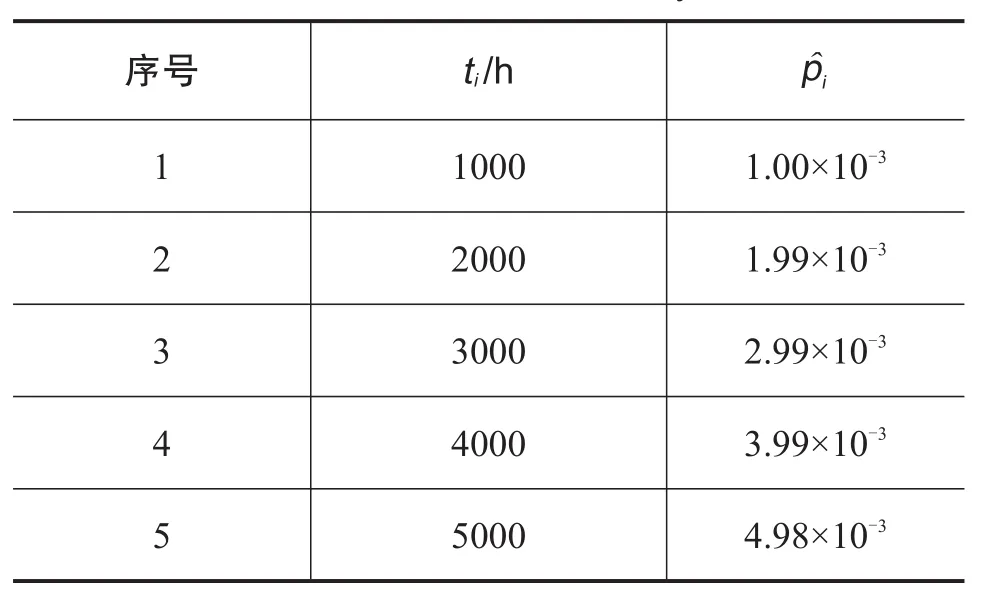
表2　失效率的贝叶斯估计值Table 2　Values of failure rate under Bayesian estimation

3　激光陀螺可靠性估计和仿真

3.1激光陀螺可靠性模型参数估计

在上述得到的各时刻激光陀螺失效率估计值的基础上，利用配分布曲线法拟合出失效率曲线，并用最小二乘法估算出模型参数［8］。

令yi=ln［-ln（1-pi）］，xi=lnti，得：

利用加权最小二乘法进行参数拟合，令：

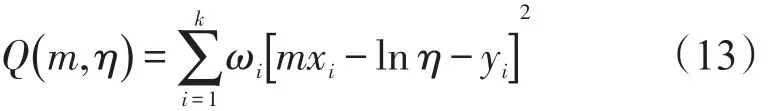
即激光陀螺可靠度的估计为：

3.2激光陀螺可靠性模型仿真与分析

对于上述得到的激光陀螺可靠度函数，采用Matlab仿真了其曲线，如图3所示。

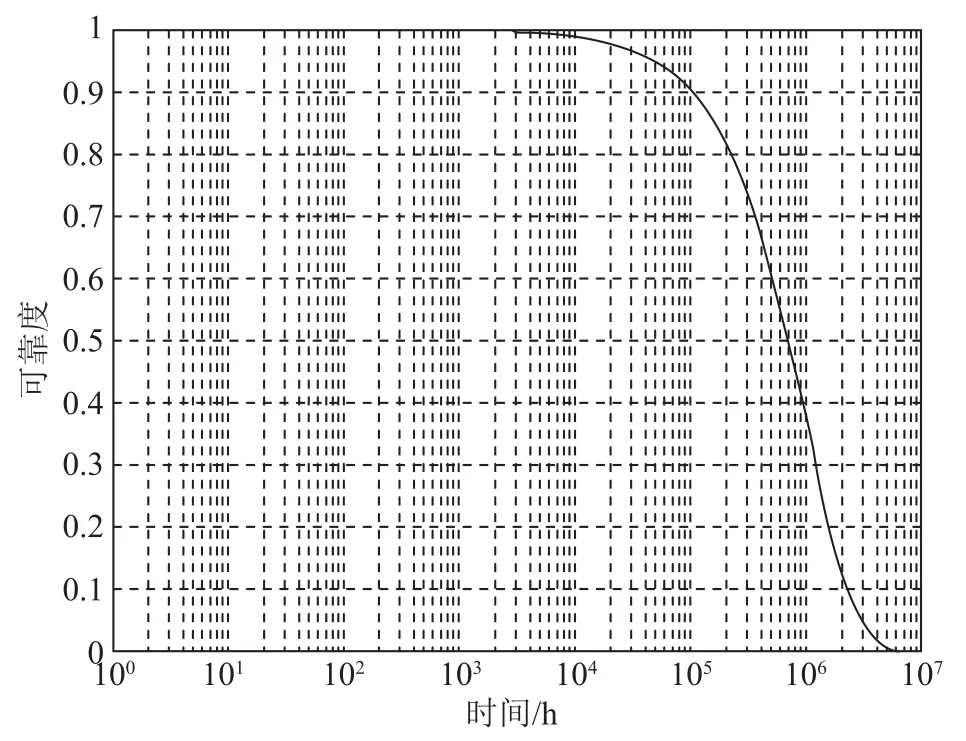
图3　激光陀螺可靠度曲线Fig.3　Reliability curve of laser gyro

从图3可以看出，激光陀螺在开始很长一段时间内可靠度一直为1，在105h时其可靠度为0.9，这也是我们前面的定时截尾寿命试验得到无失效数据的原因。随着时间的增加，其可靠度以指数形式下降，最后再缓慢减小直至为零，即完全失效，可靠度曲线是符合实际的［9-10］。

由估计得到的激光陀螺可靠度函数，我们计算出各时间点激光陀螺的可靠度和失效率如表3所示。

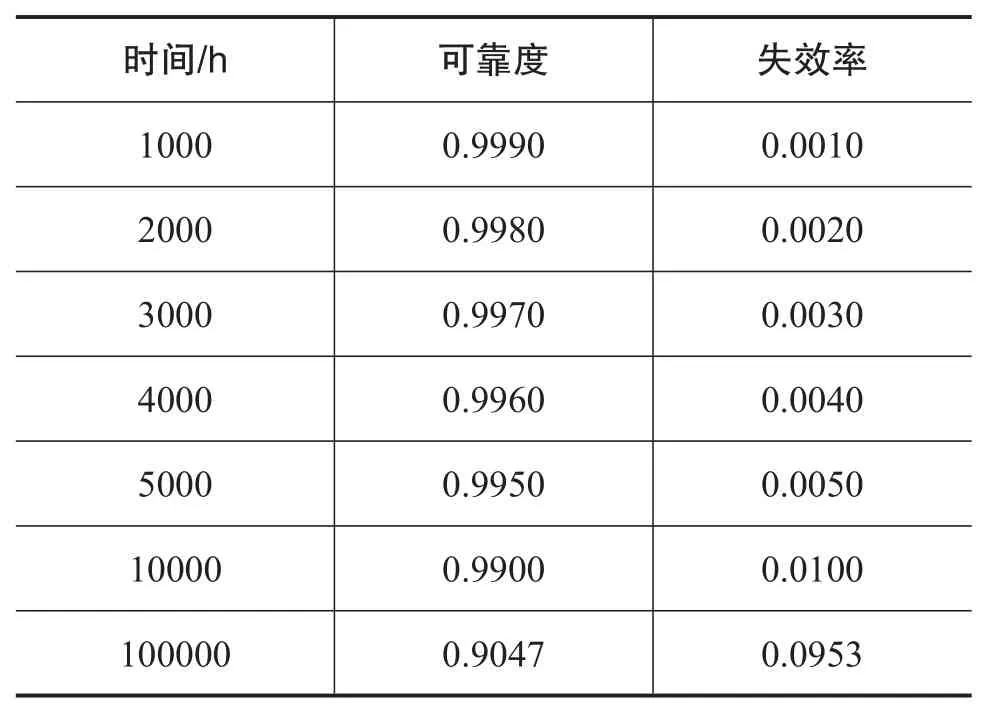
表3　激光陀螺可靠度、失效率估计值Table 3　The estimate of laser gyro reliability and laser gyro failure

显然，此处的结果与表2中由试验数据估计得到的结果相差很小，且激光陀螺在10000h和100000h的可靠度也与实际相符，故此激光陀螺可靠度函数是合理的。

3.3稳健性分析

在本文中，我们根据工程经验，选择了激光陀螺在工作5000h后的最大失效率为λk=0.01，该值的选择完全凭经验，具有一定的主观性，对于同样的产品不同的人选择的λk值会有所不同，而对同一产品，我们需要得到相同的寿命估计，因此，要求计算方法必须具有较好的稳健性，以保证在λk发生扰动时，计算结果不发生较大的改变。为说明λk的选取对统计结果的影响，我们分别取λk=0.01，0.015，0.02，0.025计算激光陀螺的可靠性。计算结果如表4所示。

这样我们得到了不同的λk所对应的四种激光陀螺可靠度函数，为便于观察，我们把这四条可靠度曲线在同一对数坐标中画出，如图4所示。

表4　不同的λk所对应的参数估计值Table 4　The estimate of parameter under differentλk

图4　不同的λk所对应的激光陀螺可靠度曲线Fig.4　Reliability curve of parameter under differentλk

由图4可以看出，不同的λk所对应的激光陀螺可靠度曲线走势一致，说明λk的变化，对参数mˆ和ηˆ的估计，以及激光陀螺可靠性指标的影响不大。由此可见，本方法具有较好的稳健性。

4　结论

本文针对激光陀螺用激光陀螺高可靠性、长寿命的特点提出了无失效数据下基于贝叶斯理论的可靠性评估方法，通过分析激光陀螺失效模式给出了威布尔分布作为其寿命分布，结合先验信息和少量的试验数据估计出了可靠性模型参数，并通过仿真分析说明所得激光陀螺可靠性模型是合理的，且算法具有较好的稳健性。为实际应用中激光陀螺及惯导系统的可靠性评估提供了依据。但处理先验信息相对保守，有待进一步研究得出更精确的可靠性模型。

［1］邓思盛，肖志松，燕路.集成光学陀螺及相关技术研究的现状与展望［J］.物理，2012，41（3）∶179-184. DENG Si-sheng，XIAO Zhi-song，YAN Lu.The status and prospects of integrated optical gyroscopes and related topics［J］.Physics，2012，41（3）∶179-184.

［2］查峰，高敬东，许江宁，胡柏青.光学陀螺捷联惯性系统的发展与展望［J］.激光与光电子学进展，2011，48（7）∶1-4. CHA Feng，GAO Jing-dong，XU Jiang-ning，HU Boqing.Overview on strapdown inertial system consisted by optical gyros［J］.Laser&Optoelectronics Progress，2011，48（7）∶1-4.

［3］秦永元.惯性导航［M］.北京∶科学出版社，2006. QIN Yong-yuan.Inertial navigation［M］.Beijing∶Science Press，2006.

［4］杨海燕.激光陀螺仪失效机理分析与寿命预测方法研究［D］.国防科学技术大学，2005. YANG Hai-yan.Failure mechanism analyzing and lifetime predict method studying on laser gyroscope［D］.National University of Defense Technology，2005.

［5］ Vauchot F，Henn F，Ciuntini J C.A fault tree analysis strategy using binary decision diagrams［J］.Reliability Engineering and System Safety，2002，78（1）∶45-56.

［6］张勇波，傅惠民，王治华.Weibull分布定时无失效数据寿命分散系数［J］.航空动力学报，2012，27（4）∶80-85. ZHANG Yong-bo，FU Hui-min，WANG Zhi-hua.Fatigue life scatter factor analysis for time truncated zero-failure data based on Weibull distribution［J］.Journal of Aerospace Power，2012，27（4）∶80-85.

［7］田霆，刘次华.定数截尾缺失数据下Weibull分布的形状参数近似估计［J］.华侨大学学报（自然科学版），2012，33（2）∶118-120. TIAN Ting，LIU Ci-hua.Approximation of shape parameters for Weibull distribution under censored missing data ［J］.Journal of Huaqiao University（Natural Science），2012，33（2）∶118-120.

［8］刘海涛，张志华.威布尔分布无失效数据的Bayes可靠性分析［J］.系统工程理论与实践，2008，28（11）∶103-108. LIU Hai-tao，ZHANG Zhi-hua.Bayesian reliability analysis of Weibull zero failure data［J］.Systems Engineeringtheory&Practice，2008，28（11）∶103-108.

［9］ Márquez，Fausto Pedro García.Binary decision diagrams applied to fault tree analysis［C］.2008，4thIET International Conference on Railway Condition Monitoring，2008，216（8）∶126-128.

［10］Majdara A，Wakabayashi T J.Proceedings of the institution of mechanical engineers［C］.Proceedings of the Institution of Mechanical Engineers，2010，22（4）∶207-216.

ReliabilityAssessment of Laser Gyroscope Based on Bayesian Theory

TANG Bai-sheng，JIANG Teng-fei
（The Navy Military Representative Office of Missile Equipment in Beijing，Beijing 100854）

The laser gyroscope is a kind of high reliability，long life photovoltaic device which is composed of a variety of components.In the reliability evaluation，the Weibull distribution model is established as the reliability model of the erbium-doped fiber laser in accordance with the smallest weak link theorem，which is based on the traditional life test.However，due to its characteristics of high reliability，the failure data is usually not gotten from the reliability life test.So the traditional parameter estimation method can’t estimate the unknown parameters of the Weibull distribution. The principle of Bayesian is applied to get the probability of failure of each moment，and then is used to estimate the unknown parameters in the Weibull model by establishing the parameters of the linear regression model，to arrive at the reliability index of laser gyroscope.Finally，this method is verified.The method greatly decreases the number of test samples because of Bayesian estimation has taken advantage of experience information，and it overcomes the shortcoming of relying on failure data when using traditional reliability assessment methods.So it has great value on project application.

laser gyroscope；reliability；Bayesian；zero failure data

V241.5+58

A

1674-5558（2016）02-01106

10.3969/j.issn.1674-5558.2016.02.010

2015-04-17

唐百胜，男，硕士，工程师，研究方向为导航、制导与控制。