抗差估计在自由落体式绝对重力仪中的应用

胡　明　张为民　杨　萌　田　蔚　钟　敏

1　中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室，武汉市徐东大街340号，430077



抗差估计在自由落体式绝对重力仪中的应用

胡明1张为民1杨萌1田蔚1钟敏1

1中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室，武汉市徐东大街340号，430077

针对自由落体式绝对重力仪中的异常数据，提出抗差参数估计的数据处理方法。对比分析传统最小二乘拟合与抗差最小二乘拟合计算的重力值，结果表明,抗差参数估计通过合理调整权重因子抑制了异常数据的影响，提高了重力测量精度。

传统最小二乘估计；抗差参数估计；绝对重力仪；自由落体

FG5是目前广泛使用的绝对重力仪产品，结合g9软件，其获得的重力测量精度达μGal级。文献[1]给出了FG5重力仪g9软件数据处理与参数拟合的一般流程；文献[2]从时域上对自由落体各数据权重进行了详细分析与讨论；文献[3-6]在参数拟合公式中增加正弦项与余弦项，抑制激光器调制频率对输出的影响；文献[7]将Lp范数理论应用于绝对重力仪数据处理中，并详细讨论了各种噪声模型的影响。自由落体式绝对重力仪中的时间-距离测量数据难免存在观测粗差，一般采取的舍弃部分初始和结束段数据的预处理方法很难剔除落体数据中的全部粗差。传统最小二乘参数拟合方法适用于近似服从正态分布的测量数据，参数拟合结果对非正态分布的观测粗差极为敏感[7-8]。因此，如何抑制绝对重力仪中异常数据的影响，提高重力仪测量精度，是一个值得深入研究的问题。

本文针对自由落体式绝对重力仪，将抗差参数估计应用到等距离间隔的数据处理中，并与传统最小二乘拟合结果和g9软件处理结果进行对比。结果表明，抗差参数估计采用变权重的方法抑制了异常数据对重力加速度测量的影响；同等条件下，抗差参数估计得到的重力值相对传统最小二乘拟合更接近g9软件的处理结果，提高了重力值测量精度。

1　传统最小二乘拟合

对于自由落体式的高精度绝对重力仪，若忽略重力梯度效应并考虑激光器的波长调制效应，位移测量值xi与时间ti之间的关系可表示为[4-5]：

(1)

式中，x0、v0、g分别为初始位移、初始速度、当地重力加速度，M为干涉条纹分频数，λ为激光波长，ωd为激光器波长调制频率，B和C为正弦项和余弦项相关系数。

根据传统最小二乘拟合标准进行参数估计：

(2)

式中，

(3)

自由落体式FG5重力仪以等距离间隔模式工作，落体棱镜经过相同位移触发相应时刻信号，且随落体棱镜下落速度的增加，时刻数据越来越密集，时间间隔越来越短。若设置重力仪分频数为4 000(即4 000个条纹产生一个时间测量脉冲信号)，单次落体约采集180个时刻点，典型的时刻与时间间隔曲线如图1所示。图1(a)为时刻测量曲线，时刻随点数增加而逐渐增大；图1(b)为4 000分频距离对应的时间间隔，由于落体棱镜下落速度越来越快，时间间隔会随之逐渐变小。在120数据段之后的时间间隔异常跳跃，可能是自由落体系统震动或时间计数器跳跃等所致，在数据处理时需要预先剔除。对多次自由落体数据进行统计分析，大部分数据在120点后产生异常跳跃，所以暂选1～100数据段进行参数拟合。

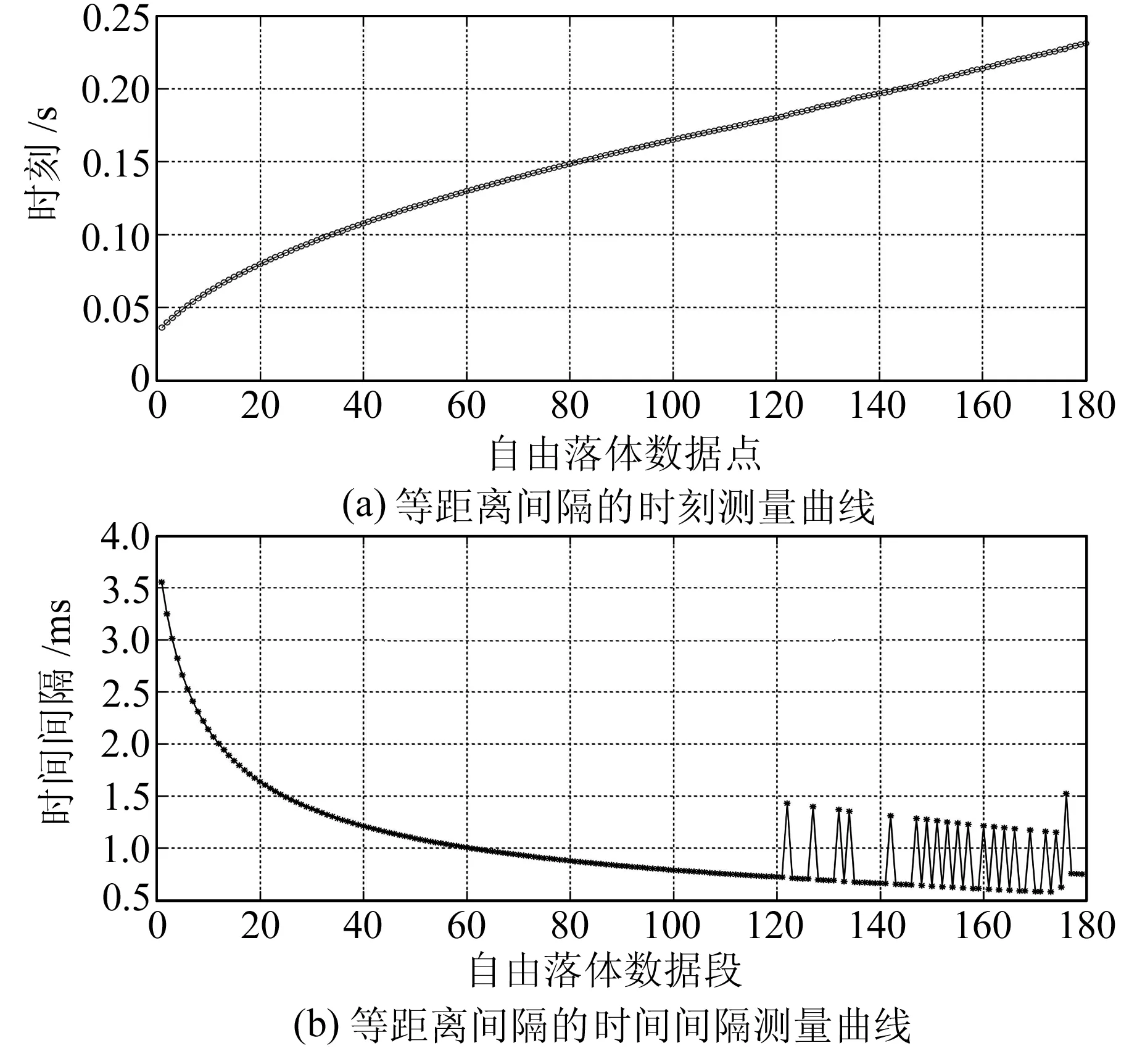
图1　等距离间隔模式下时间测量曲线Fig.1　Time curve for equally spaced in time

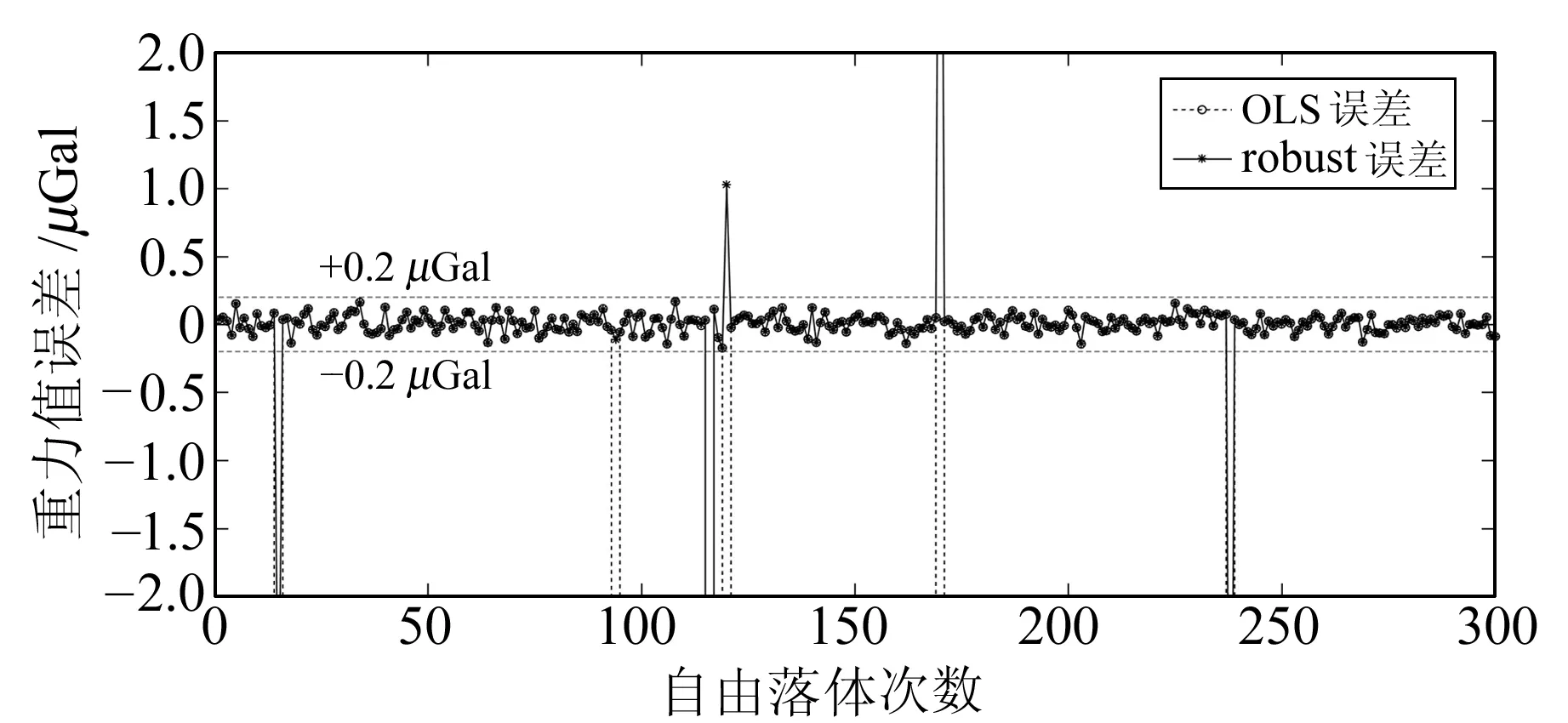
图2　传统最小二乘与抗差最小二乘的重力误差对比Fig.2　Gravity error comparison between ordinary least square and robust trend estimation

在相同参数设置下，将传统最小二乘拟合(OLS)得到的重力值与FG5软件处理结果进行对比。图2中虚线为传统最小二乘拟合与FG5软件计算结果的差异。在300次自由落体数据中，大部分传统最小二乘拟合计算结果与FG5软件计算结果的差异小于0.2μGal，仅有6次自由落体显示巨大差异。对差异较大的6次落体时间序列进行详细分析(图3)，可以看出，在1～100拟合数据中出现异常跳跃，这些异常跳跃直接导致最小二乘拟合的重力值与FG5软件计算结果产生巨大偏离。

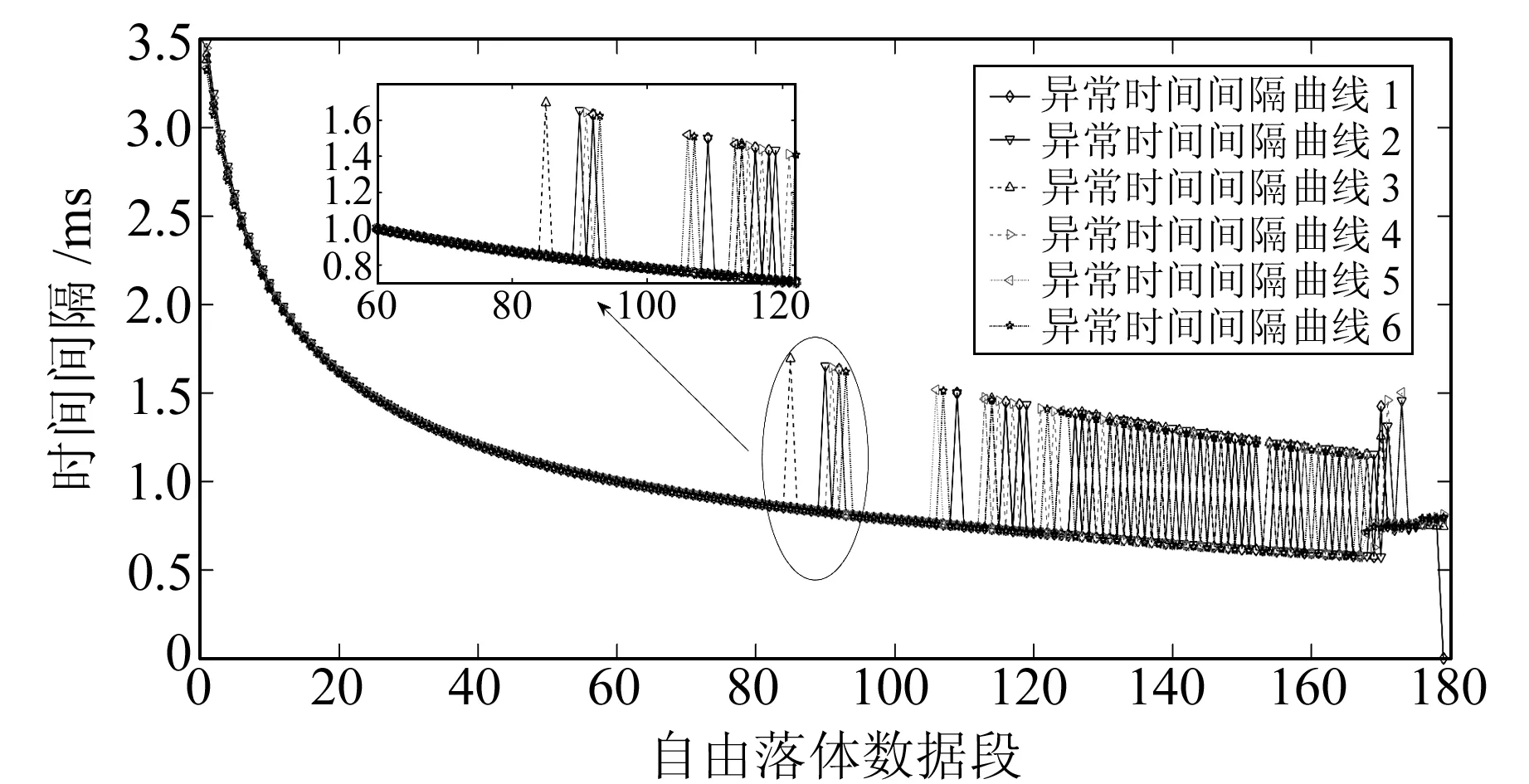
图3　6次差异较大的落体时间间隔曲线Fig.3　Time duration curves of 6 abnormal drops

2　抗差最小二乘拟合

抗差参数估计通过合理设置各数据权重来抑制异常跳跃对重力值的影响：对正常观测值采取保权处理；对非正常但可利用的观测值采取降权处理；对粗差，使其权重为0，在参数拟合中不使用[9-10]。抗差参数估计主要基于迭代的方法来设置各数据点的权重因子，且带加权估计参数矩阵的计算公式可表示为[8]：

图5　传统最小二乘拟合与抗差最小二乘拟合曲线对比(a)和抗差最小二乘中各测量数据的权重(b)Fig.5　Curve fitting comparison between ordinary least square and robust trend estimation(a) and weights of the data for robust trend estimation(b)

采用抗差最小二乘处理自由落体重力仪数据，并与传统最小二乘拟合曲线进行对比(图5(a))。图5(b)给出了抗差估计中各数据点在参数估计中的权重曲线。该权重曲线显示，自由落体测量数据中最后部分数据的权重几乎为0，为异常数据，与图5(a)中曲线相符。对比传统最小二乘与抗差最小二乘的残差位移直方图(图6)显示，采用抗差参数估计使残差位移由10-4m量级减小到约10-9m量级，相对传统最小二乘而言，抗差参数估计的残差位移更接近正态分布。

图6　传统最小二乘拟合与抗差最小二乘拟合的残差位移直方图Fig.6　Distance residuals histogram for both ordinary least square and robust trend estimation

若进行参数拟合的数据段中没有异常点，传统最小二乘法(OLS)和抗差最小二乘法(Robust)与g9软件处理结果的差异都在0.2μGal以内。若进行参数拟合的数据段含有异常跳跃，利用传统最小二乘法与抗差最小二乘法以及g9软件的数据处理结果见表1。表1显示，用传统最小二乘法处理数据得到的重力值与g9软件计算结果差异巨大；采用抗差最小二乘法时，大部分异常数据对重力加速度拟合参数的影响得到抑制，重力值的精度提高约6～8个量级。

表1　传统最小二乘法(OLS)、抗差最小二乘法分别与g9软件处理结果的对比

3　结　语

抗差参数估计应用到自由落体式绝对重力仪的数据处理中，极大地抑制了异常点对重力加速度计算结果的影响，提高了重力值的精度。相对传统最小二乘法而言，抗差参数估计的计算结果与g9软件处理结果差异更小，且能容忍部分异常数据，鲁棒性能良好。同时，该方法也给出了一种鉴别自由落体中异常数据的途径。

[1]Micro-g LaCoste. G9 User’s Manual[Z]. 2012

[2]Nagornyi V D. A New Approach to Absolute Gravimeter Analysis[J]. Metrologia, 1995, 32(3): 201-208

[3]Niebauer T M, Sasagawa G S, Faller J E, et al. A New Generation of Absolute Gravimeters[J]. Metrologia, 1995, 32(3): 159-180

[4]Orlob M. Spectral Analysis of Synthetically Affected FG5 Absolute Gravimeter Residuals[D]. Dallas:University of Texas, 2011

[5]Orlob M. Absolute Gravimetry Instrumentation of FG5 and an Overview of Applications[R]. ENGO 615-Advanced Physical Geodesy Project Report, 2008

[6]Orlob M, Braun A. Impact Estimation and Filtering of Disturbances in FG5 Absolute Gravimeter Observations[J]. International Journal of Geosciences, 2013, 4(2), 302-308

[7]Nagornyi V D, Svitlov S, Araya A. Improving Absolute Gravity Estimates by theLp-Norm Approximation of the Ballistic Trajectory[EB/OL].http://arxiv.org/abs/1509.00750,2015[8]费业泰. 误差理论与数据处理[M]. 北京：机械工业出版社，2000 (Fei Yetai. Error Theory and Data Processing.[M]. Beijing: China Machine Press, 2000)

[9]Holland P W, Welsch R E. Robust Regression Using Iteratively Reweighted Least-Squares[J]. Communications in Statistics-Theory and Methods, 1977, 6(9): 813-827

[10] 杨元喜. 抗差估计理论及其应用[M]. 北京：八一出版社，1993 (Yang Yuanxi. Robust Estimation Theory and Its Application.[M]. Beijing: Bayi Press, 1993)

Foundation support:National Key Scientific Instrument and Equipment Development Project, No.ZDYZ2012-1-04; National Natural Science Foundation of China, No.41504140.

About the first author:HU Ming, PhD, assistant researcher, majors in inertial sensor and gravimeter, E-mail: huming@whigg.ac.cn.

Robust Trend Estimation and Its Application in the Free Fall Absolute Gravimeter

HUMing1ZHANGWeimin1YANGMeng1TIANWei1ZHONGMin1

1State Key Laboratory of Geodesy and Earth’s Dynamics, Institute of Geodesy and Geophysics,CAS, 340 Xudong Street, Wuhan 430077, China

Robust trend estimation is employed for some outliers in the free fall absolute gravimeter. We compare gravity as obtained by ordinary least square estimation and by robust trend estimation. The results show that we can reject outliers by adjusting the weighting factors of the time-distance pairs, thus improving measurement accuracy.

ordinary least square estimation; robust trend estimation; absolute gravimeter; free fall

2015-11-13

胡明，博士，助理研究员，主要从事惯性传感器与重力仪相关研究，E-mail：huming@whigg.ac.cn。

10.14075/j.jgg.2016.09.018

1671-5942(2016)09-0833-04

P223

A

项目来源：国家重大科研装备研制项目(ZDYZ2012-1-04)；国家自然科学基金(41504140)。