断层向错引起的地表重力变化研究
2016-09-21段虎荣崔进业
段虎荣 崔进业 杨 凡
1 西安科技大学测绘科学与技术学院,西安市雁塔路58号,710054
断层向错引起的地表重力变化研究
段虎荣1崔进业1杨凡1
1西安科技大学测绘科学与技术学院,西安市雁塔路58号,710054
利用三维角点法以及空间物体旋转的几何变换理论,建立断层向错与地表重力变化的关系,并进行数值模拟计算。选取断层下盘左端点为旋转基点,分析断层埋深和倾角对其向错引起的重力变化的影响。结果表明,断层向错引起的重力变化与断层埋深有明显的相关性,在W1、W2、W3向错模式下,重力变化均表现为随断层深度增加而逐渐衰减;重力变化对断层倾角有着不同的响应。断层运动产生的重力变化空间分布特征与断层的向错模式以及旋转基点的选择有关。
向错; 重力变化;断层倾角; 三维角点法
学者们利用位错理论能够很好地解释许多地面平移现象[1-3]。断层向错理论可以进一步补充和完善位错理论[4-6]。利用重力资料识别断裂构造已有许多成功的事例,如基于铅垂台阶或倾斜台阶的组合或者利用3D Delaunay剖分算法的重力建模[7]。作者曾经采用两个直立长方体组合模型来模拟逼近铅垂断层向错引起的地面重力变化[8],但现实断层倾角并非是一个定值。本文针对不同倾角、不同埋深的断层向错运动引起的地面点重力变化进行研究,为大地测量学、地球动力学等研究提供理论参考。
1 断层向错引起的地面重力变化
1.1断层向错
图1为基于三维空间直角坐标系描述断层的空间坐标。为方便描述,假设断层、宽度、深度方向分别平行于3个坐标轴,用两个梯形体来模拟断层的上、下两盘(图1(a))。选取断层下盘左端点为旋转基点,绕平行于Z轴方向(深度方向)的轴转动时,称为断层扭张向错模式(图1(b));绕平行于X轴方向(断层走向方向)的轴转动时,称为断层扭转向错模式(图1(c));绕平行于Y轴方向(断层宽度方向)的轴转动时,称为断层扭翘向错模式(图1(d))。断层向错扭张、扭转、扭翘分量分别用W1、W2、W3表示,则引起的地面重力变化可表示为F=f(W1,W2,W3)。

图1 梯形体模型描述向错示意图Fig.1 The disclination described by trapezoid body model
1.2断层向错与重力变化的关系
图1(a)中,设断层几何参数长度为l,宽度为w,深度为d,走向为α,倾角为δ;断层上盘为一空间六面体,在当前坐标系下其顶点为PL1、PL2、PL3…PL8;断层下盘也为一空间六面体,其顶点为PR1、PR2、PR3…PR8。根据三维角点法,可计算观测点P的重力值gA[9]:
(1)
(2)
因此,断层旋转前后观测点P的重力变化为:
(3)
由于断层上、下盘的顶点坐标是关于长度l、宽度w、深度d、走向α、倾角δ等参数的函数,W1、W2、W3分别为断层向错扭张、扭转、扭翘分量,故断层向错引起的重力变化为:
(4)
式中,P(x,y,z) 为计算点的坐标 ,P0(x0,y0,z0)为断层转动基准点坐标,断层转动的轴线由P1(x1,y1,z1)、P2(x2,y2,z2)确定。
1.3断层向错及Okada位错理论模型产生的重力变化
为简化计算和直观描述断层向错,通常引入一簇排列整齐的假想位错,其位于割口平面上并由向错线限定。可以把这种位错簇看作是向错的位错模型。例如,选取断层下盘中点为旋转基点,以过基点并垂直于断层的直线为旋转轴,断层产生扭翘向错(W3)(图2)。根据断层微分的思想,可以将其分解成一簇排列整齐的倾滑位错(U2)子断层。分析断层扭翘向错(W3)运动引起的重力变化,可以分别由作用在假想的位错系统上的倾滑位错(U2)分量引起的形变简单地进行求和计算。

图2 用位错表示向错的模型Fig.2 The disclination simulated with the dislocation
图2为断层产生的扭翘向错(W3)右半部分的侧面示意图, 其中O表示断层底部的中点。距旋转基点的距离越远,倾滑位错(U2)分量的值越大。子断层张倾滑位错(U2)分量值为子断层到旋转基点距离的线性函数,其线性系数为扭翘向错(W3)的正切值。在位错理论中,变形地表的重力变化由空间固定点的重力变化和地表高程变化引起的重力变化两部分组成。本文采用Okada位错理论模型,仅考虑空间固定点的重力变化,且断层错动时产生的空隙不进行填充。在给定相同的断层参数条件下,两种模型的计算结果见图3(黑色线条为断层位置,红色箭头为断层运动的方向,下同)。
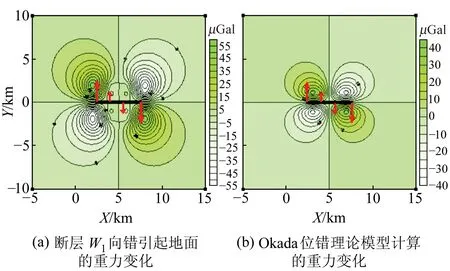
图3 两种模型计算的断层错动重力变化Fig.3 The gravity changes calculated by two models
从图3可以看出,断层在张裂运动模式下,两种模型计算的重力变化分布特征一致、形态相似,数值最大差异为15 μGal。
2 断层向错引起的地表重力变化计算及分析
2.1断层埋深和倾角对向错引起重力变化的影响
为直观理解和认识断层的埋深和倾角对断层向错引起的重力变化的影响,通过式(4)分别计算断层埋深-地表重力变化和断层倾角-地表重力变化。依据图1描述模型,选取断层下盘左端点为旋转基点,断层向错扭张、扭转、扭翘取值为W1=20″、W2=20″、W3=20″,分别计算简单断层在地面某一点的地表重力变化。
由图4可以看出,断层埋深对不同模式的断层向错产生的重力变化响应总体趋势一致,对W3模式的影响最大,对W1模式的影响次之,对W2模式的影响最小。从断层埋深-地表重力变化曲线可以看出,断层向错引起的地表重力变化与断层深度有明显的相关性,3种运动模式均表现为随断层深度增加而地表重力变化逐渐衰减。根据观测到的地面重力变化现象,能够解释浅部断层转动机制;断层较深时,观测到的结果较小,甚至没有变化,埋深超过200 km时断层向错引起的地表重力变化趋于0。
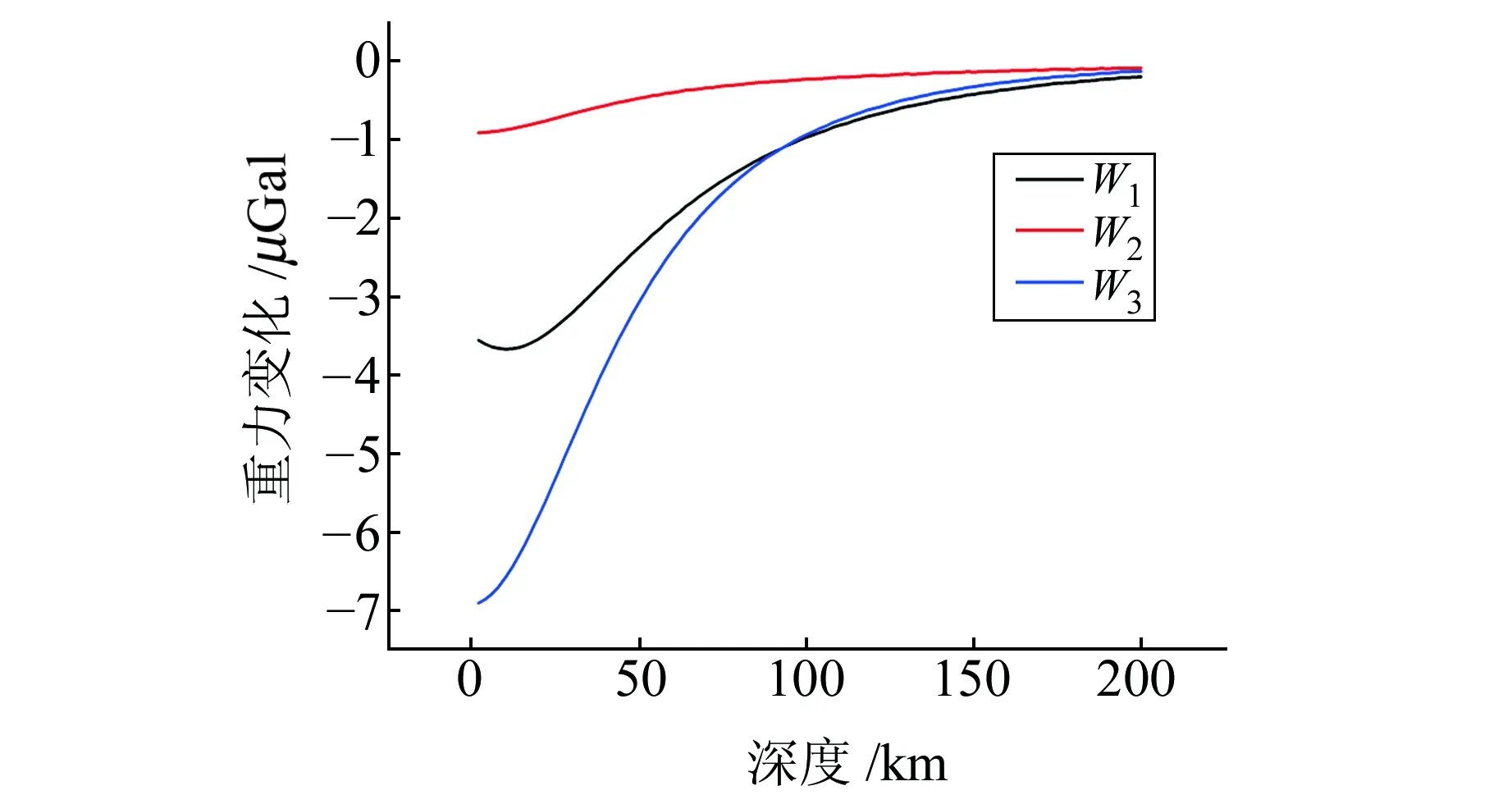
图4 断层埋深-地表重力变化曲线Fig.4 The curve of surface gravity changes and fault depth
从图5可以看出,在扭张W1、扭转W2、扭翘W33种向错模式下,断层倾角的变化对重力变化有着不同的响应。其中断层扭张W1模式对倾角的变化最敏感,重力变化随倾角的增加总体呈现出先减小后增大的变化特征。扭转W2、扭翘W3模式具有相似的响应,随倾角的增大而重力变化减小,但其响应特征相对较弱。

图5 断层倾角-地表重力变化曲线Fig.5 The curves of surface gravity changes and fault dip
2.2地表重力变化空间分布特征
图6是单条断层不同向错模式产生的重力变化空间分布,其中转动基点为断层底部左端点,转轴的选取参照§1.1。计算时,断层参数分别取l=5 km,w=5 km,d=1 km,W1=0.1°,W2=0.1°,W3=0.1°,α=90°,δ=90°。图6(a)、图6(b)、图6(c)分别为单一的扭张、扭转、扭翘向错模式。可以看出,断层向错引起的重力变化空间分布特征与断层的向错模式有关,W1、W2模式的重力变化呈现出以断层为对称轴的几何对称分布,W3模式正值区域大致位于Y∈[-10,0],负值区域大致位于Y∈[0,10],呈现出以断层为对称轴的负对称分布。在数值上,正值区域反映了物质处于挤压状态,负值区域反映了物质处于拉张状态。图6(d)、图6(e)、图6(f)为混合模式W12、W13、W123。与单一模式相比,其重力变化幅度有所增大。W12模式产生的重力变化呈现出对称轴的几何对称分布,W13、W123模式产生的重力变化均为非对称分布。W13、W123模式负值的中心区域均位于Y∈[0,2],重力变化空间分布整体呈现W3模式起主导作用。总之,断层以不同的向错模式产生的重力变化数值大小不同,且重力变化显著区域主要集中在断层两侧附近,与地震破裂过程中同震重力变化的近场剧烈性相吻合。
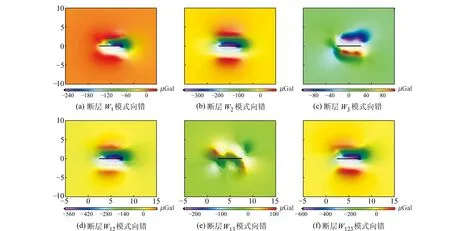
图6 断层向错产生的地表重力变化的空间分布Fig.6 The distribution of gravity changes by fault disclinations
2.3断层向错时转动基点选取对重力变化的影响
断层向错产生的重力变化除了与转动角有关外,还与转动轴和转动基点的选择有关。§2.2中分析了基于断层底部左端点的向错运动,这里仍采用上述断层数据,保持转动轴不变,选取的转动基点分别位于断层底部的l/3、l/2、2l/3、l(右端点)处,来研究基于断层向错扭翘W3模式的重力变化分布情况。
随着基点的选取不同,断层向错产生的重力变化分布也不同(图7)。由图7(a)与图7(c)、图7(d)与图7(c)可以看出,两者均显示重力变化的数值区间一致,图像构成反镜像分布,这是由于其旋转基点是关于断层中点呈镜像分布所致。当旋转基点位于l/2处时,重力变化分布构成四象限中心对称分布。从数值结果来看,当旋转基点位于断层端点时,向错产生的重力变化值最大,位于断层中点时重力变化值最小,位于其他位置时重力变化值介于两者之间。
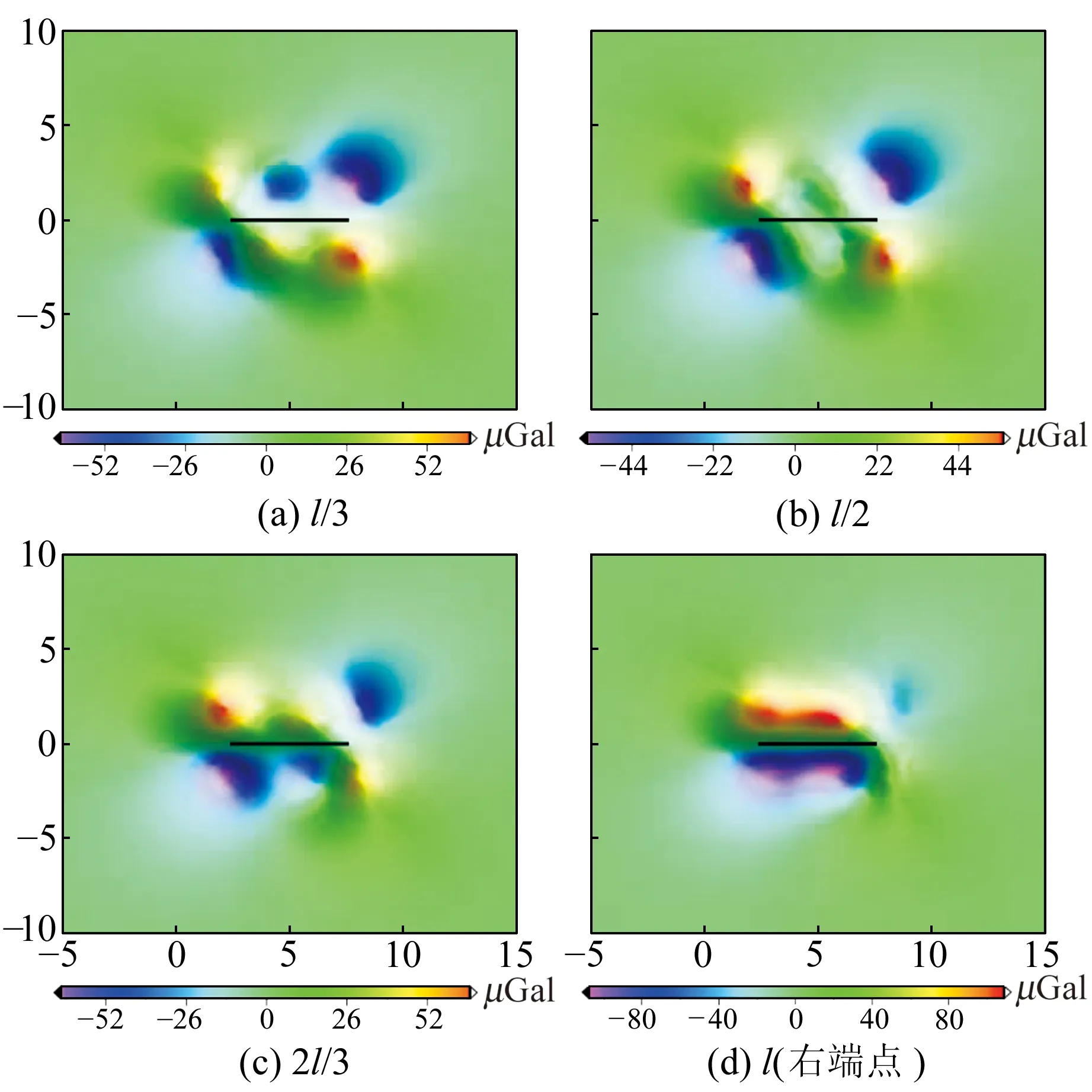
图7 转动基点的选取对重力变化的影响Fig.7 The influences of gravity changes by the rotating basis points
3 讨 论
单纯的位错理论是研究断层在空间的平动现象,而本文的向错理论是研究断层在空间的转动现象。§1.3中利用断层微分思想,将断层的向错现象用断层位错来表示,并与Okada经典模型结果对比,计算结果一方面证明了本文方法的可信度,另一方面也显示了两种模型的差异性。本文方法是在断层向错分量较小,形变后的断层中心位置保持不变的前提下计算的。若断层向错分量过大,这样的表述就不合理。本文只进行了单条断层的简单模拟计算,断层向错产生的重力变化除了与转动角有关外,还与转动轴和转动基点的选择有关,如何确定这两个因素很重要。§2.3中以W3模式分析了旋转基点的选择对重力变化的影响,结果表明,旋转基点位于断层端点时影响最大,而位于断层中点时影响最小。这一结论的前提是旋转基点在上盘与下盘的同一条分割线上,且与断层的向错模式有关。在本文的条件下,若换成W2模式,则结论变为旋转基点对重力变化无影响。基于断层埋深-地表重力变化关系曲线,埋深超过某一深度时地表重力变化趋于0,这一结论与断层本身的参数选取有关,但其趋势不变。此外,本文假设地壳为各向同性均匀介质,而事实上地壳物质并非均匀,也非刚性。
4 结 语
1)断层向错对地表重力变化的影响随断层深度的增加而不断衰减。不同倾角对不同模式的向错引起的地表重力变化有着不同的响应,其中W3模式最为显著。
2)不同向错模式产生的重力变化空间分布特征与断层的向错模式有关。当选取断层底部左端点为旋转基点时,W1、W2单一模式的重力变化均呈现出以断层为对称轴的对称分布,而W3单一模式呈现以断层为对称轴的负对称分布。W12混合模式产生的重力变化呈现出对称轴的几何对称分布,W13、W123混合模式产生的重力变化均为非对称分布,混合向错模式的重力变化幅度大于单一模式。
3)在W3向错模式下,旋转基点位于断层底部端点时对重力变化的影响最大,而位于断层底部中点时影响最小。
[1]孙文科.地震火山活动产生重力变化的理论与观测研究的进展及现状[J].大地测量与地球动力学, 2008, 28(4): 44-53(Sun Wenke. Progress and Current Situation of Research on Theory and Observation of Gravity Change Caused by Seismicity and Volcanism[J]. Journal of Geodesy and Geodynamics, 2008, 28(4): 44-53)
[2]Talebian M, Fielding E J, Funning G J. The 2003 Bam(Iran) Earthquake: Rupture of a Blind Strike-Slip Fault[J].Geophysical Research Letters, 2004, 31(11): 1-4
[3]邵志刚, 武艳强, 江在森, 等. 基于 GPS 观测分析日本9.0 级地震同震位错与近场形变特征[J]. 地球物理学报, 2012, 54(9): 2 243-2 249(Shao Zhigang, Wu Yanqiang, Jiang Zaisen, et al.The Analysis of Coseismic Slip and Near-Field Deformation about Japanese 9.0 Earthquake Based on the GPS Observation[J].Chinese J Geophys ,2011,54(9):2 243-2 249)
[4]张永志,张永,武艳军,等.断层转动与地表变形关系研究[J].大地测量与地球动力学, 2013, 33(2): 8-12(Zhang Yongzhi,Zhang Yong,Wu Yanjun,et al.Relationship between Faults Rotation and Surface Deformation[J].Journal of Geodesy and Geodynamics, 2013, 33(2): 8-12)
[5]曾华霖.重力场与重力勘探[M].北京:地质出版社, 2005(Zeng Hualin.Gravity Field and Gravity Exploration[M]. Beijing:Geological Publishing House, 2005)
[6]Okubo S. Gravity Change Caused by Fault Motion on a Finite Rectangular Plane[J]. Journal of the Geodetic Society of Japan, 1989, 35(2): 159-164
[7]李振海,罗志才,钟波. 基于3D Delaunay剖分算法的重力建模与分析[J]. 地球物理学报, 2012, 55(7): 2 259-2 267(Li Zhenhai,Luo Zhicai,Zhong Bo.Gravity Modeling and Analyzing Based on 3D Delaunay Triangulation Algorithm[J].Chinese J Geophys, 2012, 55(7): 2 259-2 267)
[8]段虎荣,杨凡.铅垂断层向错引起的地表重力变化[J].大地测量与地球动力学, 2015, 35(4): 627-631(Duan Hurong,Yang Fan. A Gravity Changes Theory of Vertical Fault Disclinations[J].Journal of Geodesy and Geodynamics, 2015,35(4): 627-631)
[9]Okabe M. Analytical Expressions for Gravity Anomalies Due to Homogeneous Polyhedral Bodies and Translations into Magnetic Anomalies[J]. Geophysics, 1979, 44(4): 730-741
[10]孙家广.计算机图形学[M].北京:清华大学出版社,1998(Sun Jiaguang. Computer Graphics[M].Beijing:Tsinghua University Press,1998)
Foundation support:National Natural Science Foundation of China,No.41304013, 41374028; Doctoral Foundation of Xi’an University of Science and Technology,No.2014QDJ054.
About the first author:DUAN Hurong,PhD, associate professor,majors in geodesy,E-mail:duanghurong@126.com.
A Gravity Changes Theory of Fault Disclinations
DUANHurong1CUIJinye1YANGFan1
1College of Geomatics,Xi’an University of Science and Technology,58 Yanta Road,Xi’an 710054,China
Using a three-dimensional corner point method and space objects rotating geometric transformations, the relationship between the fault disclination and gravity changes in the earth’s surface is established. The influence of gravity changes on fault depth and dip is discussed by rotating basis points on the left endpoint. The results show that gravity changes are significantly correlated with depth of fault. Gravity changes gradually reduce with the increasing depth of fault in single disclination, orW1,W2andW3modes respectively. Fault dips in different modes have different responses. Surface gravity distribution is related to the disclination mode and rotating basis point.
disclinations;gravity changes;fault dip;three-dimensional corner point method
2016-09-29
段虎荣,博士,副教授,主要研究方向为大地测量,E-mail:duanhurong@126.com。
10.14075/j.jgg.2016.09.003
1671-5942(2016)09-0761-05
P312
A
项目来源:国家自然科学基金(41304013,41374028);西安科技大学博士基金(2014QDJ054)。
