快速路合流区加速车道长度计算方法

李宗平　　李林恒

(西南交通大学交通运输与物流学院,成都610031)



快速路合流区加速车道长度计算方法

李宗平李林恒

(西南交通大学交通运输与物流学院,成都610031)

为了克服现有合流区加速车道长度计算方法的缺点和合理设计快速路合流区,提出了一种新的合流区加速车道长度的计算方法．首先通过分析合流区交通流breakdown现象与加速车道长度的关系,建立了基于车辆占有率的合流区交通流breakdown事件发生概率模型．然后,利用合流区交通流breakdown事件发生的概率,建立了合流区加速车道长度的计算模型．最终实现了根据合流区主路与匝道交通量计算合流区加速车道长度的新方法．该方法不需要假设合流区主路外侧车道交通流车头时距的概率分布,克服了现有方法的不足．以北京市大羊坊的合流区为例,利用该方法绘制了不同主线交通量情况下合流区发生breakdown事件概率随加速车道长度变化的曲线,为合理设计合流区提供了依据．

快速路;合流区;加速车道;交通流breakdown;交通设计

近年来,城市汽车保有量不断增加．为了解决城市交通问题,建设了许多快速道路．快速道路合流区是一般道路交通流驶入快速道路的必经之处,合流区加速车道长度是决定整个快速道路合流区大小的关键．加速车道较短的合流区容易导致交通拥堵和发生交通事故,而加速车道过长的合流区又会造成工程上的资金浪费,因此利用科学有效的方法确定合流区加速车道长度十分重要．

现有的计算合流区加速车道长度的方法一般都是根据间隙接受理论(gap acceptance theory)而提出的．例如李文权等[1]建立了匝道车辆的汇入模型和行驶距离模型,分析了匝道车辆汇入合流区主路的运行状态,最终建立了主路交通量、匝道交通量、匝道车辆临界间隙、主路车头时距及加速车道长度的函数关系;邵长桥等[2]认为主路外侧车道车流的车头时距服从负指数分布,并利用相应的概率统计模型计算加速车道长度．这种加速车道长度计算方法的关键是假设:① 主路外侧车道交通流车头时距服从某一分布;② 主路车辆不避让匝道待汇入车辆;③ 匝道待汇入车辆不强行汇入;④ 匝道待汇入车辆根据其临界间隙接受主路外侧车道的车头间隙而汇入主路．而在实际道路运行中，合流区交通流常常出现主线车辆主动减速避让汇入车辆、汇入车辆强行汇入等有悖间隙接受理论假设的交通行为,可见这类研究的假设存在不足之处．为克服这种不足,Choudhury等[3]对合流区外侧车道主路车辆避让待汇入匝道车辆、待汇入匝道车辆强行汇入、匝道车辆按照间隙接受理论汇入这3种交通行为分别进行了研究,得到的3种情况下的临界间隙计算模型可以弥补间隙接受理论计算方法的缺陷;关羽等[4]也在考虑临界间隙变化的情况下推导出汇入模型,并得到了不同参数的变化对汇入率的影响规律．Kondyli等[5-6]研究了主路车辆主动避让匝道车辆、匝道车辆强行汇入2种汇入方式,利用离散选择理论构建了合流区交通流因这2种汇入方式而发生breakdown现象的概率模型；Elefteriadou等[7]利用交通流发生breakdown现象的概率模型对合流区匝道交通量进行了控制方法研究．

间隙接受理论假设合流区主路外侧车道交通流车头时距服从某一分布,而实际的驾驶行为往往导致合流区主路外侧车道交通流车头时距并不服从同一分布．为克服这一不足,本文利用合流区交通流breakdown概率研究城市快速路合流区加速车道长度的计算方法．该研究对于缓解城市快速路合流区交通拥堵具有一定的指导意义,同时对于合理设计快速路合流区具有一定的参考价值．

1　合流区加速车道长度与breakdown现象

在城市快速路基本路段上交通流比较稳定，而在合流区内匝道车辆的汇入行为,往往会引起合流区交通流紊乱、行车速度降低、交通流密度增大等现象．特别是在合流区加速车道较短、匝道汇入车辆过多时,合流区交通流经常会出现breakdown现象[5-9, 13-16],进而成为城市快速路系统的“瓶颈”地段．

交通流breakdown现象指的是在正常行驶状态下,密集的交通流速度突然急剧减少,同时密度急剧增加的现象．然而,刻画交通流发生breakdown现象的交通流速度的减少程度以及密度增加程度的阈值国际上并没有统一标准,同样反映速度与密度急剧变化的时间阈值国际上也没有统一标准．相关学者认为如果交通流速度下降量超过16 km/h,密度上升量超过5%,持续时间超过10 min,则将这种交通现象定义为交通流breakdown现象[7]．

2　基于breakdown概率的加速车道长度计算方法

城市快速路合流区相对于其服务的交通流而言,如果合流区加速车道长度过短,合流区交通流往往会发生breakdown现象．研究合流区交通流breakdown现象与合流区加速车道长度关系的文献尚不多见,本文将根据文献[16]的研究思路,利用合流区交通流发生breakdown事件的概率模型计算城市快速路合流区加速车道长度．

2.1基于breakdown概率的加速车道长度计算模型

由于人们对于合流区交通流breakdown现象有不同的刻画,因此计算得到了不同的计算交通breakdown事件发生概率的模型(简称BP模型)．Elefteriadou等[7]认为BP模型主要有2类:基于寿命数据统计分析的BP模型和基于离散选择分析的BP模型．

2.1.1基于寿命数据统计分析的BP模型

基于寿命数据统计分析的BP模型如下:

(1)

式中,j为匝道流量阈值, pcu/h;Fj(q)为合流区交通流发生breakdown现象的概率分布函数;qij为观测时间区间i内合流区交通流发生breakdown事件时的主线单车道交通量, pcu/(h·lane);q为实时主线单车道的交通量, pcu/(h·lane);kij为当合流区主线单车道交通量出现q>qij时且所有观测期内匝道流量为j时的观测时间区间数量,这里kij中存在即便q>qij但交通流仍不发生breakdown现象的观测时间区间;dij为所有观察时间区间内匝道流量为j时合流区主线交通量达到qij且一定引起合流区交通流发生breakdown现象的观察时间区间数;B为观测时间区间集合,表示在该集合内所有观测区间的合流区交通流发生breakdown现象；R为合流区匝道交通量为j的观测时间区间集合．

由式(1)可知,通过计算合流区交通流发生breakdown的观测时间区间数量可以计算合流区发生breakdown的概率．

2.1.2基于离散选择分析的BP模型

基于离散选择分析的BP模型如下:

(2)式中,P(B)为合流区交通流发生breakdown事件B的概率;qi为观测时间区间i内合流区交通流发生breakdown的主线交通量(pcu/h);ri为观测时间区间i内合流区交通流发生breakdown时匝道对应交通量(pcu/h);β0,β1和β2为回归系数．

式(2)是基于合流区主路交通量的BP模型．交通流的速度、密度(车道车辆占有率)、流量可以相互转化,由此可见,基于交通量的合流区交通流发生breakdown事件B的概率计算公式(2)可完全改写为基于合流区长度内车道车辆占有率的合流区交通流发生breakdown事件B的概率计算公式．为了计算合流区加速车道长度,将式(2)中观测时间区间i内合流区交通流发生breakdown的主线交通量qi更换为合流区长度内车道车辆占有率di,其计算公式如下:

(3)

式中, l为合流区加速车道长度,m; m1,m2分别为合流区主路与加速车道的车道数量．例如对图1所示的合流区,其m1=3,m2=1．则式(2)可改写为

(4)

由式(4)可知,只要能够探测出合流区交通流发生breakdown现象时的个别观测值P(B),qi,ri, 就能够得到β0,β1和β2等回归系数,进而得到一般意义下的P(B)计算模型．

2.1.3快速路合流区加速车道长度计算模型

如果给定合流区主路服务交通量qi,匝道服务交通量ri,主路与加速车道的车道数m1,m2,在保证合流区交通流发生breakdown概率为P(B0)的情况下(即合流区交通流发生breakdown概率值一定),则根据式(3)、(4)可得到合流区加速车道长度计算模型,即

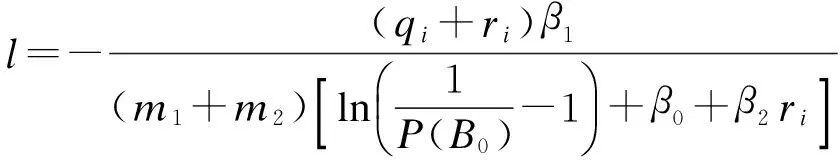
(5)

2.2城市快速路合流区加速车道长度计算方法

通过分析合流区交通流breakdown现象与加速车道长度的关系,对于给定的合流区主路交通量与匝道交通量,本文设计的快速路合流区的加速车道长度计算方法具体步骤如下:

① 根据式(1)计算合流区交通流发生个别breakdown事件B的概率值P(B),及P(B)概率值对应的合流区所有主线单车道交通量qij的总和以及匝道流量j．主线单车道交通量qij的总和与匝道流量j即为式(2)～(4)中的qi和ri．

② 利用P(B),qi,ri的数值、合流区主路与加速车道车道数,以及对应合流区加速车道长度等参数,计算出式(4)的回归系数β0,β1和β2,进而得到一般意义下的P(B)计算模型．

③ 根据主路服务交通量qi、匝道服务交通量ri、合流区主路与加速车道车道数等,在保证合流区交通流发生breakdown概率为P(B0)的情况下,通过式(5)计算特定条件下的合流区加速车道长度值．

由上可知,合流区交通流发生breakdown概率P(B0)值可作为合流区交通拥堵控制指标．该值一般凭实践经验指定,例如文献[7]指定采取控制策略的合流区交通流发生breakdown概率值为0.2．

3　算例分析

3.1合流区发生breakdown现象的经验概率模型

本算例中,数据采集地点为北京市经济开发区大羊坊去北京方向的高速路合流区．大羊坊北京方向合流区的结构为主线单向2车道、匝道1车道与1条加速车道,加速车道长度为250 m．通过观测合流区高峰小时交通流录像,统计得出交通流发生breakdown现象时的数据．采用AutoScope-2004图像处理系统对合流区的高峰小时的交通流录像进行处理后获得交通流量数据．合流区路面传感器装置设置示意图如图1所示．

利用式(1)计算了不同组合的主线与匝道交通量数据下发生breakdown事件的概率,共计15组,结果如表1所示．

根据表1数据,利用回归计算得到式(4)中的3个回归参数,分别为β0=-21.626 329,β1=4.161 569和β2=0.002 774,进而得到一般意义下基于合流区长度车道车辆占有率计算breakdown事件发生概率的BP模型A:

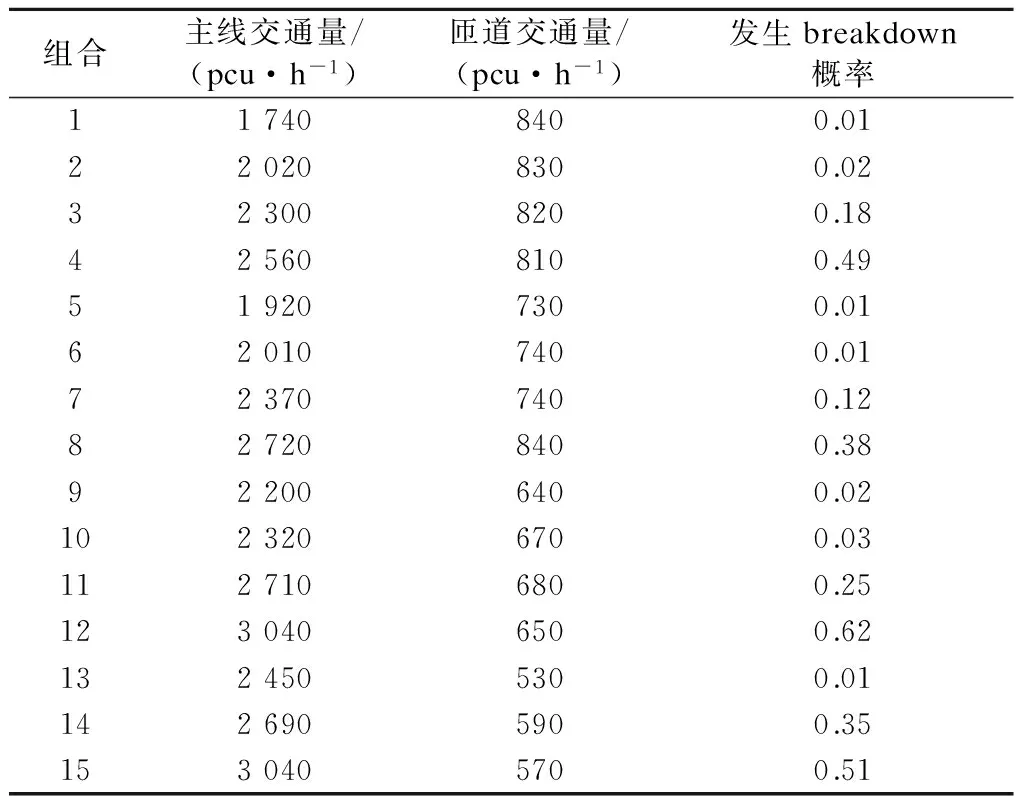
(6)

3.2模型验证

根据表1数据,通过回归计算得到式(2)中的3个回归参数,分别为β0=-21.626 329,β1=0.005 549和β2=0.008 323,进而得到一般意义下基于合流区主路交通量计算breakdown事件发生概率的BP模型B:

(7)

对给定合流区，式(6)与(7)计算结果基本一致，拟合度较好.图2为利用BP模型A与BP模型B对合流区若干组数据进行拟合得到的曲线.由图可见，这2种BP模型的计算结果基本一致.

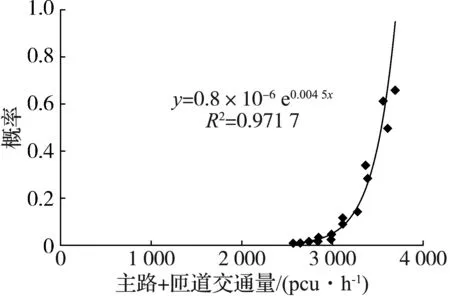
(a) BP模型A

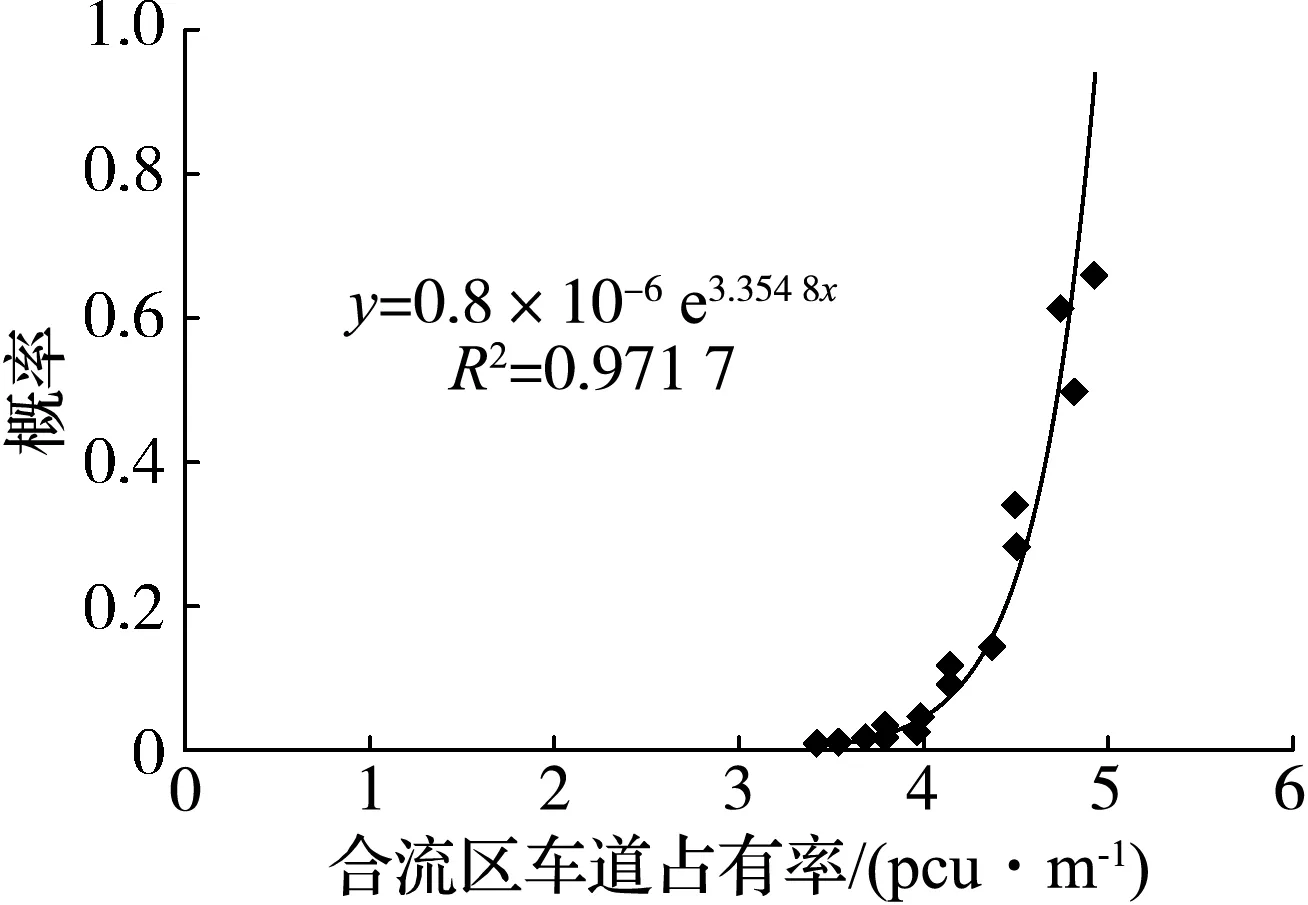
(b) BP模型B

Marczak等[8]于2013年利用直升机分别对荷兰Bodegraven、法国Grenoble的2个合流区进行了实际观测, 发现荷兰 Bodegraven的合流区中,曾经在出现车辆走走停停现象后很快就发生了交通拥堵．他们观测的合流区的具体交通量与主路车道数、加速车道数及加速车道长度等数据见表2．据Marczak等[8]的调查数据,利用本文方法进行计算,并将计算结果与Marczak等[8]的调查结果进行比较验证．

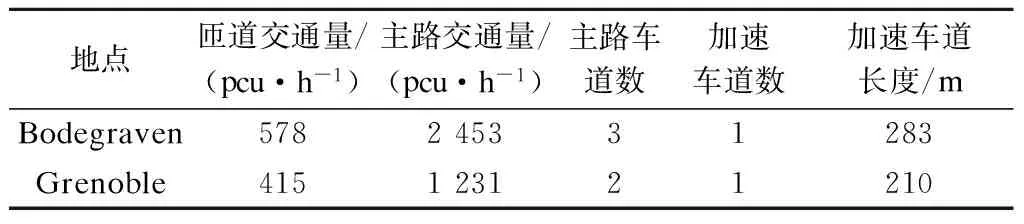
表2　观测的2个合流区的数据[8]

利用模型A可计算出Bodegraven合流区与Grenoble合流区发生breakdown事件的概率分别为0.14与0.07,与观测结果一致．在其他参数不变的情况下,将合流区的加速车道长度分别减少20 m,利用模型A可计算出Bodegraven合流区与Grenoble合流区发生breakdown事件的概率分别为0.32与0.21,可见合流区加速车道长度对于breakdown事件的发生概率影响较大．

3.3计算方法示例

设定主路交通量、匝道交通量组合为表1所示的15种交通状况组合,构造如图1所示的合流区(即主路2车道、加速车道1车道),并利用模型A绘制出合流区交通流发生breakdown现象概率随加速车道长度变化的15条概率分布曲线(图3)．

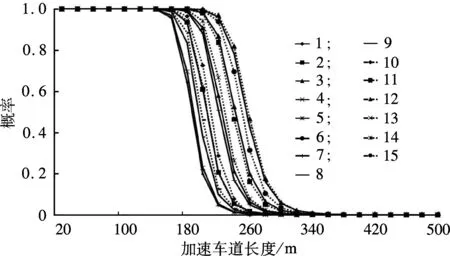
图3　合流区交通量发生breakdown事件的概率分布曲线

在保证发生breakdown事件的概率一定(例如0.1)的情况下,利用合流区发生breakdown事件的概率曲线,可以确定给定主线交通量、匝道交通量的加速车道长度值．例如,对于组合8,主线2车道交通量合计达到2 720 pcu/h,入口匝道交通量为840 pcu/h,如果规定合流区交通流允许发生breakdown的概率为0.1,则由式(5)计算得到加速车道长度应该为255 m．同样,如果规定合流区交通流允许发生breakdown的概率为0.2,则加速车道长度应该为276 m．

4　结语

城市快速路合流区设计的核心是确定加速车道长度.现有加速车道长度计算方法主要依据间隙接受理论,这类算法的核心是假设合流区主路外侧车道的车头时距服从某一分布,但合流区交通流实际运行中常常出现主线车辆主动变换车道或减速避让匝道汇入车辆、匝道汇入车辆强行汇入等交通现象而导致合流区主路外侧车道的车头时距并不服从同一分布．本文利用合流区交通流发生breakdown现象概率计算快速路合流区加速车道长度,该方法避免了间隙接受理论的微观假设条件．实例分析与比较验证表明,获得的算法思路简单、符合实际,具有一定的合理性和可行性．该方法可以为合理设计快速路合流区提供一定的参考依据．

References)

[1]李文权, 王莉, 王炜. 高速公路上匝道合流区通行能力经验模型[J]. 交通运输工程学报, 2004, 4(2):80-84. DOI:10.3321/j.issn:1671-1637.2004.02.019.Li Wenquan, Wang Li, Wang Wei. Empirical highway capacity model of on-ramp junction[J].JournalofTrafficandTransportationEngineering, 2004, 4(2):80-84. DOI:10.3321/j.issn:1671-1637.2004.02.019.(in Chinese)

[2]邵长桥, 荣建. 加速车道长度计算模型及其影响因素[J]. 北京工业大学学报, 2008, 34(1):72-75.

Shao Changqiao, Rong Jian. Research on model of computing acceleration lane length and analysis of its influence factors[J].JournalofBeijingUniversityofTechnology, 2008, 34(1):72-75.(in Chinese)

[3]Choudhury C F, Ben-Akiva M, Toledo T, et al. Modeling cooperative lane changing and forced merging behavior [C/OL]//The86thAnnualMeetingoftheTransportationResearchBoard. Washington, DC, USA, 2007. https://www.researchgate.net/publication/256456929_Modeling_Cooperative_Lane-changing_and_Forced_Merging_Behavior.

[4]关羽, 张宁. 可变临界间隙条件下的加速车道车辆汇入模型[J]. 公路交通科技, 2010, 27(6):117-120,126. DOI:10.3969/j.issn.1002-0268.2010.06.021.

Guan Yu, Zhang Ning. Vehicle merging model for acceleration lane under condition of changeable critical headway[J].JournalofHighwayandTransportationResearchandDevelopment, 2010, 27(6):117-120,126. DOI:10.3969/j.issn.1002-0268.2010.06.021.(in Chinese)

[5]Kondyli A, Elefteriadou L. Modeling driver behavior at freeway-ramp merges [J].TransportationResearchRecord:JournaloftheTransportationResearchBoard, 2011, 2249: 29-37.

[6]Kondyli A, Elefteriadou L, Brilon W, et al. Development and evaluation of methods for constructing breakdown probability models[J].JournalofTransportationEngineering, 2013(9):931-940. DOI:10.1061/(asce)te.1943-5436.0000574.

[7]Elefteriadou L, Kondyli A, Brilon W, et al. Enhancing ramp metering algorithms with the use of probability of breakdown models [J].JournalofTransportationEngineering, 2014, 140(4): 04014003. DOI:10.1061/(ASCE)TE.1943-5436.0000653.

[8]Marczak F, Daamen W, Buisson C. Merging behaviour: Empirical comparison between two sites and new theory development[J].TransportationResearchPartC:EmergingTechnologies, 2013, 36:530-546.DOI:10.1016/j.trc.2013.07.007.

[9]Marczak F, Daamen W, Buisson C. Key variables of merging behaviour: Empirical comparison between two sites and assessment of gap acceptance theory[J].Procedia—SocialandBehavioralSciences, 2013, 80:678-697. DOI:10.1016/j.sbspro.2013.05.036.

[10]Chu T D, Miwa T, Morikawa T. Modeling speed adjustment behavior of merging vehicles at urban expressway merging sections[J].Procedia—SocialandBehavioralSciences, 2014, 138:116-126. DOI:10.1016/j.sbspro.2014.07.187.

[11]Guo Z, Wan H, Zhao Y, et al. Driving simulation study on speed-change lanes of the multi-lane freeway interchange[J].Procedia—SocialandBehavioralSciences, 2013, 96:60-69. DOI:10.1016/j.sbspro.2013.08.010.

[12]Cao W, Mukai M, Kawabe T, et al. Cooperative vehicle path generation during merging using model predictive control with real-time optimization[J].ControlEngineeringPractice, 2015, 34:98-105. DOI:10.1016/j.conengprac.2014.10.005.

[13]Shiomi Y, Yoshii T, Kitamura R. Platoon-based traffic flow model for estimating breakdown probability at single-lane expressway bottlenecks[J].TransportationResearchPartB:Methodological, 2011, 45(9):1314-1330. DOI:10.1016/j.trb.2011.05.008.

[14]Hassan N A, Ibrahim S A H. Analysis of multi-level queueing systems with servers breakdown by using recursive solution technique[J].AppliedMathematicalModelling, 2013, 37(6): 3714-3723. DOI:10.1016/j.apm.2012.07.013.

[15]Kerner B S, Klenov S L, Hermanns G, et al. Effect of driver over-acceleration on traffic breakdown in three-phase cellular automaton traffic flow models[J].PhysicaA:StatisticalMechanicsandItsApplications, 2013, 392(18):4083-4105. DOI: 10.1016/j.physa.2013.04.035.

[16]李林恒, 李宗平, 李远辉. 合流区匝道交通量控制指标计算方法研究[J]. 交通运输工程与信息学报,2015, 13(3):64-69. DOI:10.3969/j.issn.1672-4747.2015.03.011.Li Linheng, Li Zongping, Li Yuanhui. Computational method of control indicators for ramp traffic volume in the merging area[J].JournalofTransportationEngineeringandInformation, 2015, 13(3):64-69. DOI: 10.3969/j.issn.1672-4747.2015.03.011. (in Chinese)

Computational method of acceleration lane length in expressway merging area

Li ZongpingLi Linheng

(School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 610031, China)

In order to overcome the shortcomings of the existing methods for calculating the length of acceleration lane in the merging area and reasonably design the merging area of the expressway, a new method for calculating the length of acceleration lane in the merging area is studied. First, by analyzing the relationship between the breakdown phenomenon and the acceleration lane length, a probability model of traffic flow breakdown event in the merging area based on the vehicle occupancy rate is established. Then, the model for calculating the length of the acceleration lane in the merging area is established by the breakdown probability. Finally, the new method for calculating the length of the acceleration lane in the merging area based on the main road and ramp traffic volumes is proposed. The method does not need to assume that the headway probability distribution of the traffic flow in the outer lane of the main road in the merging area, which can overcome the shortcomings of the existing calculation methods. Taking the merging area of Dayangfang in Beijing City as an example, the curves of the breakdown event probability with the acceleration lane length at different mainline traffic volumes are plotted by the method. The study provides a basis for the reasonable design of the merging area.

expressway; merging area; acceleration lane; traffic flow breakdown; traffic design

10.3969/j.issn.1001-0505.2016.04.036

2015-10-16.作者简介: 李宗平(1963—),男,博士,教授,博士生导师,zpli@swjtu.cn.

国家自然科学基金资助项目(51578465).

10.3969/j.issn.1001-0505.2016.04.036.

U491.1

A

1001-0505(2016)04-0888-05

引用本文: 李宗平,李林恒.快速路合流区加速车道长度计算方法[J].东南大学学报(自然科学版),2016,46(4):888-892.