一种处理交点退化现象的高效多边形裁剪算法
2016-09-21王慧青崇素文
王慧青 崇素文
(1东南大学仪器科学与工程学院, 南京210096)(2展讯通信(上海)有限公司, 上海 201203)
一种处理交点退化现象的高效多边形裁剪算法
王慧青1崇素文2
(1东南大学仪器科学与工程学院, 南京210096)(2展讯通信(上海)有限公司, 上海 201203)
针对复杂多边形裁剪中出现的多边形彼此间重点和重边现象,提出了一种能够处理交点退化现象的高效多边形裁剪算法.该算法利用单向链表实现多边形的存储,同时基于单调链的平面扫描法求解多边形间的交点,减少了多边形顶点的遍历次数和求交次数;对于重点和重边现象,通过交点关联的线段间的方向关系判别交点的进出性;最后更新多边形顶点序列,获取裁剪结果.实验结果表明,该算法能够完成对含内环多边形的裁剪,在交点退化情况下也能获得准确的裁剪结果.且该算法裁剪效率较Greiner-Hormann算法大幅提高,具有很高的执行效率和实用性.
多边形裁剪;交点退化;单向链表;方向关系
多边形裁剪算法被广泛地应用于计算机图形学、地理信息系统(GIS)[1]及相关领域,其目的是提取裁剪多边形与主多边形(被裁剪多边形)的相交区域.常用的裁剪算法有Weiler-Atherton算法[2]、Vatti算法[3]及Greiner-Hormann算法[4],后两者在复杂性和运行效率方面优于前者,但都能实现对一般多边形的裁剪.为了进一步提高裁剪效率及处理复杂多边形裁剪问题,刘勇奎等[5]以Greiner-Hormann算法为基础,优化了交点数据结构和计算方法,提出了两多边形的边重合或者两多边形在顶点处相交的特殊情况的处理思路,但未给出具体实现方法.张钧等[6]通过简化交点和多边形顶点数据结构,减少了多边形间求交次数,能正确裁剪一般多边形,并提高了裁减效率.王结臣等[7]提出了基于梯形分割技术的复杂多边形裁剪方法,该方法裁剪效率较高,但未使用实际复杂多边形验证其可行性.综上,目前多边形裁剪算法在复杂多边形裁剪和重点重边(又称为交点退化现象)等问题上需要进一步研究.
本文基于Greiner-Hormann算法,提出了一种能够处理交点退化现象的多边形裁剪算法.该算法采用单向链表实现多边形存储,利用基于单调链的平面扫描法求解多边形间的交点,对于重点重边问题,基于交点关联的线段间的方向关系来判别交点的进出性,最终依据交点的进出性依次遍历顶点序列,得到裁剪结果.该方法不论是对一般多边形还是复杂多边形均能取得正确的剪裁结果.
1 多边形裁剪算法的一般流程
多边形裁剪算法需要能够完成主多边形与裁剪多边形都为任意多边形时的几何计算,其主要过程如下:
① 将多边形的顶点序列转化为裁剪算法所使用的双向链表数据结构.
② 采用平面扫描法判别出存在相交关系的线段,并求解交点值.
③ 判别交点的进出性.
④ 将交点插入到顶点序列数据结构中,构成新的顶点序列.
⑤ 根据交点的进出性依次遍历顶点序列,得到裁剪结果.
2 基于线段方向关系的交点退化现象处理
2.1交点进出性判别方法
入点和出点是Greiner-Hormann算法中很重要的2个概念.如图1所示,入点和出点定义如下:假设点i为主多边形A和裁剪多边形B的一个交点,如果沿着A的边界方向,可在点i处从B外部进入B内部,则称点i为一个进点;如果沿着A的边界方向,可在点i处从B内部出到B外部,则称点i为一个出点[8].
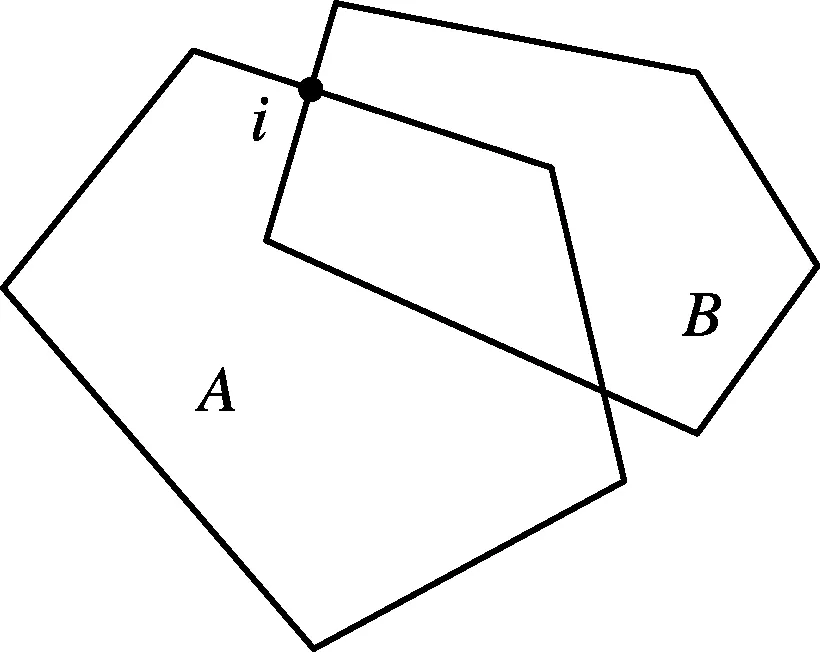
图1 两多边形相交图
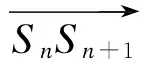
(1)
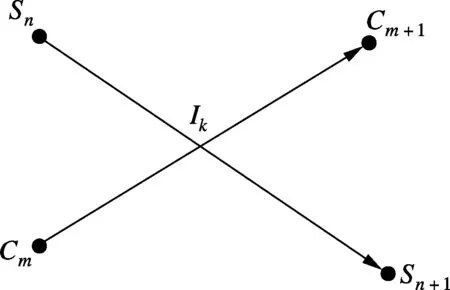
图2 相交矢量线段SnSn+1→和 CmCm+1→
由式(1)得
(2)

2.2交点退化问题分析
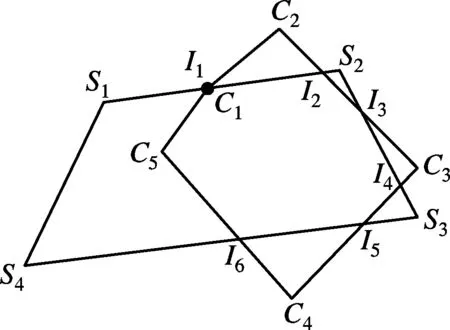
交点的退化现象大致可分为2种情况:① 存在一个交点是某个多边形顶点,即图3中所示多边形重点现象;② 存在2个及以上且连续的交点是多边形顶点,即图4中所示多边形重边现象.主多边形用S={S1,S2,S3,S4}表示,裁剪多边形用C={C1,C2,…,C5}表示,两多边形交点集合用In={I1,I2,…,Ii,…,Ik}表示.
图3(a)中交点I1与顶点C1重合;图3(b)中交点I1与顶点C1重合,且边C1C2和C1C4在边S1S2的内侧;图3(c)中交点I1与顶点S1和C1重合,且边C1C2和C1C5在多边形的外侧.以上3种情况都是由于交点与多边形顶点重合而无法判断交点的进出性,同时也造成了交点的冗余.
(a)
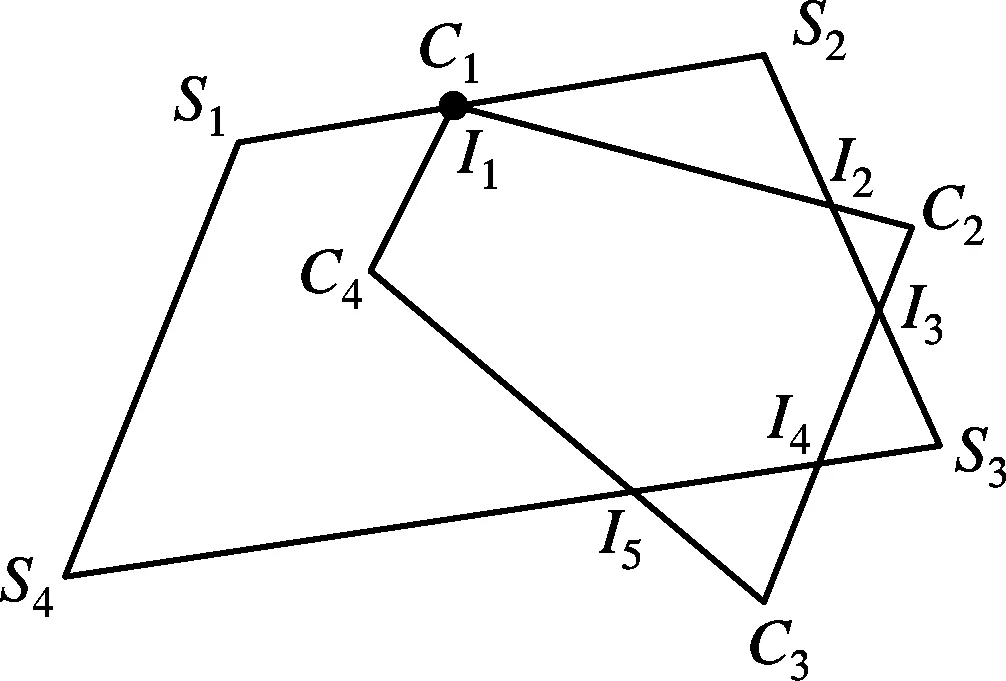
(b)

(c)
图4(a)中交点I1与顶点S1和C1重合,交点I2与顶点C2重合,从而边S1S2与边C1C2的重合部分为I1I2;图4(b)中交点I1与顶点C1重合,交点I2与顶点C2重合,从而边S1S2与边C1C2的重合部分为I1I2;图4(c)中交点I1与顶点C1和S1重合,交点I2与顶点C2和S2重合,交点I6与顶点C5重合.以上3种情况均存在连续交点退化而导致的重边现象.
2.3交点退化问题的解决方法
2.3.1交点的数据结构
交点的数据结构影响多边形裁剪中交点进出性的判别及裁剪结果的构建.本文设计的交点数据结构中主要信息包括:交点的坐标信息Coordinate,产生交点Ik的相交线段的前一个点在主多边形和裁剪多边形顶点的序号SegmentIndex, 交点Ik与该顶点的距离Distance,交点的进出性ioAttri(值为1是进点,值为0是出点,默认值为-1).
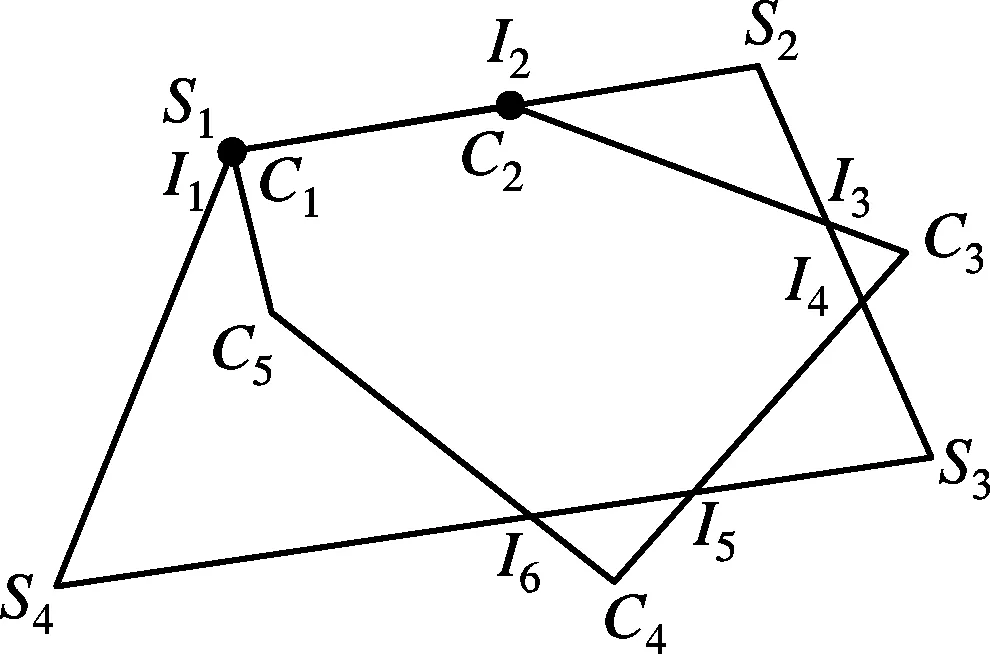
(a)
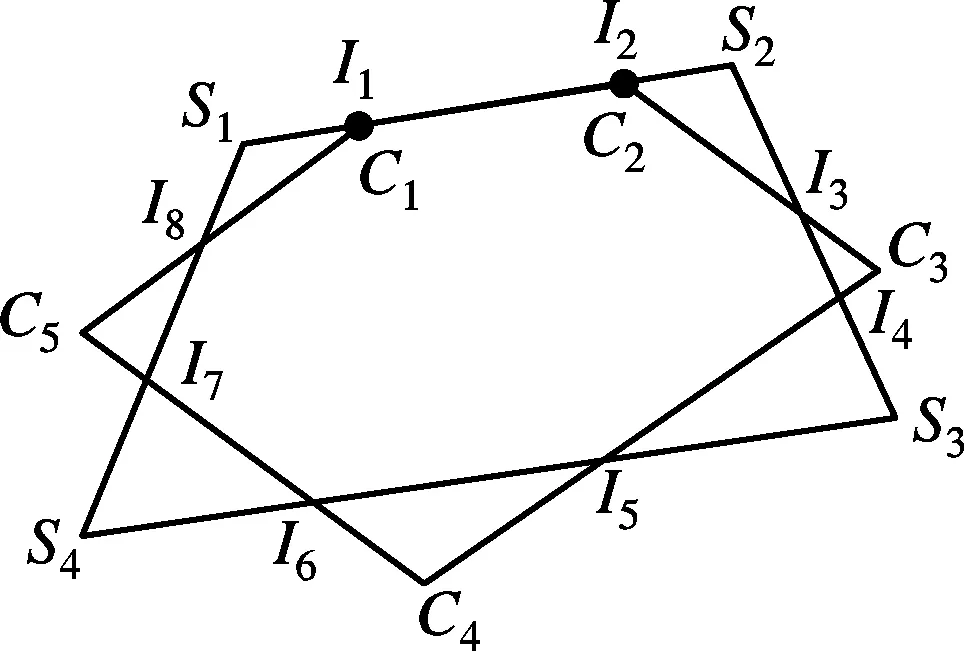
(b)
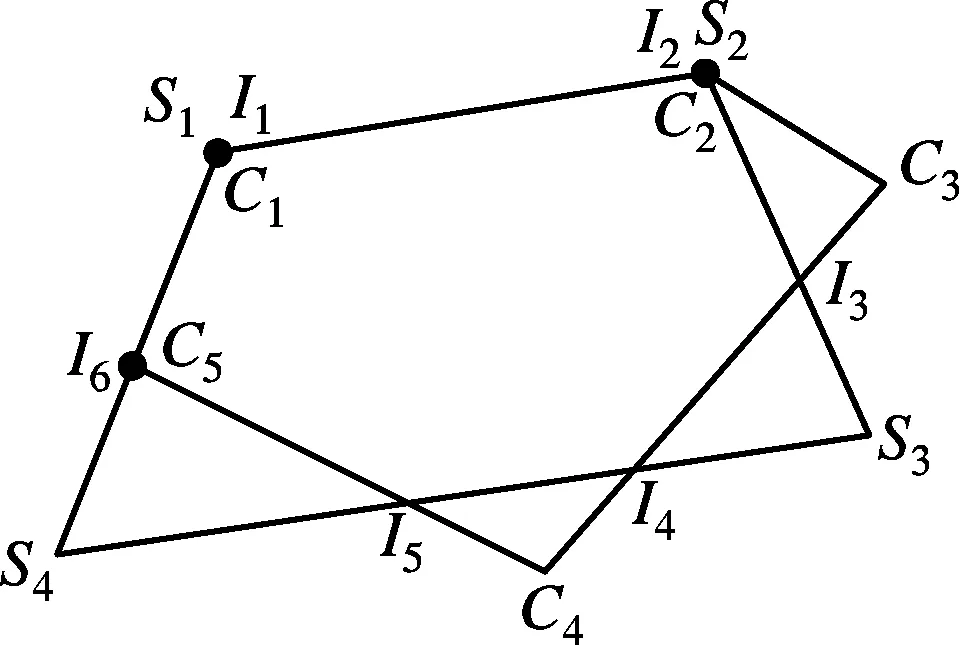
(c)
2.3.2基于交点关联线段间的交点进出性判别
2.2节中已经表明交点退化现象会导致对交点的进出性做出错误判断,本文提出基于交点关联线段间的方向关系来判别交点进出性的方法.方向关系是指在某个参考框架下,从空间一个目标到空间另一个目标的方向[9].对图5中的线段方向关系判别方法:① 判别交点Ik是否为该主多边形和裁剪多边形的顶点,如果是则通过交点的SegmentIndex得到该交点主多边形前一个顶点Sn-1和后一个顶点Sn+1,得到裁剪多边形前一个顶点Cm-1和后一个顶点Cm+1.② 以Sn-1,Sn和Sn+1为参考边,根据线段Cm-1Cm和CmCm+1与线段Sn-1Sn与SnSn+1的方向关系,判断线段Cm-1Cm和CmCm+1位于主多边形的边界、内部还是外部,进而判别出该交点的进出性.图5为部分交点与顶点重合的情况,其他重合情况可参考该方法解决.
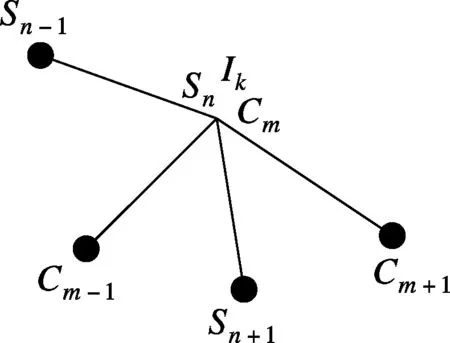
(a) (b)

(c)
3 改进的多边形裁剪算法
Greiner-Hormann算法采用双向链表的数据结构,需要存储多边形顶点前后关联点的信息,增加了数据存储量,同时双向链表的遍历操作与单向链表相比更为繁琐.因此,本文采用单向链表的数据结构实现多边形裁剪算法,减少了顶点遍历次数和求交次数,裁剪效率大幅提高.
3.1多边形交点求解
将多边形的边有规律地进行分割,被分割的边称为单调链,即具有某种相同方向关系的连续点构成的边,如图6所示将多边形A分割成4条单调链.然后采用平面扫描法求解平面线段集的交点.平面扫描法判别交点的思路是用一条垂直的扫描线段从左到右扫描过平面,在每个事件点(即线段的顶点和线段之间的交点)处修改扫描状态表,再检测相邻单调链间是否存在相交点.若检测到一个交点,则获取该线段及其交点的坐标,并将交点横坐标插入到扫描事件中[10-11].
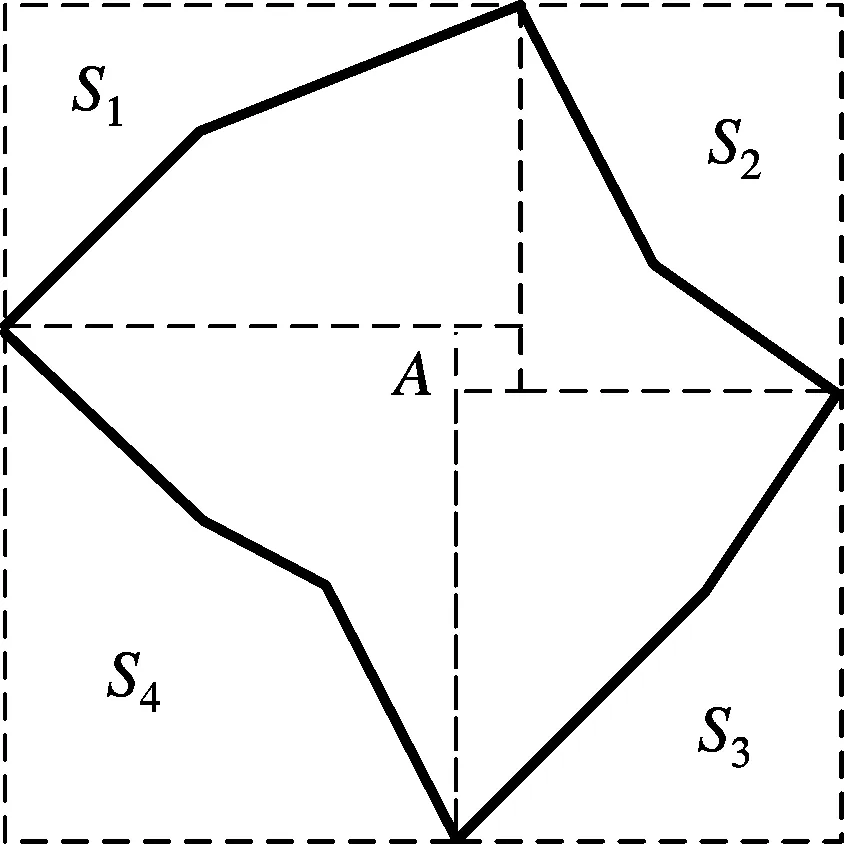
图6 多边形单调链分割图
3.2改进多边形裁剪算法流程
改进的多边形裁剪算法步骤如下:
1) 采用单向链表的数据结构将裁剪多边形C和主多边形S的外环顶点坐标按顺时针存储,内环顶点坐标按逆时针存储.
2) 按顺序对裁剪多边形C的边与主多边形S的内外环进行求交计算,求出可能存在交点的边,并确保交点坐标的唯一性.
3) 以主多边形S为参考对象,判断出将要插入到裁剪多边形C中的交点的进出性,且该交点插入到主多边形S的进出性与之相反.
4) 依据交点数据结构中距离Distance属性值是否为零,判别交点是否为多边形的顶点,进而判别是否存在重点现象.
① 如果交点存在重点现象,采用线段方向关系判别交点的进出性;
② 如果交点不是主多边形S和裁剪多边形C的顶点,则利用式(2)就可判别出交点的进出性.
5) 按顺序将交点添加到多边形顶点序列中,更新顶点序列表.
6) 交替遍历更新后裁剪多边形和主多边形顶点序列,通过顶点的进出性和添加的交点的进出性得到裁剪结果.
4 实验结果与分析
本文主要从算法有效性和执行效率2个方面进行了测试.有效性测试主要针对含有内环的复杂多边形和存在重点和重边现象的2个多边形裁剪,然后比较了Greiner-Hormann算法与本文优化裁剪算法的裁剪时间.因本文提出的改进算法采用单链表数据结构,因而链表的存储数据量、遍历顶点次数和求交次数均有所减少,内存空间消耗也会减少,所以本文未对内存消耗做进一步测试.
4.1算法有效性测试
4.1.1复杂多边形的裁剪测试
含有内环的多边形被称为复杂多边形,本文通过对含有一个内环和多个内环的主多边形进行裁剪测试,验证所提算法对复杂多边形裁剪的有效性.测试裁剪结果如图7和图8所示.实验结果表明本文算法可以实现对含有多个内环的多边形的裁剪.

(a) 裁剪数据
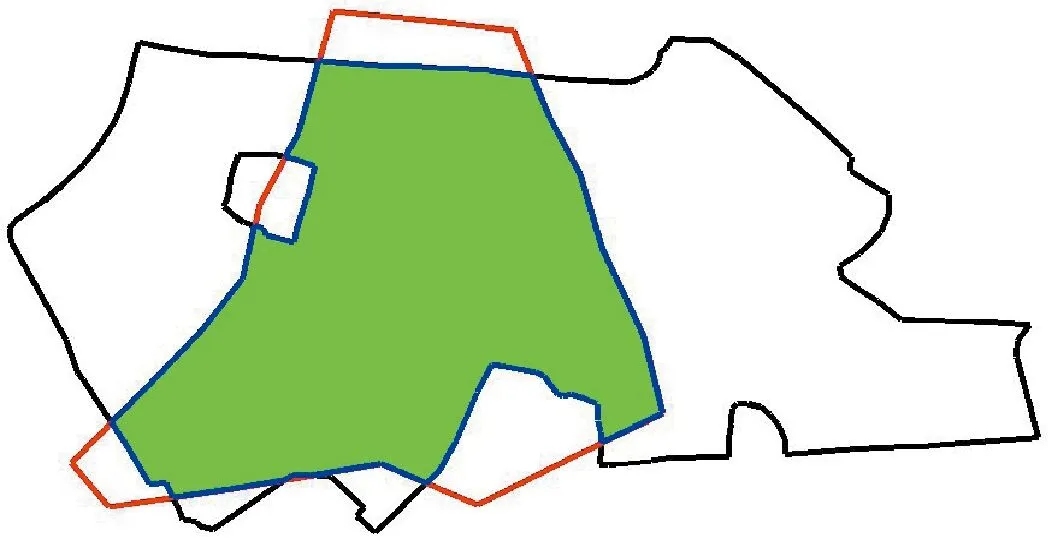
(b) 裁剪结果
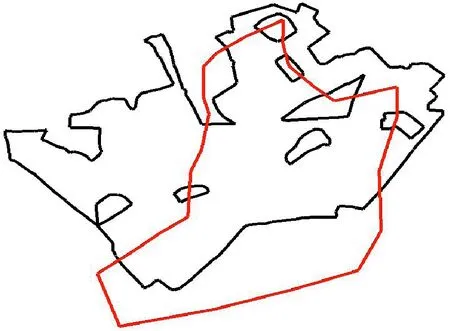
(a) 裁剪数据 (b) 裁剪结果
4.1.2含有重点和重边的多边形裁剪测试
存在重点和重边现象的多边形裁剪实验测试结果如图9和图10所示.实验结果表明在存在重点和重边的多边形裁剪中,采用基于线段方向关系判别交点进出性方法,能够得到准确的多边形裁剪结果.
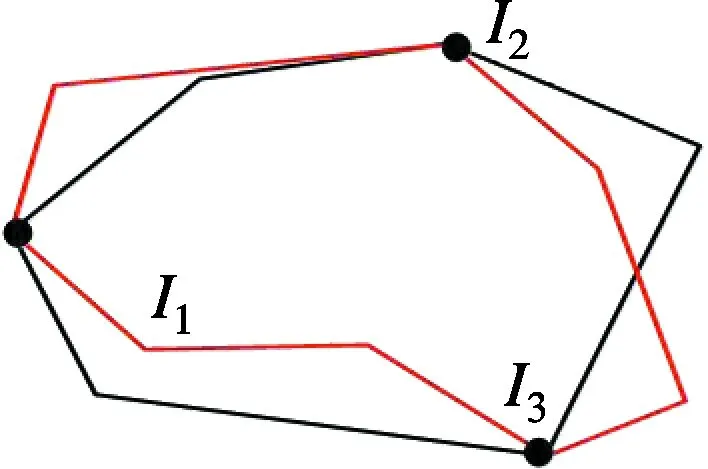
(a) 简单相交多边形 (b) 图(a)裁剪结果
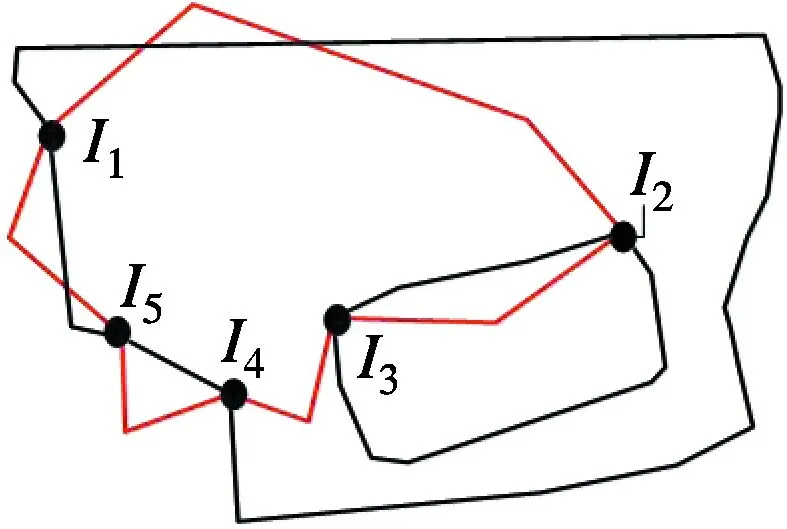
(c) 复杂相交多边形 (d) 图(c)裁剪结果

(c) 复杂相交多边形 (d) 图(c)裁剪结果
4.2算法效率测试
本文中算法效率对比测试不考虑交点退化现象.在保持交点个数不变且裁剪多边形顶点个数也不变的情况下,测试用的主多边形顶点数逐渐增加, 求得此时改进算法与Greiner-Hormann算法所消耗的时间.实验结果如表1所示.

表1 Greiner-Hormann算法与改进算法的裁剪时间比较
由表1可知, 2种裁剪算法所需要的时间均随着主多边形顶点数目的增加而增加.在顶点数和交点数相同的情况下,改进算法所需时间要少于Greiner-Hormann算法.随着主多边形顶点数目的增加,改进算法的时间消耗增加低于Greiner-Hormann算法,最终改进算法相对于Greiner-Hormann算法的时间消耗减少了接近50%.但表1中改进算法测试序列3和7不符合上述规律,即主多边形顶点个数增加时,裁剪时间并未有规律地增加.分析其原因在于这2组试验中所用的主多边形较复杂,因而被分割成较多的单调链,增加了处理时间,从而导致裁剪时间较长.
5 结语
本文在借鉴现有多边形裁剪算法的思想以及优点的基础上,优化了交点数据结构和求解方法,提出了一种快速有效的多边形裁剪算法.该算法适用于复杂的含有内环的多边形裁剪,测试表明改进算法在剪裁时间上优于Greiner-Hormann算法.其中,提出的利用交点关联线段间的分析关系来判定交点进出性的方法,能够解决存在交点退化现象的多边形裁剪问题,具有较好的实用性.
References)
[1]宋树华, 濮国梁, 罗旭, 等. 简单多边形裁剪算法[J]. 计算机工程与设计, 2014, 35(1):192-197.DOI:10.3969/j.issn.1000-7024.2014.01.036.
Song Shuhua, Pu Guoliang, Luo Xu, et al. Algorithm for simple polygon clipping[J].ComputerEngineeringandDesign, 2014, 35(1):192-197. DOI:10.3969/j.issn.1000-7024.2014.01.036.(in Chinese)
[2]Weiler K, Atherton P. Hidden surface removal using polygon area sorting[J].ACMSIGGRAPHComputerGraphics, 1977, 11(2):214-222. DOI:10.1145/965141.563896.
[3]Vatti B R. A generic solution to polygon clipping[J].CommunicationsoftheACM, 1992, 35(7):56-63.DOI:10.1145/129902.129906.
[4]Greiner G, Hormann K. Efficient clipping of arbitrary polygons[J].ACMTransactionsonGraphics, 1998, 17(2):71-83. DOI:10.1145/274363.274364.
[5]刘勇奎, 高云, 黄有群. 一个有效的多边形裁剪算法[J]. 软件学报, 2003, 14(4):845-856.
Liu Yongkui, Gao Yun, Huang Youqun. An efficient algorithm for polygon clipping[J].JournalofSoftware, 2003, 14(4):845-856.(in Chinese)
[6]张钧, 王鹏. 一种新的矢量数据多边形的快速裁剪算法[J]. 中国图象图形学报, 2008, 13(12):2409-2413.
Zhang Jun, Wang Peng. A new fast polygon clipping algorithm for vector data[J].JournalofImageandGraphics, 2008, 13(12):2409-2413.(in Chinese)
[7]王结臣, 沈定涛, 陈焱明,等. 一种有效的复杂多边形裁剪算法[J]. 武汉大学学报(信息科学版), 2010,35(3): 369-372,377.
Wang Jiechen,Shen Dingtao,Chen Yanming,et al. An efficient algorithm for complex polygon clipping [J].GeomaticsandInformationScienceofWuhanUniversity, 2010, 35(3): 369-372,377.(in Chinese)
[8]彭杰, 刘南, 唐远彬, 等. 一种基于交点排序的高效多边形裁剪算法[J]. 浙江大学学报(理学版), 2012, 39(1):107-111,122. DOI:10.3785/j.issn.1008-9497.2012.01.022.
Peng Jie, Liu Nan, Tang Yuanbin, et al. An efficient algorithm for polygon clipping based on intersection points sorting[J].JournalofZhejiangUniversity(ScienceEdition), 2012, 39(1):107-111,122. DOI:10.3785/j.issn.1008-9497.2012.01.022.(in Chinese)
[9]邓敏, 李志林, 吴静. 空间关系理论与方法[M]. 北京:科学出版社, 2013:88-110.
[10]闫浩文, 张黎明, 李茜茜, 等. 复合多边形求差的高效矢量算法[J]. 计算机应用研究, 2013, 30(10):3192-3194. DOI:10.3969/j.issn.1001-3695.2013.10.079.
Yan Haowen, Zhang Liming, Li Qianqian, et al. Vector-based efficient algorithm for computing differences between two complex polygons[J].ApplicationResearchofComputers, 2013, 30(10):3192-3194. DOI:10.3969/j.issn.1001-3695.2013.10.079.(in Chinese)
[11]Chen Z L, Ma L N, Wu L. Polygon overlay analysis algorithm based on monotone chain and STR tree in the simple feature model[C]//2010InternationalConferenceonElectricalandControlEngineering. Harbin, China, 2010: 2905-2909. DOI:10.1109/icece.2010.1420.
A high efficient polygon clipping algorithm for dealing with intersection degradation
Wang Huiqing1Chong Suwen2
(1School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China)(2Spreadtrum Communications (Shanghai) Co., Ltd., Shanghai 201203, China)
Aiming at complex polygon clipping with coincidence points and coincidence edges, a high efficient algorithm for polygon clipping is proposed for dealing with intersection degradation. The algorithm uses singly linked lists to store polygons, and acquires intersection points between polygons based on the planar scanning method with a monotone chain, thus reducing the times of traversing polygon vertices and calculating intersections. Then, it marks the entry and exit points to the clipping polygon’s interior based on the direction relationship between line segments with intersections. Finally, it updates the polygon vertex sequence and obtains cutting results. The experimental results show that the algorithm can clip a polygon with several inner rings, and obtain right clipping results even under the condition of intersection degradation. The cutting efficiency of the algorithm is significantly higher than that of the Greiner-Hormann algorithm. Therefore, it has high efficiency and practicability.
polygon clipping; intersection degradation; singly linked list; direction relationship
10.3969/j.issn.1001-0505.2016.04.005
2015-12-21.作者简介: 王慧青(1976—),女,博士,副研究员,921394420@qq.com.
“十二五”国家科技支撑计划资助项目(2013BAJ13B01).
10.3969/j.issn.1001-0505.2016.04.005.
TP391
A
1001-0505(2016)04-0702-06
引用本文: 王慧青,崇素文.一种处理交点退化现象的高效多边形裁剪算法[J].东南大学学报(自然科学版),2016,46(4):702-707.
