结构化的复合声场及其操纵颗粒有效性的实验研究
2016-09-21乔正辉
程 梅 董 卫 乔正辉
(东南大学能源与环境学院, 南京 210096)(东南大学能源热转换及其过程测控教育部重点实验室, 南京 210096)
结构化的复合声场及其操纵颗粒有效性的实验研究
程梅 董卫 乔正辉
(东南大学能源与环境学院, 南京 210096)(东南大学能源热转换及其过程测控教育部重点实验室, 南京 210096)
基于装置各部件固有频率相等的方法,设计制作了一种在平面声腔侧壁离散对称布置16极Helmholtz声源的实验装置,研究了平面声腔内由16极Helmholtz声源构造的复合声场及其对颗粒的操纵特性.通过理论和实验研究了Helmholtz声源的频率特性、平面声腔的谐振特性、平面声腔内复合声场的时空变化特性以及复合声场对平面声腔内充注的烟气颗粒操纵的有效性.结果表明:运行频率为1.805 kHz时,16极Helmholtz声源耦合的平面声腔能够实现同步谐振;平面声腔内形成了声压幅度逐渐衰减的环形复合声场;烟气颗粒被聚集在靠近壁面约0.5个波长的环形区域内,在平面声腔的中部形成了无颗粒区,颗粒聚集区与无颗粒区的面积比约为16∶9.
Helmholtz声源;共振;复合声场;烟气颗粒
驻波可以操纵气相或液相介质中微小颗粒产生有规律的变化.关于驻波声场操纵颗粒行为的特性,国内外学者进行了多方面的研究.Pathak等[1]针对声场中颗粒的团聚模型,模拟研究二氧化硅纳米颗粒悬浮液在声场中的团聚特性.Noorpoor等[2]实验研究声场脱除空气中2.5 μm细颗粒的特性,指出高强度的单频声场对微米级颗粒的脱除效率有明显提高作用.杜人君等[3]利用单轴式声悬浮系统将环己烷液滴悬浮在半空,研究空气中液滴的凝结特性.冷吟等[4]利用高速摄影仪实验表征可吸入颗粒物在驻波声场中的运动轨迹.Greenhall等[5]采用声场相变操控技术,在液体中利用驻波声场对单个颗粒进行自由连续控制.文献[6-7]提出利用2极和4极Helmholtz声源耦合谐振腔构造声场,操纵有限空间内烟气颗粒的聚散性迁移.
在光学领域对结构化光波已进行了大量深入的研究,实验中已经能够利用波的结构技术控制结构化光波的角动量和径向分布[8].借鉴结构化光波的理念,本文利用平面声腔等频率耦合多极Helmholtz声源的方法构造了复合声场,即在平面声腔内经多重声波间的相互作用形成复合声场,并通过输入端实现复合声场的角动量和径向分布的调节与控制,从而实现对颗粒的操纵.在实验中研究了该类型声场对烟气颗粒迁移行为的作用.通过理论和实验,重点研究单极和16极平面声腔的谐振特性、Helmholtz声源的频率特性、平面声腔内径向复合声场的时空变化特性以及有或无复合声场条件下烟气颗粒在平面声腔内的分布.
1 实验装置及测试系统
1.1实验装置
如图1所示,实验装置水平放置,主要由平面声腔和Helmholtz声源组成.平面声腔为封闭的正十六边形柱形声腔,侧壁中心为通孔.正十六边形的内切、外接圆半径MO和OP为平面声腔的2类特征径线,其中径线MO表征靠近无反射壁的状况,径线OP表征反射壁接缝处反射率奇异的状况.Helmholtz声源由扬声器和圆柱形Helmholtz共振器组成;Helmholtz共振器由通孔、声腔和扬声器振膜组成;扬声器为电磁式电声换能器,直径为40 mm,静态电阻为6.7 Ω.整个装置由围绕平面声腔中心、侧壁上对称布置16极的相同声源构成.Helmholtz共振器和平面声腔由有机玻璃板制成,壁厚4.5 mm.平面声腔高度为60 mm(沿z轴),小于λ/2(波长λ=192 mm).x轴方向与径线MO平行;2组等分点x2,x3,x4,x5和x7,x8,x9,x10分别沿径线MO和OP布置;x1,x6,x11为径线端点.
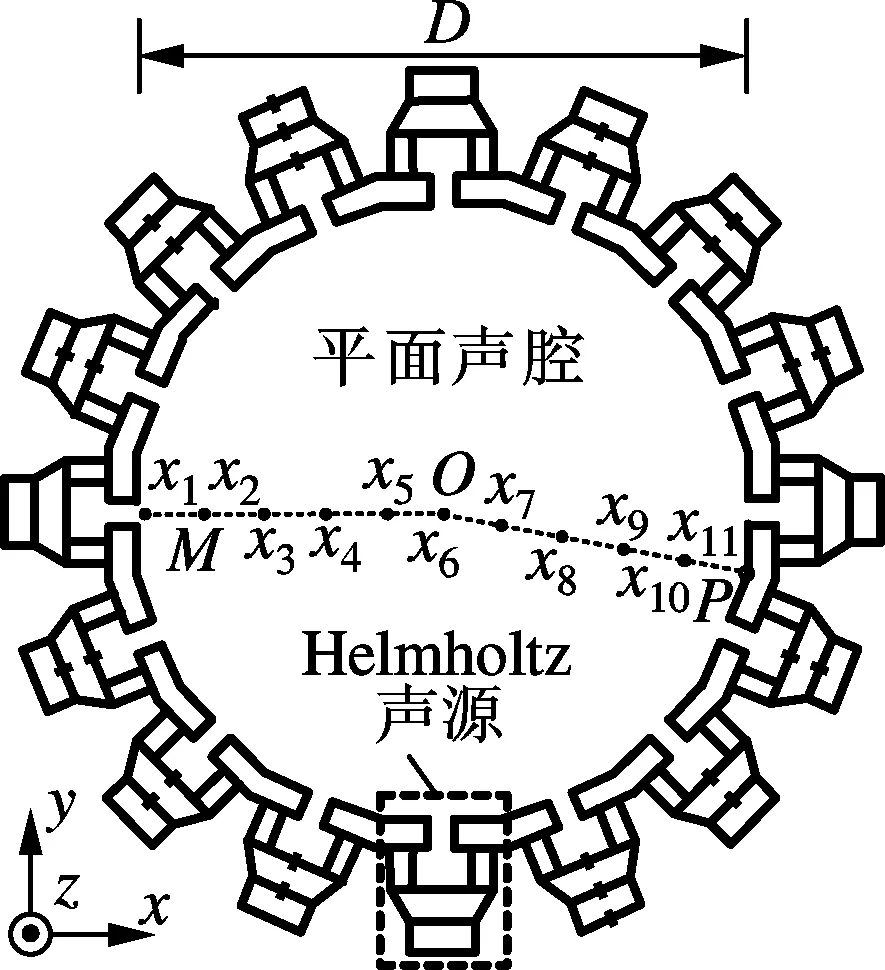
(a) 复合声场发生装置 (b) Helmholtz声源
在设计装置各声学部件的结构尺寸时,为了产生最大的声压,平面声腔和Helmholtz声源的结构固有频率满足共振相似条件,表达式为[6]
(1)
式中,f0为Helmholtz共振器的共振频率,本文中f0=1.805 kHz;D,n为平面声腔的宽度和谐振阶数,本文中取D=480 mm,n=5;c为声速,本文中c=346 m/s;de,le,dt和lt分别为通孔直径、通孔长度、声腔直径和声腔长度,分别取值为8.0,5.0,35.0和4.5 mm.
1.2实验测试系统
测试系统主要由信号发生器、功率放大器、实验装置、传声器和NI数据采集系统组成.图2为平面声腔耦合16极声源的实验测试系统.

图2 实验测试系统
信号发生器(型号SPF05)发出指定频率的周期性电信号,经DS2000功率放大器后以同相方式输入Helmholtz声源的扬声器,扬声器振膜产生的声波经Helmholtz共振器进入平面声腔,在腔内产生复合声场.声场的测压孔按照径线MO和OP上的等分点和端点布置,2组测压孔的间距分别为48.0,48.9 mm.用传声器(型号B&KMPA416)和数据采集系统(型号NIPXI-4472)同步采集各测压孔的声压.利用电脑上Labview软件对采集的声压数据进行处理和记录.由于装置结构的对称性,径线MO和OP分别属于正十六边形的2类径线,在测压孔间距不大于λ/4的条件下,2类径线上测压孔的声压能够表征平面声腔内的声场分布.
2 模型分析
2.1Helmholtz声源
2.1.1Helmholtz声源电声可调控性分析
由于Helmholtz声源的结构尺寸远小于声波波长,结合声学集中参数模型[9-10]和电磁式换能器声电转换模型[11]对Helmholtz声源进行回路分析,得到如图3所示的等效类比电路.

图3 Helmholtz声源等效类比电路图

由图3等效类比电路可得Helmholtz声源的等效电阻抗Zin的表达式为
Zin=Re+jωLe+

(2)
式中,Ze为扬声器音圈的等效电阻抗;Zmo为扬声器振膜的等效声阻抗;Za为Helmholtz共振器的等效声阻抗;ω为频率;j2=-1.Helmholtz声源的响应系数p′为Ps与U0的比值,表达式为
(3)
由式(3)可知,响应系数p′与输入电信号频率和Helmholtz声源的物理参数有关,这表明了出口声压Ps的可调属性.
2.1.2Helmholtz声源的声学特性分析
当扬声器发射的声波进入类比法布里-珀罗腔[12]的声腔时,将会产生声波的反射、相干和多重循环,所以声腔内的声场属于复合声场.类比界面上光的传输和反射[13],声波在腔内的传播如图4所示.图中,lt为反射壁1和2之间的距离,E0为入射声场,Er为反射声场,Et为声腔发射的声场,t1为声腔内循环声场的传输率,t2为经孔径向腔外的声辐射传输率,θ为声波入射角.Ecir为2个壁面间的循环声场即多重反射的回音效应.循环声场Ecir表达式为[14]
Ecir=t1E0+ejγ(-r1)(-r2)Ecir
(4)
式中,ejγ表示传播相位;r1,r2为2个壁面的反射率;γ为入射声场通过声腔往返循环聚集的相位.式(4)可简化为
(5)

图4 Helmholtz声腔声传播示意简图
基于声腔内入射声场的反射声场和发射声场的表达式为
(6a)
(6b)
腔内组合的声能可以通过Ecir的绝对值二次方计算得到,此时声能组合因数为
(7)
声辐射穿过声腔与腔壁面的反射声发生相位叠加重组,由式(7)可见:当cosγ=1,声能组合因数达到最大值,即认为声腔发生共振;当cosγ=-1,声能组合因数达到最小值,即认为声腔发生反共振.由此可知,Helmholtz声源具有与激光相似的单频率共振与反共振的双重属性.
2.2平面声腔中复合声场的构造
平面声腔侧壁离散对称布置的16极Helmholtz声源同时向平面声腔中心发射相同声波(见图1(a)),考虑平面声腔侧壁对声波的反射及多重反射的回音效应[15-16],这些效应相互交织重组,最终在平面声腔的有限空间内构成特定的复合声场.
2.3辐射声场对颗粒的作用
驻波环境中,满足特定条件下颗粒会受到声学辐射力的作用.当颗粒的尺寸远小于波长时,一旦颗粒的几何结构等效为可压缩的球形,声场对单一颗粒小球的声学辐射力F0表达式为[17]
罗永卫[9]在《广西退役运动员就业安置政策执行效果研究》中讲到,广东省在安置政策执行中存在诸多问题,包括就业渠道不畅、政策制定滞后与落实不到位、运动员缺乏职业生涯规划等问题。他希望通过发挥政府的主导作用,拓展多元化就业模式、以市场为导向,完善政策保障,实现退役运动员就业安置政策与市场经济发展的完美结合。
F0=-(2πA2Vcβwλ-1)ψ(β,ρ)sin(2kx)
(8a)
(8b)
式中,A为声压幅值;Vc为颗粒体积;β和ρ为可压缩系数和密度;下标c和w分别表示空气媒介与颗粒;k为波数;比例因子ψ与媒介和颗粒的可压缩系数及密度有关.当ψ(β,ρ)>0时,声场对颗粒的声学辐射力指向驻波波节;当ψ(β,ρ)<0时,声场对颗粒的声学辐射力指向驻波波腹.
3 实验测试与分析
3.1Helmholtz声源的频率特性
Helmholtz共振器作为一种声学元件,其声学参量Ma,Ra和Ca的表达式为[18]
(9a)
(9b)
(9c)
结合式(1)中Helmholtz共振器的尺寸参数,利用式(9)计算Helmholtz共振器的各声学参数,其中ρw=1.205 kg/m3.实验[19]测得扬声器参数如下:Le=3.32×10-4H,Rmo=1.62×10-2Ω,Mmo=4.3×10-6kg,Cmo=2.09×10-3m/N和φ=0.412.
利用式(3)模拟Helmholtz声源响应系数随输入电信号频率的变化曲线;同时向单极Helmholtz声源输入电压有效值为0.13 V、频率为0.8~2.4 kHz的正弦交流电信号,得出声源声压随频率的响应规律,结果如图5所示.由图可知,响应系数和声压的最大峰值都出现在1.805 kHz处,因而Helmholtz声源的最佳谐振频率在理论和实验上是一致的.

图5 声源频率特性
3.2平面声腔的谐振特性
测试时,向耦合平面声腔的任一单极Helmholtz声源和全部16极Helmholtz声源分别输入电压有效值为0.33 V、频率为0.3~2.4 kHz的正弦交流电信号.图6为单极和16极声源作用下平面声腔内径线MO上各测试位置声压随频率变化的响应特征.

(a) 单极声源

(b) 16极声源
由图6(a)可知,单极声源作用下各测试位置声压随频率的变化具有相似性,存在多个离散分布的峰值区域,峰值区域对应频率带宽在各测试位置近似相同,平面声腔的整个空间内存在多个离散的谐振频率.在频率1.5~2.1 kHz对应的峰值区域内,声压响应峰值不具有唯一性,该区域内的频率带宽明显较其他峰值区域大,说明该区域内单极声源作用下平面声腔的谐振特征比较模糊,单极声源辐射的声波在平面声腔内激发的谐振特性不明显.
由图6(b)可知,16极声源作用的平面声腔仅在中心频率为0.9,1.8 kHz的2个频率区域产生2个孤立陡峭的声压尖峰,峰值区域集中,尖峰最小声压与单极声源作用产生的最大声压一致,尖峰最大声压约是单极声源的3.0(59.5/20≈3.0)倍.说明在这2个频率条件下,相比单极声源,16极声源作用下平面声腔的谐振特性更强烈,16束辐射声波在平面声腔内构造了明显的复合声场.平面声腔在1.8 kHz频率产生的响应声压约是在0.9 kHz频率产生声压的2.3(59.5/26≈2.3)倍.在测试谐振特性的频率范围内,装置在频率1.8 kHz处产生的声压最大,该频率近似等于通过式(1)设计的理论频率1.805 kHz.对比图5和图6(b)可知,平面声腔和Helmholtz声源的最佳谐振频率基本一致,共振频率均为1.805 kHz,装置的2类声学部件平面声腔和Helmholtz声源发生了最佳频率耦合.
3.3平面声腔内声场的时空分布
同时向16极Helmholtz声源输入电压有效值为0.33 V,频率分别为1.70,1.75,1.80,1.85和1.90 kHz的正弦交流电信号,测试平面声腔内声场的时间和位置分布特征,结果如图7所示.

(a) 随时间变化(径线MO) (b) 随时间变化(径线OP)

(c) 随位置变化(径线MO) (d) 随位置变化(径线OP)
由图7(a)和(b)可知,平面声腔2类径线上各测点的声压随时间均呈正弦周期性变化.平面声腔中心x6处的声压最高,位于强声场区域;径线MO上x2,x4处和径线OP上x8,x10处的声压最低,位于弱声场区域.径线MO上,x1,x5,x6处的波动相位近似相等,相差0相位;与x3,x4处波动相位相反,相差π相位;与x2处波动相位相差π/2.径线OP上,x6,x7,x10处的波动相位相同;与x8,x9处波动相位相反.由此可知,在同一时间变化周期内,平面声腔内各位置声压波动可以同时达到最大值或最小值.这种时间变化特征说明16极声源注入的声场在相互作用过程中会产生同时增强或同时削弱的效果,这种特性有利于构造稳定的复合声场.
图7(c)和(d)分别为在不同频率时平面声腔径线MO和OP上的声压变化曲线.由图可知,在1.80,1.85和1.90 kHz的频率条件下,对应产生的3条声压变化曲线逐渐重合,测压孔xi(i=1,2,…,11)越靠近壁面,曲线之间的差异性越大;1.80 kHz对应的声压值曲线整体略高于其他2条声压值曲线,而1.75,1.70 kHz频率产生的声压值明显低于前3条曲线的声压值,说明在各声学部件耦合频率1.80 kHz的谐振条件下,16极声源激发平面声腔产生的复合声场起伏性最佳,声场质量最好.在2类径线上,x2,x4,x8,x10的声压为极小值,处于曲线谷值;x3,x6,x9的声压为极大值,处于曲线峰值.
从平面声腔中心到侧壁面,2类径线上声压逐渐起伏衰减,且径线上到中心的距离相同时,声压近似相等.平面声腔内的复合声场以腔心O为圆心在逐渐远离腔心方向形成近似等压力圆环线的声场.圆环形声场分布呈现中间声压力变化最强,向周围逐渐弛豫衰减趋势.这种声场环形分布的起伏特性与文献[20]利用16极直径为10.98 mm的环形面声源在液体媒介液面用2.45 MHz超声波激发的表面驻波类似.由于液体和空气物理特性的差异,点/面声源向媒介辐射声波的阻抗匹配存在明显差异,液体/空气媒介的声学装置不能互用.在忽略点/面声源结构、声波频率和媒介阻抗差异的条件下,本文实验得出的声场空间分布结果与文献[20]中利用贝塞尔函数模拟的声场分布近似,说明本文中由16极声源叠加构成的复合声场可以用贝塞尔函数方法模拟.
3.4复合声场操纵烟气颗粒实验
Vranjes等[21]在分析能量密度梯度时指出:能量分布不均的流体中,粒子倾向于向低能态迁移或直接扩散至低能量密度区.有限空间内能量分布形态反映出区域的内部动力学特征[22].
向密封平面声腔内注入烟草燃烧烟气颗粒,烟气体积为52.8 L.通过TSI9303粒子计数器测得烟气中69%的颗粒粒径不大于0.3 μm,31%的颗粒粒径范围为0.3~2.5 μm.无声场作用时,平面声腔内的烟气在光束S1和S2下呈近似乳白色均匀分布(见图8(a)).向16极Helmholtz声源输入电压有效值为4.7 V、频率为1.805 kHz的正弦交流电信号,20 min后平面声腔内的烟气分布如图8(c)所示.

(a) 无声场 (b) 局部放大
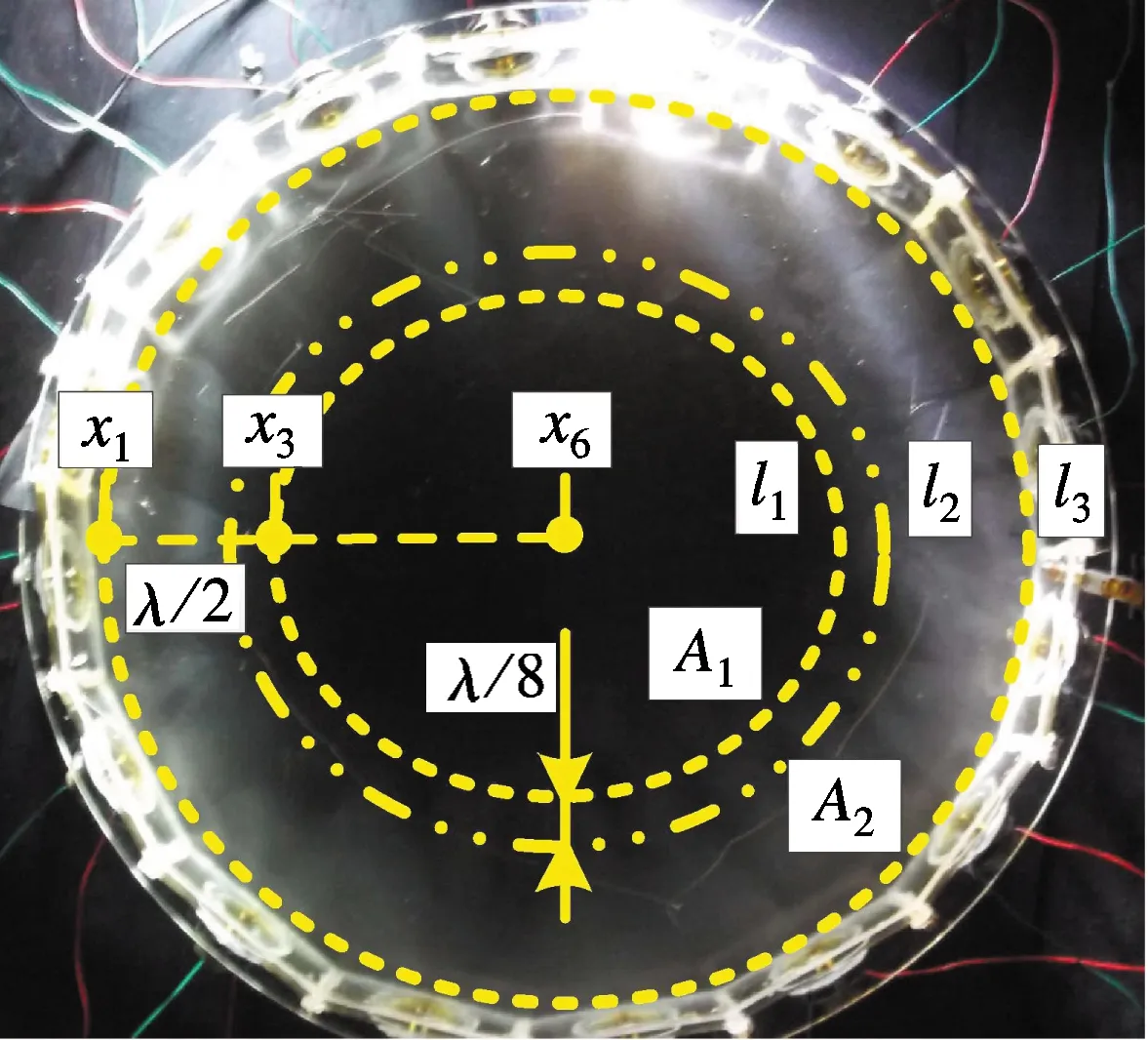
(c) 有声场
由3.3节可知,平面声腔内的复合声场中中间声场强度明显高于边缘,产生了复合密度梯度场.根据式(8)可知,在密度梯度场的作用下,大量烟气颗粒从靠近中心的强声场区域向靠近边缘的弱声场区域迁移,最终聚集在靠近壁面的弱声场环形区域内.从而导致声腔中部烟气颗粒分布稀薄,形成近似无颗粒区.
由图8(c)平面声腔内整体的声能密度和烟气颗粒密度分布表明,在复合声场中,平面声腔内的烟气颗粒产生了明显的聚集分布.图中,圆线l1,l2,l3界定了颗粒聚集分布区域的边界,圆线l1(半径r1≈3λ/4)内部为无烟气颗粒区域A1,圆环l2~圆环l3(宽度l2-3≈3λ/8)内部为烟气颗粒聚集区,圆环l1~圆环l2(宽度l1-2≈λ/8)内部为有或无烟气颗粒的过渡区,过渡区烟气颗粒明显少于外部颗粒聚集区而多于内部无颗粒区.相对无颗粒区,烟气颗粒聚集区和过渡区可划为同一颗粒聚集区A2,位于圆环l1~圆环l3(宽度l1-3≈λ/2)内部.区域A2和A1的面积分别为((5λ/4)2-(3λ/4)2)π≈1 157.5 cm2和(3λ/4)2π≈651 cm2,区域A2与A1的面积比约为16∶9.
在圆环l2~圆环l3呈现的白色烟气颗粒聚集区内,围绕壁面16极声源形成以细窄暗条纹分割的16个近似孤立的烟气颗粒聚集团.图8(b)局部展示了烟气颗粒聚集团的具体结构.图中的细窄暗条纹内无烟气颗粒,条纹位于2块反射板的接缝处.
该实验验证了持续输入的声学辐射能量在平面声腔的几何中心聚集形成高密度声场,并同时沿径向朝边缘扩展,从而构成了声场密度的几何结构.此外,随着声场密度的扩张,挤压了烟气颗粒存在的空间.在扩张的声学密度场作用下,烟气颗粒聚集在声场密度较低的空间,从而构造了看似有结构的声场与烟气颗粒密度分布.
4 结论
1) 利用共振相似条件设计装置,各声学部件能够达到最佳频率耦合.在信号频率1.805 kHz的作用下,平面声腔和Helmholtz声源能够产生同步谐振,通过输入端可以实现复合声场的角动量和径向分布的调节与控制.
2) 空间对称的16极Helmholtz声源向平面声腔内发射的相同声波经交织重组后,形成中间声场强度高、边缘声场强度低的环形复合声场.在装置固有共振频率附近,输入信号的频率小幅改变后,产生的复合声场结构能够近似不变.
3) 与无声场作用相比,烟气颗粒在平面声腔的复合声场挤压下,以环形方式聚集在声腔边缘.颗粒聚集区的面积约为1 157.5 cm2,无颗粒区的面积约为651 cm2,验证了复合声场操纵烟气颗粒的有效性.
References)
[1]Pathak B, Deepu P, Basu S, et al. Modeling of agglomeration inside a droplet with nanosuspensions in an acoustic field[J].InternationalJournalofHeat&MassTransfer, 2013, 59(2): 161-166.
[2]Noorpoor A R, Sadighzadeh A, Habibnejad H. Influence of acoustic waves on deposition and coagulation of fine particles[J].InternationalJournalofEnvironmentalResearch, 2013, 7(1): 131-138.
[3]杜人君,解文军.声悬浮条件下环己烷液滴的蒸发凝固[J].物理学报,2011,60(11):394-399.
Du Renjun, Xie Wenjun. Evaporation induced solidification of cyclohexane drops under acoustic levitation condition[J].ActaPhysicaSinica, 2011, 60(11): 394-399. (in Chinese)
[4]冷吟,赵兵,姚刚,等.可吸入颗粒物在驻波声场中运动的可视化研究[J].工程热物理学报,2007,28(S1):209-212.
Leng Yin, Zhao Bing, Yao Gang, et al. Visualization research on inhalable particles in a standing wave acoustic field[J].JournalofEngineeringThermophysics, 2007, 28(S1): 209-212. (in Chinese)
[5]Greenhall J, Vasquez F G, Raeymaekers B. Continuous and unconstrained manipulation of micro-particles using phase-control of bulk acoustic waves[J].AppliedPhysicsLetters, 2013, 103(7): 0741037-01-0741037-04. DOI:10.1063/1.4819031.
[6]乔正辉,黄亚继,董卫.对称Helmholtz声源圆柱形波导的声学谐振特性[J].东南大学学报(自然科学版),2014,44(3):579-584. DOI:10.3969/j.issn.1001-0505.2014.03.023.
Qiao Zhenghui, Huang Yaji, Dong Wei. Acoustic resonance characteristics of symmetric cylindrical waveguide with Helmholtz sound source[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2014, 44(3): 579-584. DOI:10.3969/j.issn.1001-0505.2014.03.023. (in Chinese)
[7]Qiao Z H, Huang Y J, Vincenzo N, et al. Aerosol manipulation by acoustic tunable phase-control at resonant frequency[J].PowderTechnology, 2015, 281: 76-82. DOI:10.1016/j.powtec.2015.04.081.
[8]Harris J, Grillo V, Mafakheri E, et al. Structured quantum waves[J].NaturePhysics, 2015, 11(8): 629-634. DOI:10.1038/nphys3404.
[9]王泽锋,胡永明,孟洲,等.水下圆柱形Helmholtz共振器的声学特性分析[J].物理学报,2008,57(11):7022-7029.
Wang Zefeng, Hu Yongming, Meng Zhou, et al. Acoustic characteristics of underwater cylindrical Helmholtz resonator[J].ActaPhysicaSinica, 2008, 57(11): 7022-7029. (in Chinese)
[10]周城光,刘碧龙,李晓东,等.腔壁弹性对充水亥姆霍兹共振器声学特性的影响:圆柱形腔等效集中参数模型[J].声学学报,2007,32(5):426-434. DOI:10.3321/j.issn:0371-0025.2007.05.006.
Zhou Chengguang, Liu Bilong, Li Xiaodong, et al. Effect of elastic cavity walls on acoustic characteristics of a water-filled Helmholtz resonator: equivalent lumped parameter model for cylindrical cavity[J].ActaAcoustic, 2007, 32(5): 426-434. DOI:10.3321/j.issn:0371-0025.2007.05.006. (in Chinese)
[11]姚丽,董卫,吴仲武.一种电磁式声电换能器的特性研究[J].电声技术,2013,37(1):33-38. DOI:10.3969/j.issn.1002-8684.2013.01.008.Yao Li, Dong Wei, Wu Zhongwu. Characteristic research on electromagnetic acoustic-electric transducer[J].AudioEngineering, 2013, 37(1): 33-38. DOI:10.3969/j.issn.1002-8684.2013.01.008. (in Chinese)
[12]Song K, Kim K, Hur S, et al. Sound pressure level gain in an acoustic metamaterial cavity[J].ScientificReports, 2014, 4: 7421-01-7421-06. DOI:10.1038/srep07421.
[13]Shantanu D, Sougata C, Amitesh K, et al. A new mechanics of corpuscular-wave transport of momentum and energy inside negative indexed material[J].FundamentalJournalofModernPhysics, 2011, 1(2): 223-246.
[14]Jason S P. Radiation pressure effects in a suspended Fabry-Perot cavity[D]. Cambridge, Massachusetts, USA: Massachusetts Institute of Technology, 2006.
[15]Panigrahi R, Srivastava S K. Trapping of microwave radiation in hollow polypyrrole microsphere through enhanced internal reflection: A novel approach[J].ScientificReports, 2015, 5: 7638-01-7638-10. DOI:10.1038/srep07638.
[16]van Duong T, Chen R, Sun H D. Tuning whispering gallery mode lasing from self-assembled polymer droplets[J].ScientificReports, 2013, 3: 1362-01-1362-05. DOI:10.1038/srep01362.
[17]Skotis G D, Cumming D R S, Roberts J N, et al. Dynamic acoustic field activated cell separation[J].LabonaChip, 2015, 15(3): 802-810. DOI:10.1039/c4lc01153h.
[18]马大猷.亥姆霍兹共鸣器[J].声学技术,2002,21(1/2):2-3.
Ma Dayou. Helmholtz resonator[J].TechnicalAcoustic, 2002, 21(1/2): 2-3. (in Chinese)
[19]马大猷.声学手册[M].修订版.北京:科学出版社,1983:288-289.
[20]Courtney C R P, Drinkwater B W, Demore C E M, et al. Dexterous manipulation of microparticles using Bessel-function acoustic pressure fields[J].AppliedPhysicsLetters, 2013, 102: 12350812-01-12350812-05. DOI:10.1063/1.4798584.
[21]Vranjes J, Kono M. Energy in density gradient[J].PhysicsofPlasmas, 2015, 22: 0121051-01-0121051-06.
[22]Kim T H, Yoon J, Baek S H, et al. Energy landscape scheme for an intuitive understanding of complex domain dynamics in ferroelectric thin films[J].ScientificReports, 2015, 5: 11625-01-11625-10.
Experimental study on structured complex acoustic field and its effectiveness of particle manipulation
Cheng Mei Dong Wei Qiao Zhenghui
(School of Energy and Environment, Southeast University, Nanjing 210096, China)(Key Laboratory of Energy Thermal Conversion and Control of Ministry of Education, Southeast University, Nanjing 210096, China)
Based on the method with equal natural frequencies for all equipment components, an experimental device symmetrically and discretely distributed by 16 Helmholtz sound sources (HSSs) on the sidewall of a planar acoustic cavity was designed and fabricated. The complex acoustic field created by 16 HSSs in the cavity and its manipulation on particle were studied. The frequency characteristics of HSS, the resonance of planar acoustic cavity, the time-space variation feature of acoustic field and its manipulating effectiveness on filling smoke particles in planar acoustic cavity were theoretically and experimentally researched. The results show that the synchronization resonance of planar acoustic cavity coupled to 16 HSSs occurs at the working frequency 1.805 kHz. An amplitude-decaying annular complex acoustic field is generated in planar acoustic cavity. Smoke particles are gathered in the annular region about 0.5 a wavelength near the wall. There forms a particle-free zone in cavity central, and the area ratio of particle clusters to no particles is about 16∶9.
Helmholtz sound source; resonance; complex acoustic field; smoke particles
10.3969/j.issn.1001-0505.2016.04.008
2015-11-01.作者简介: 程梅(1990—),女,硕士生;董卫(联系人),男,博士,教授,dongwei59@seu.edu.cn.
中央高校基本科研业务费专项资金资助项目(3203005101)、江苏省普通高校研究生科研创新计划资助项目(KYLX15_0069).
10.3969/j.issn.1001-0505.2016.04.008.
TK09
A
1001-0505(2016)04-0720-07
引用本文: 程梅,董卫,乔正辉.结构化的复合声场及其操纵颗粒有效性的实验研究[J].东南大学学报(自然科学版),2016,46(4):720-726.
