简易布窗帘及课桌对教室空场混响时间的影响
2016-09-21郭文成黄功俊闵鹤群
郭文成 黄功俊 闵鹤群
(1东南大学建筑学院, 南京 210096)(2东南大学城市与建筑遗产保护教育部重点实验室, 南京 210096)(3东南大学土木工程学院, 南京 210096)
简易布窗帘及课桌对教室空场混响时间的影响
郭文成1,2黄功俊3闵鹤群1,2
(1东南大学建筑学院, 南京 210096)(2东南大学城市与建筑遗产保护教育部重点实验室, 南京 210096)(3东南大学土木工程学院, 南京 210096)
采用实验测量和数值仿真研究了常用简易布窗帘及课桌对国内大学典型教室空场混响时间的影响规律和机理.首先,选取了尺寸为16.8 m×10.2 m×3.78 m的新建教室,分别在未安装窗帘和课桌、仅安装窗帘、已安装窗帘和课桌等多种状态下,使用中断声源法对其空场混响时间进行了实验测量.然后,基于Raynoise建立了该教室上述多种状态下的声场仿真模型.将仿真结果与实验测量结果进行对比,推算出了该教室各内表面、窗帘和课桌的吸声系数.结果表明,窗帘主要通过吸声而课桌则通过吸声以及几何结构来改变教室混响,并且窗帘和课桌可分别使该教室空场混响时间至少降低54%和27%.
教室;吸声;混响时间;噪声控制;声舒适
教室听闻环境的好坏直接影响课堂教学质量,因此相关问题一直是国内外建筑声学领域研究的热点[1-2].语言清晰度作为评价教室听闻环境的重要指标之一,受到混响时间以及早后期声能比的影响,例如当混响时间过高时,早后期声能比减小,导致语言清晰度降低,教室听闻环境恶化[3-4].因此,理想的混响时间是教室获得良好声舒适度的重要条件.
Hodgson等[5]研究了获得良好语言清晰度所需的最佳混响时间,考虑了语言声源和噪声源同时存在于教室这一更接近实际的情况,得出当信噪比在20 dB以上时,各类体积的教室最佳混响时间在0.1~0.9 s之间的结论.宋拥民等[6]借助虚拟声环境的方法,对不同混响条件的教室语言清晰度进行了分析,结果表明,在高信噪比条件下,体积不超过200 m3的教室的中频混响时间控制在0.6 s左右时,室内的听闻环境最佳.我国相关标准针对不同类别的教室,给出了不同的空场混响时间建议值,如:普通教室体积小于200 m3时空场混响时间不大于0.8 s,体积大于200 m3时空场混响时间不大于1.0 s[7].
然而,大部分教室的混响时间实际上并未达到建议值.Tang等[8]对香港18所中小学教室的空场混响时间进行了现场测量,发现大部分教室的中频混响时间(500,1 000,2 000 Hz的混响时间的算术平均值)均大于0.8 s,其中实验类教室达到了1.5 s.李杰等[9]对某大学18间新建和已有教室的空场混响时间进行了测量,结果均在1 s以上,部分教室甚至在2 s以上.针对国内学校教室空场混响时间过长这一普遍现象,探讨相应的简易但有效的措施进行控制显得十分必要.Shield等[10]研究了英国中学教室声环境,发现吸声吊顶比地毯对改善混响时间效果更佳.Peng 等[11]详细讨论了天花板附加吸声吊顶对广州某小学教室混响时间的影响,发现吸声吊顶可使早期衰变时间和混响时间均下降50%左右,从而提高了语言清晰度.
上述围绕教室混响时间改善措施的研究都集中于研究吸声吊顶、地毯等附加吸声材料的措施效果,均需要在教室中进行额外的声学装修.若能通过更换教室中已有的典型内饰(如窗帘、桌椅等)对空场混响时间加以有效的控制,则将大大降低建设成本与实现难度.本文将研究典型大学教室中简易布窗帘(一般指布置方式简单的布艺窗帘,如主要面料为棉类或者聚酯纤维的窗帘,如无特殊说明,下文所称窗帘均指简易布窗帘)和课桌对教室空场混响时间的影响规律,并讨论可能的机理,以期为控制教室混响时间提供一种简易且有效的方法.
1 实验测量分析
1.1实验布置
测量对象为某大学的典型教室,其平面图如图1所示,教室尺寸为16.8 m×10.2 m×3.78 m,内表面积约546.8 m2,体积约为647.7 m3.教室内墙面和天花板均为普通抹灰,墙面已安装平开玻璃窗,地板为光滑釉质瓷砖满铺,此外还有6幅窗帘和70张课桌.教室内分3类吸声单元:① 墙面(包括玻璃窗和门,见图1中C1~C9和M1,M2,在测量过程中均为关闭状态)和天花板抹灰;② 窗帘,为普通布艺窗帘,面料为100%聚酯纤维(涤纶),表面较为光滑无条纹;③ 课桌,其主要材质为密度板,表面平整并喷涂有白色面漆.为简化问题,地板按声学刚性表面处理,即假定吸声系数为0.
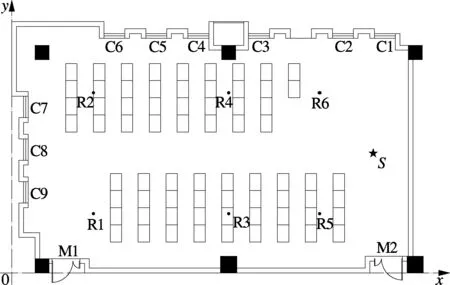
图1 实验测量的房间平面以及声源点和测点分布示意图
实验测量过程中共设置了6个测点R1~R6均匀地分布在教室平面,为准确定位测点位置,以教室左下角为坐标原点,以教室宽度方向为y轴,以教室长度方向为x轴构建直角坐标系.R1~R6的高度均为1.2 m,在x-y平面的坐标分别为(3.5, 2.5),(3.5, 7.6),(9.3, 2.5),(9.3, 7.6),(13.2, 2.5),(13.2, 7.6) m.S为声源位置,高度为0.5 m,x-y平面坐标为(15.5, 5.05) m.
采用中断声源法[12]测量混响时间.测量设备照片如图2所示,扬声器为丹麦B& K 4224型有源扬声器,声源信号为白噪声,声压级为95 dB且测量过程中保持不变,现场本底噪声水平为43 dB,声源信号高于噪声信号52 dB,因此可通过测量RT30来分析混响时间.传声器为GRAS-26CA型自由场传声器.测量过程中,声信号的产生和中断由法国01dB-Symphonie双通道声学测试分析系统控制.传声器负责采集声信号并反馈回该系统,系统同时对2个通道接收的声信号的声压级衰减曲线进行分析,进而计算得到混响时间.

图2 测量设备
1.2实验测量结果
为了获得准确的测量结果,每个测点的混响时间取3次测量结果的平均值,再取6个测点混响时间的算术平均值作为教室的有效混响时间.为了研究未安装窗帘和课桌、仅安装窗帘、已安装窗帘和课桌等状态下教室的空场混响时间,共定义了如下测量实例(见图3):① 教室无窗帘和课桌;② 教室有窗帘且呈收起状态,无课桌;③ 教室有窗帘且呈全展开状态,无课桌;④ 教室有窗帘且呈收起状态,有课桌;⑤ 教室有窗帘且呈全展开状态,有课桌.混响时间的测量结果如图4所示,中频混响时间(即500,1 000,2 000 Hz倍频带混响时间的算术平均值)的测量结果如表1所示.

(a) 实例① (b) 实例②

(c) 实例③ (d) 实例④

(e) 实例⑤ (f) 窗帘近景
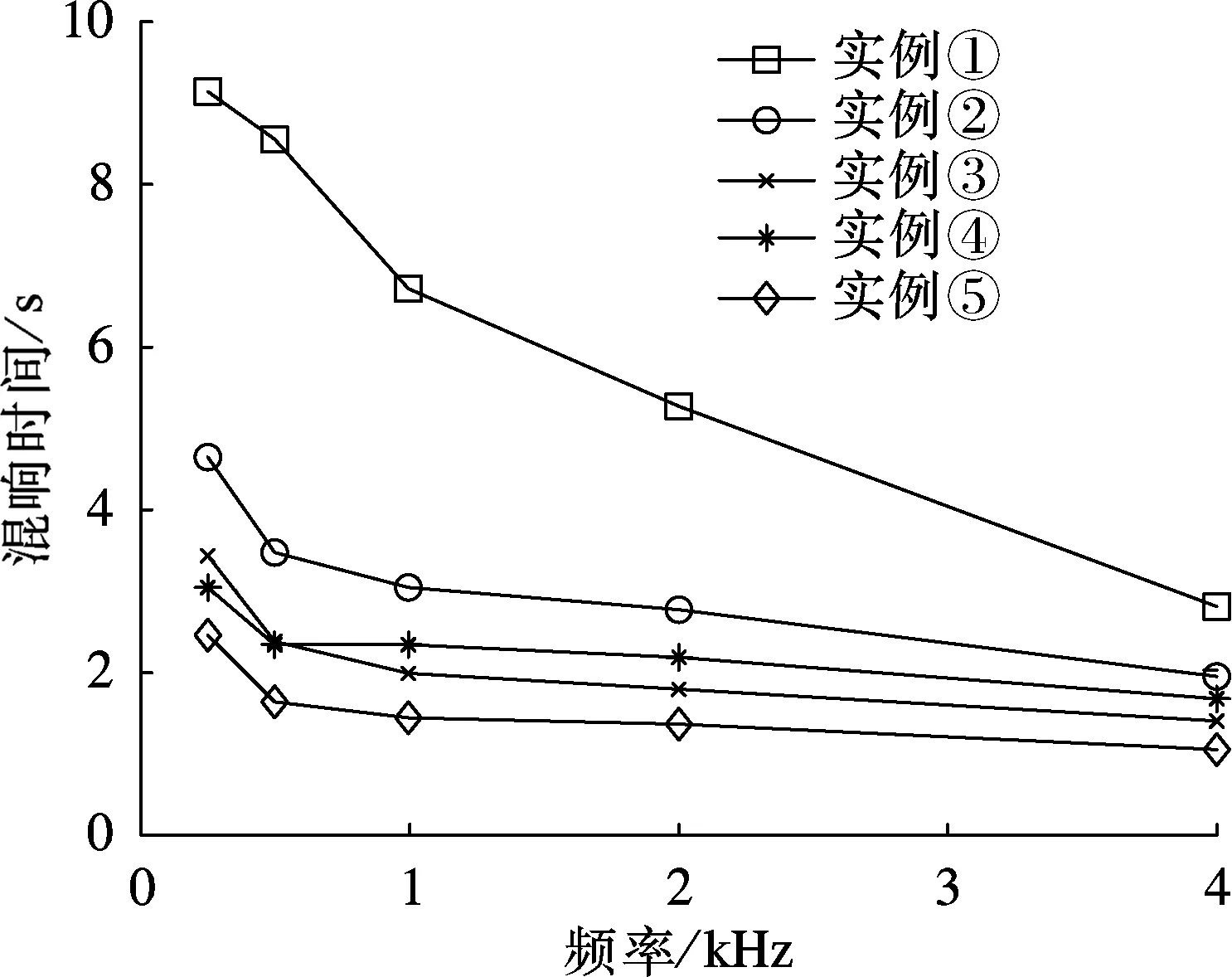
图4 实验测量的教室空场混响时间

实例实例描述中频混响时间/s①无窗帘,无课桌6.83②有窗帘收起,无课桌3.09③有窗帘展开,无课桌2.03④有窗帘收起,有课桌2.26⑤有窗帘展开,有课桌1.46
从图4和表1可看到,实例①混响时间最长,中频混响时间为6.83 s,远大于建议值,此时室内只有吸声系数很低的墙面和天花板吸声,导致混响时间过长.实例⑤混响时间最短,中频混响时间为1.46 s,虽仍高于建议值,但相比实例①改善了近78.6%,可见窗帘和课桌即使简易,也对教室空场混响时间产生了明显的改善效果.
对比实例①~③的结果可以发现:窗帘收起时能使教室空场混响时间降低54%以上;窗帘完全展开时,可使教室空场混响时间降低70.3%,效果明显.而对于课桌来说,对比实例②与实例④的结果发现,在窗帘为收起状态时,有课桌可使混响时间降低27%;对比实例③与实例⑤的结果发现,在窗帘为展开状态时,有课桌可使混响时间降低28%,两组结果很相近.上述测量结果显示,窗帘和课桌对于降低新建教室空场混响时间均有明显效果,且窗帘的效果更佳.
2 数值仿真分析
2.1仿真模型
为进一步研究简易窗帘和课桌对教室空场混响时间的影响规律和机理,本文将借助数值仿真模型进行参数分析与讨论.由于该教室的长度与高度的比值约为4.6,已经具备扁平化空间的特征,室内不满足扩散声场条件,传统的赛宾公式和伊林公式已无法适用于求解该教室的混响时间[13].因此,本文将采用比利时LMS公司开发的基于虚源法和声线追踪法的声学商业软件Raynoise3.0进行教室声场的仿真分析,该软件已被应用于建筑声学的研究工作[14-15],其算法已被证实具有较好的准确度.采用Raynoise3.0建立的教室几何模型如图5所示,声源定义为相干声源,教室的尺寸、课桌和窗帘的布置位置及尺寸均与实际情况保持一致.

图5 教室仿真分析的几何模型
2.2参数校核
参数校核的目的是通过仿真结果与实验结果的验证与对比,推算出未知吸声单元(如教室墙面、天花板、窗帘、课桌等)的吸声系数范围.校核的方法为分别建立实验测量实例①~⑤的仿真模型,调整各个吸声单元的吸声系数,直至使混响时间的仿真计算结果逼近于实验测量结果为止.校核步骤为:
① 建立没有窗帘和课桌的教室仿真模型,对应现场测量实例①.此时唯一的吸声单元便是墙体和天花板抹灰层,保持其他参数设置不变,仅变化抹灰层各倍频程的吸声系数,直到仿真预测的混响时间与实验测量混响时间误差在10%以内,此时得到的墙面与天花板抹灰层表面平均各倍频程的吸声系数即作为最终预测值.
② 建立有窗帘、没有课桌的教室仿真模型,对应现场测量实例②和③.抹灰层的吸声系数采用步骤①的最终预测值,仅变化窗帘各倍频程的吸声系数,使仿真预测的混响时间与实验测量的混响时间的误差均在10%以内,所得到的窗帘各倍频程的吸声系数即为最终预测值.
③ 建立有窗帘和课桌的教室仿真模型,对应现场测量实例④和⑤.抹灰层和窗帘的吸声系数采用步骤①和②的最终预测值,仅变化课桌各倍频程的吸声系数,使仿真预测的混响时间与实验测量的混响时间的误差均在10%以内,所得到的课桌各倍频程的吸声系数即为最终预测值.
各个实例的仿真分析过程中,模拟声线的数量均设置为2.0×104条,反射次数设置为200次,以保证混响时间的计算结果收敛.经过上述步骤后,校核后的教室3类吸声单元各倍频程(125~4 000 Hz)吸声系数的最终预测值如表2所示.
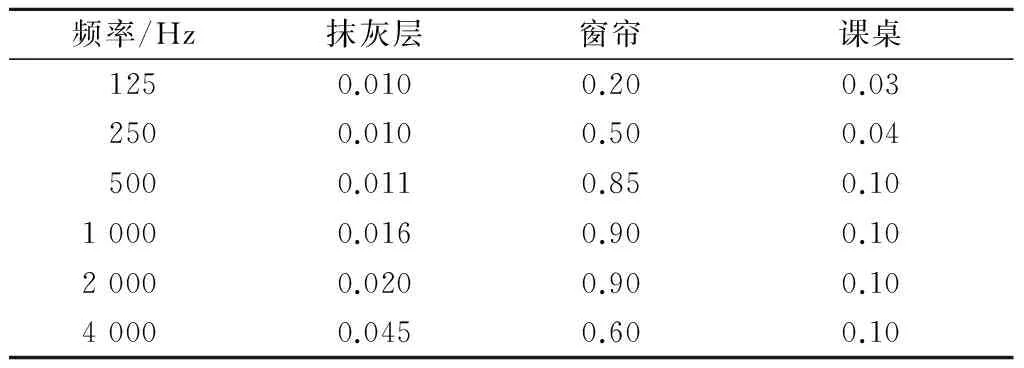
表2 仿真预测的3类吸声单元的倍频程吸声系数
利用最终校核完成的仿真模型分析得到的5个实例的教室中频混响时间与实际测量的中频混响时间的对比如表3所示.从表中可以得到:除实例②外,其他实例实验测量的中频混响时间和仿真模型预测值的吻合度均较好;实例③的相对误差最小,仅为0.98%;实例②的相对误差最大,达到8.41%.实例②和实例③的区别在于窗帘是否展开,当窗帘收起时预测结果误差增大,说明窗帘在展开和收起时其吸声系数存在一定的变化,即当窗帘收起时由于褶皱增加以及厚度增加,其吸声系数也随之变大,然而仿真模型中并未考虑此变化,导致误差产生.
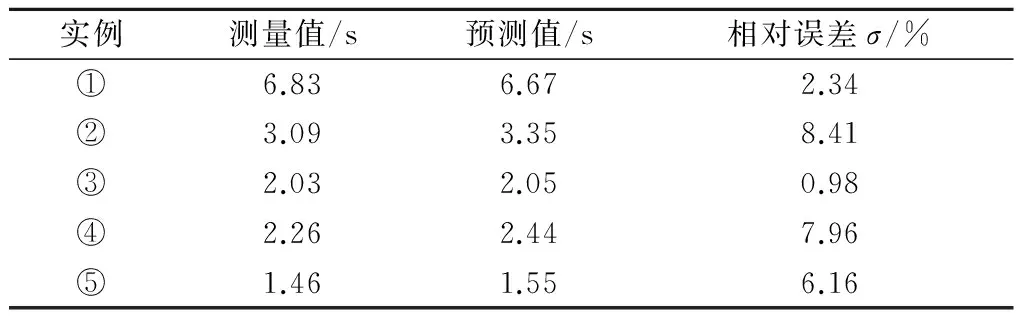
表3 教室中频混响时间的实验测量与仿真预测结果对比
3 结果讨论
本节将在已校核的仿真模型的基础上进一步分析窗帘和课桌的相关参数对教室混响时间的影响.2.2节已经说明窗帘的吸声系数受展开面积的影响,具有一定的不确定性.限于篇幅,本文暂不讨论窗帘吸声系数的这种不确定性变化,而仅讨论其展开面积变化对教室混响时间的影响.关于课桌则将讨论降噪系数(NRC,即250,500,1 000和2 000 Hz倍频程吸声系数的算术平均值)以及排列方式的变化对教室混响时间的影响.
3.1窗帘的展开面积对混响时间的影响
根据实验测量时获取的数据可知,该教室共有6幅窗帘,高度均为3 m,当窗帘均收起时总计展开面积10.7 m2,当窗帘全展开时总计展开面积48.6 m2.另外再增加窗帘展开面积分别为0,25和35 m2时的3种情况,讨论窗帘展开面积的变化对教室中频混响时间的影响.窗帘增加的总面积平均分配到6幅窗帘,仿真模型的参数设置保持不变,预测结果如图6所示.
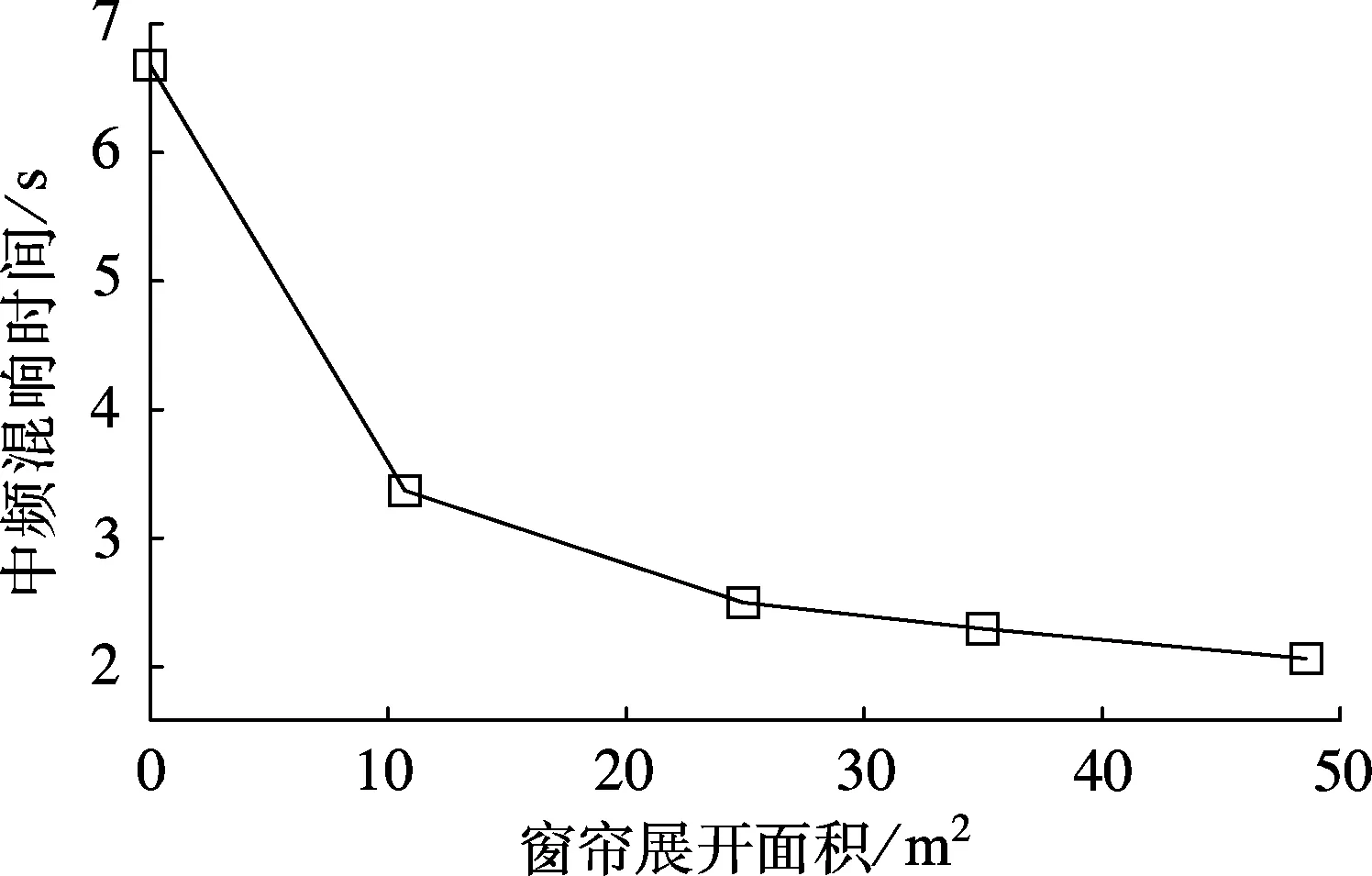
图6 不同窗帘展开面积时教室中频混响时间预测值
从图6可看到,窗帘展开面积分别为0(无窗帘),10.7(窗帘收起),25,35和48.6 m2(窗帘全展开)时,对应的教室中频混响时间分别为6.67,3.35,2.49,2.27, 2.05 s.窗帘存在与否对教室的中频混响时间的影响非常明显,例如当窗帘的展开面积为10.7 m2时,教室中频混响时间相对无窗帘的情况衰减了约50%.当窗帘存在时,其展开面积的逐渐变化对教室混响时间的影响则相对较小,且从图中曲线的变化趋势可以看到,当窗帘的展开面积较大时,再进一步增加面积所带来的混响时间衰减的效果越来越小.这是因为窗帘主要是通过其较高的吸声性能来改变教室混响,增加窗帘面积可使该吸声性能得到加强,但是窗帘的面积越大,吸声性能的强化越不明显.图6还表明,窗帘展开对教室空场混响时间的影响作用不可小视,当教室在具体使用中存在混响较大的情况时,尽可能拉开窗帘是一种简易且有效的方法.
3.2课桌NRC对混响时间的影响
由于常见简易课桌表面比较光滑,其吸声系数并不是很高,NRC为0.085,具有很大的提升空间.因此在此尝试讨论课桌NRC变化对教室混响时间的影响,考虑到实际常用座椅情况,课桌NRC上限设置为0.4,此外还设置了NRC分别为0,0.2和0.3(各倍频程频率的吸声系数等比例增加)的3种情况.仿真模型基于实例⑤,即教室存在课桌和呈全展开状态的窗帘,其他参数设置保持不变,所得到的教室中频混响时间的预测值如图7所示.
从图7可看到,课桌NRC分别为0,0.085,0.2,0.3和0.4时,对应的教室中频混响时间分别为1.83,1.55,1.30,1.17, 1.08 s.随着课桌NRC的增加,教室的中频混响时间有不断减小的趋势,同时课桌NRC越高,继续提高NRC对衰减教室混响时间的效果越来越差,这是因为课桌NRC的线性增加对整个教室内表面的等效平均吸声系数的贡献越来越低.当课桌存在且吸声系数为0时(此时课桌表面可视为声学刚性界面),教室的中频混响时间为1.83 s,对比实例③无课桌有窗帘全展开时的2.05 s,降低了0.22 s.结果表明,课桌降低教室混响时间的机理可能是由于以下2个方面:一是其表面的吸声,二是成片的课桌几何结构较明显地改变了教室的实际空间(成片桌面隔开了课桌上下的几何空间),一定程度上使教室有效的混响体积减小,进而使混响时间减小.这些推断还有待进一步研究验证.

图7 不同课桌NRC时教室中频混响时间预测值
3.3课桌排列方式对混响时间的影响
教室实际使用中,课桌的排列方式有可能变化,这对教室的空场混响时间可能造成影响.本节针对4种可能的课桌排列方式(见图8),对教室的空场混响时间分别进行了仿真分析.排列方式1为实验测量教室当前的课桌排列方式,4个座位一组共2列;排列方式2为2个座位一组共4列;排列方式3为8个座位一组共2列,且前后两个座位对向摆放;排列方式4为U型环绕式排列.所有排列方式中,课桌总数量保持不变,课桌表面NRC均为0.085,窗帘存在且均为全展开状态.仿真分析结果如图9所示,可以看到4种课桌排列方式对应的教室中频混响时间分别为1.55,1.61,1.57,1.51 s,相互之间的差值不超过0.1 s.该结果表明,在课桌数量与种类不变的情况下,课桌排列方式变化对教室中频混响时间的影响较小.

(a) 排列方式1 (b) 排列方式2

(c) 排列方式3 (d) 排列方式4
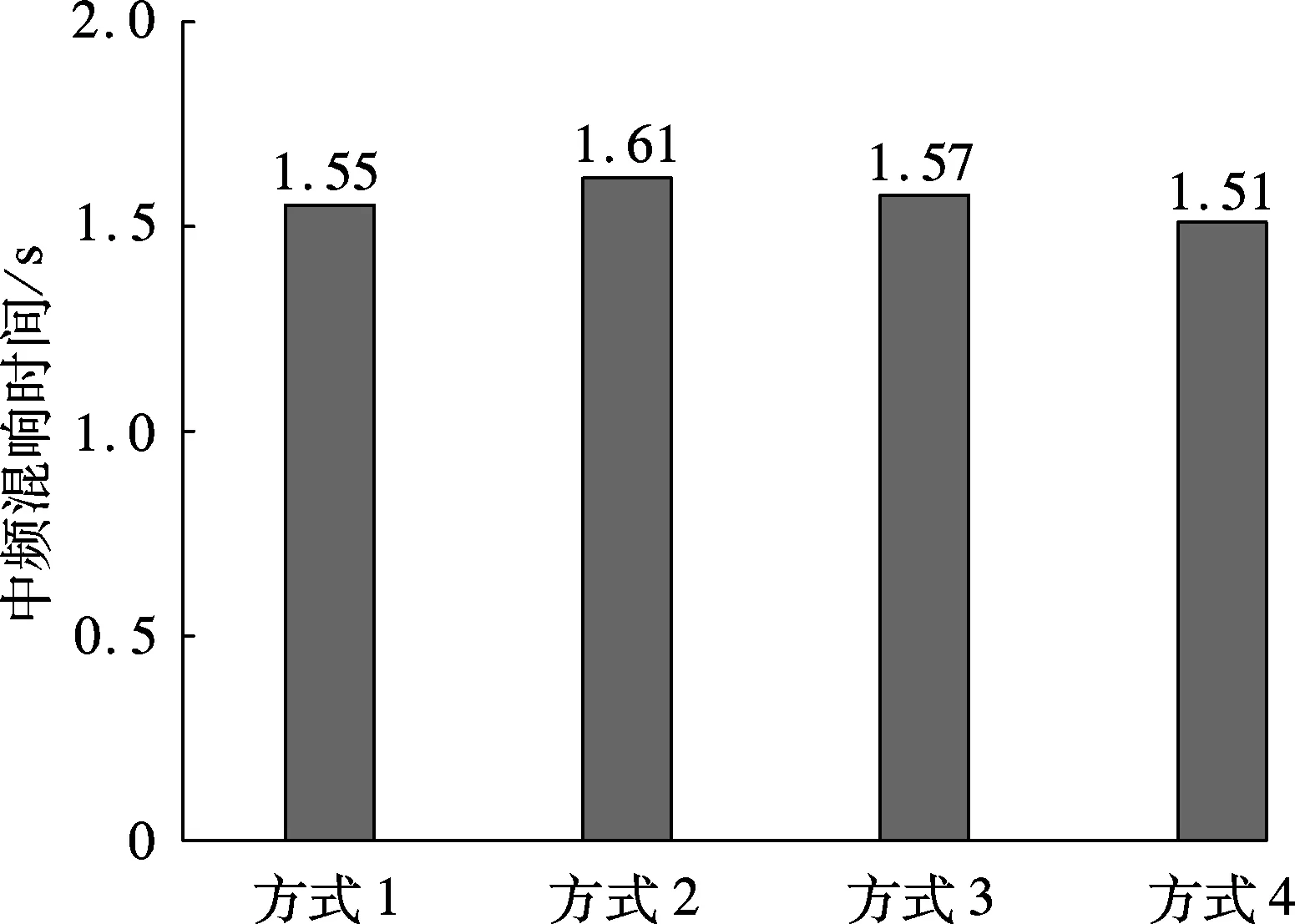
图9 4种课桌排列方式下的教室中频混响时间
4 结论
1) 国内大学教室中常见的简易布窗帘通过其较高的吸声性能,可使教室的空场混响时间降低54%以上.
2) 简易课桌通过其表面的吸声性能以及通过成片的几何结构来改变教室的有效混响体积,可使空场混响时间降低27%.
3) 课桌排列形式变化对教室的空场混响时间影响较小.
4) 在新建教室内装中,选择合适的窗帘与课桌,能明显改善教室混响时间至接近甚至满足国家标准建议值,是一种简便且高效的教室音质控制措施.该研究可对实际教室音质改善提供参考.
References)
[1]宋拥民, 盛胜我. 教室室内声学研究进展[J]. 声学技术, 2006, 25(1):56-61. DOI:10.3969/j.issn.1000-3630.2006.01.013.
Song Yongmin, Sheng Shengwo. Progress in classroom acoustics research[J].TechnicalAcoustics, 2006, 25(1):56-61. DOI:10.3969/j.issn.1000-3630.2006.01.013.(in Chinese)
[2]徐欢, 欧达毅. 教室声环境研究进展综述[J]. 建筑科学, 2015, 31(8):35-40. DOI:10.13614/j.cnki.11-1962/tu.2015.08.006.
Xu Huan, Ou Dayi. A review of classroom acoustics research and development[J].BuildingScience, 2015, 31(8):35-40. DOI:10.13614/j.cnki.11-1962/tu.2015.08.006.(in Chinese)
[3]Bradley J S. Predictors of speech intelligibility in rooms [J].JournaloftheAcousticalSocietyofAmerica, 1986, 80(3): 837-845.
[4]Hodgson M. Experimental investigation of the acoustical characteristics of university classrooms[J].JournaloftheAcousticalSocietyofAmerica, 1999, 106(4): 1810-1819. DOI:10.1121/1.427931.
[5]Hodgson M, Nosal E M. Effect of noise and occupancy on optimal reverberation times for speech intelligibility in classrooms [J].JournaloftheAcousticalSocietyofAmerica, 2002, 111(2): 931-939.
[6]宋拥民, 祝培生, 盛胜我. 教室室内最佳混响时间的研究[J]. 声学技术, 2009, 28(1): 48-52.
Song Yongmin, Zhu Peisheng, Sheng Shengwo. Research on optimal reverberation time in classrooms[J].TechnicalAcoustics, 2009, 28(1): 48-52.(in Chinese)
[7]中华人民共和国住房和城乡建设部. GB 50118—2010 民用建筑隔声设计规范[S]. 北京:中国建筑工业出版社,2010.
[8]Tang S K, Yeung M H. Reverberation times and speech transmission indices in classrooms[J].JournalofSoundandVibration, 2006, 294(3):596-607. DOI:10.1016/j.jsv.2005.11.027.
[9]李杰, 李浩, 张蓓. 普通教室混响时间的测量与分析[J]. 环境科学与管理, 2012, 37(12):122-125.DOI:10.3969/j.issn.1673-1212.2012.12.031.
Li Jie, Li Hao, Zhang Bei. Measurement and analysis of reverberation time in classrooms[J].EnvironmentalScienceandManagement, 2012, 37(12):122-125. DOI:10.3969/j.issn.1673-1212.2012.12.031.(in Chinese)
[10]Shield B, Conetta R, Dockrell J, et al. A survey of acoustic conditions and noise levels in secondary school classrooms in England[J].JournaloftheAcousticalSocietyofAmerica, 2015, 137(1): 177-188. DOI:10.1121/1.4904528.
[11]Peng J, Wang D, Lau S K, et al. An investigation of acoustic treatment for children in a classroom of an elementary school[J].AppliedAcoustics, 2015, 89: 42-45. DOI:10.1016/j.apacoust.2014.09.005.
[12]中华人民共和国住房和城乡建设部. GB/T 50076—2013 室内混响时间测量规范[S]. 北京:中国建筑工业出版社,2013.
[13]David A B, Colin H H.Engineeringnoisecontroltheoryandpractice[M]. 3rd ed. London: E& FN Spon Press, 2006: 314-332.
[14]Bistafa S R, Bradley J S. Predicting reverberation times in a simulated classroom[J].JournaloftheAcousticalSocietyofAmerica, 2000, 108(4): 1721-1731.
[15]Bistafa S R, Bradley J S. Predicting speech metrics in a simulated classroom with varied sound absorption[J].JournaloftheAcousticalSocietyofAmerica, 2001, 109(4): 1474-1482.
Influences of simple fabric curtains and desks on reverberation time in an unoccupied classroom
Guo Wencheng1,2Huang Gongjun3Min Hequn1,2
(1School of Architecture, Southeast University, Nanjing 210096, China)(2Key Laboratory of Urban and Architectural Heritage Conservation of Ministry of Education, Southeast University, Nanjing 210096, China)(3School of Civil Engineering, Southeast University, Nanjing 210096, China)
Influences of simple fabric curtains and desks on the reverberation time (RT) in an unoccupied university classroom were investigated experimentally and numerically. First, in-situ RT measurements were carried out by the interrupted noise method in a newly-built unoccupied classroom with a size of 16.8 m×10.2 m×3.78 m. Several conditions were considered: without curtains and desks, with curtains only, or with curtains and desks both. Secondly, acoustical simulation models of the classroom under the above conditions were built by Raynoise. Extensive comparisons were carried out between the simulated and measured results to obtain the absorption coefficients of the interior surface of the classroom, curtains and desks. The results show that, simple fabric curtain mainly depends on its high absorption, while the desk depends on its absorption and geometry structures to change the reverberation of the classroom, and the curtains and desks can reduce the reverberation time of the unoccupied classroom at least 54% and 27%, respectively.
classroom; sound absorption; reverberation time; noise control; acoustical comfort
10.3969/j.issn.1001-0505.2016.04.009
2016-01-24.作者简介: 郭文成(1990—),男,硕士生;闵鹤群(联系人),男,博士,副教授,hqmin@seu.edu.cn.
国家自然科学基金资助项目(51408113)、江苏省科技计划青年基金资助项目(BK20140623).
10.3969/j.issn.1001-0505.2016.04.009.
TU112
A
1001-0505(2016)04-0727-06
引用本文: 郭文成,黄功俊,闵鹤群.简易布窗帘及课桌对教室空场混响时间的影响[J].东南大学学报(自然科学版),2016,46(4):727-732.
