安培环路定理的正确应用*

张明铎　莫润阳　张引红　沈壮志

(陕西师范大学物理学与信息技术学院　陕西 西安　710119)



安培环路定理的正确应用*

张明铎莫润阳张引红沈壮志

(陕西师范大学物理学与信息技术学院陕西 西安710119)

安培环路定理是描述稳恒磁场性质的重要定理之一，它所描述的磁场分布与电流的关系适用于所有稳恒磁场．但是，只有对那些具有高度对称性分布的电流和磁场，应用安培环路定理分析磁场分布的数学过程才较为简便．

安培环路定理稳恒磁场磁感强度

1　引言

安培环路定理是描述稳恒磁场性质的重要定理之一，它反映了磁场的涡旋性及磁场分布与电流的关系，表明磁感应强度的环流不等于零．文献[1, 2]通过例证指出，文献[3～5]对安培环路定理的表述不准确．这一说法值得商榷．

2　安培环路定理的表述

文献[3～5]对安培环路定理的表述：在真空的稳恒磁场中，磁感强度B沿任一闭合路径的积分(即B的环流)的值等于μ0乘以该闭合回路所包围的各电流的代数和，即

(1)

文献[1, 2]认为这一表述不准确的例证如下：设有一有限长直电流，以该电流为轴做一圆形回路，如图1所示．按照上述定理闭合回路包围电流为I，则据式(1)得

(2)

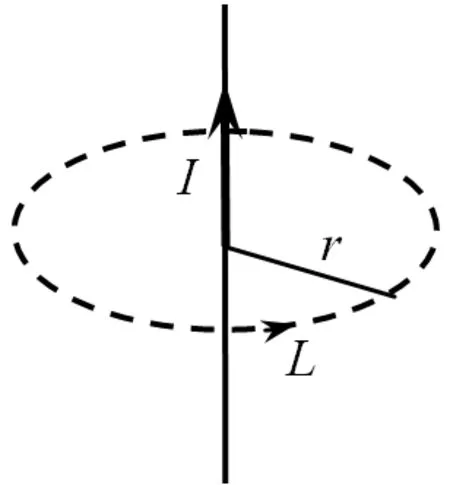
图1　有限长直电流磁场

这一结果显然是不对的，因为它反映的实际上是无限长直电流周围的磁场．

文献[1, 2]据此认为，安培环路定理应表述为：在真空的磁场中，磁感强度B沿任一闭合路径的积分(即B的环流)的值等于μ0乘以穿过以该闭合路径为围界的任意曲面所包围的各恒定电流的代数和，即

(3)

仔细分析不难看出，对安培环路定理的这两种描述其实是一样的，不同之处是对于“回路所包围的电流”的表述．文献[3～5]的叙述是“该闭合回路所包围的各电流的代数和”，文献[1, 2]叙述为“穿过以该闭合路径为围界的任意曲面所包围的各恒定电流的代数和”，其真实含义都是“穿过回路所包围区域的电流的代数和”．再者文献[1, 2]“以该闭合路径为围界的任意曲面所包围的各恒定电流的代数和”的说法值得商榷．顾名思义，“任意曲面”既可能是闭合曲面，也可能是非闭合曲面．只有对闭合曲面才有所谓“包围”的问题，而非闭合曲面则不然．

所以，本文认为文献[3～5]对安培环路定理的表述是不存在问题的，绝大多数大学物理教材正是这样表述的，而文献[1, 2]所述则远非准确．

3　用安培环路定理求解磁场分布应该注意的问题

根据安培环路定理，式(1)等号左边的磁感强度B是由回路内外所有电流(而非只是回路所包围电流)共同确定的；等号右边是B的环流，仅由回路所包围电流确定，即穿过回路包围区域的所有电流代数和的μ0倍．文献[1, 2]所举例证的不当之处在于对安培环路定理的错误理解和应用．

首先，形成稳恒电流的电路必然是闭合回路，所以独立的一段稳恒电流是不可能存在的．也就是说，图1所示直线电流实际上是某个闭合回路中的稳恒电流的一部分．

其次，图1所示闭合路径上任一点的磁感强度B实际上是由整个闭合电流共同产生的，而不是仅仅由图中的那一段直线电流产生．

再次，由于图中闭合路径上各点的磁感强度B是由整个闭合电流共同产生的，其方向就不一定总是沿着路径的切向，其大小也不一定处处相等．

那么如何利用安培环路定理来确定稳恒电流所激发的磁场呢？原则上说，该定理所描述的磁场分布与电流的关系适用于所有稳恒磁场．但是，并非任意电流都可以用该定理简便地求解其磁场分布，有些情况下甚至无法获得解析解．实际上，只有很少一部分稳恒电流的磁场能够用安培环路定理进行简便分析．

图2　无限长轴对称电流磁场

如图2所示无限长轴对称电流，这一模型可看作电流经由无限远处某点形成闭合．在垂直于对称轴的平面内做一圆形回路，圆心位于轴上，根据式(1)所述定理可得

(4)

只要求出相应回路所包围的电流∑Ii，即可确定距离轴线不同距离r处的磁感强度B的大小．

又如图3所示无限大均匀载流平面，假设在垂直于电流方向的单位宽度上电流强度为j．在与载流平面垂直的平面内做一矩形回路abcd，且ab，cd两条边与载流平面等距，根据式(1)所述定理可得

(5)

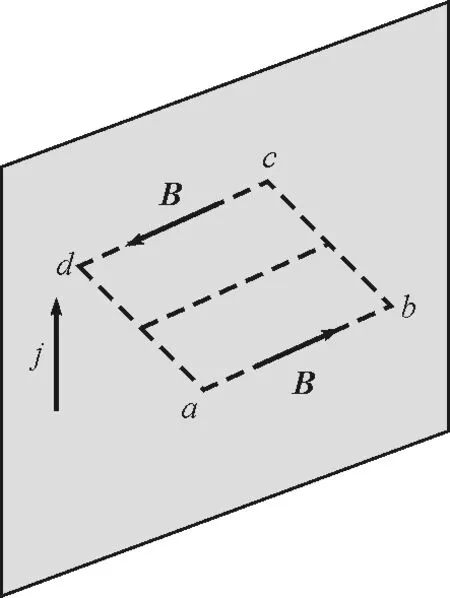
图3　有限长直电流磁场

对其他一些载流体，如密绕长直螺线管、密螺绕环等，也可采用类似的方法应用安培环路定理分析其磁场分布，这里不再赘述．

综上所述，只有对那些具有高度对称性分布(而非文献[1, 2]所说的某种对称性)的电流和磁场，应用安培环路定理分析磁场分布的数学过程才较为简便．结合对图2和图3的分析可知，应用安培环路定理求解稳恒电流所激发的磁场时，应该注意的主要问题有以下几点：

(1)分析电流和磁场的对称性．

(2)根据电流和磁场的对称性，选择适当形状的环路，求出∮LB·dl．这里所谓“适当形状的环路”的要求是

1)场点在环路上．

2)环路绕行方向要么垂直于B，要么与B平行．在与B垂直的路段B·dl=0；在与B平行的路段，还要求B的大小为常数，因而在相应路段有

这样即可简化积分运算，使数学处理过程简便．

4　结论

安培环路定理描述的磁场分布与电流的关系适用于所有稳恒磁场，只有准确理解其物理内涵，才能正确应用该定理简便地求解电流激发的磁场分布．这里的关键是分析电流和磁场的对称性，然后，根据电流和磁场的对称性，选择适当形状的环路求解磁感强度B的分布．

1张慧琨，张俊玲．安培环路定理的表述及其证明方法．山西师范大学学报(自然科学版)，2007，21(1)：69～71

2徐恩生，孙丽媛．稳恒磁场安培环路定理的论述与推导．沈阳航空工业学院学报，2005，22(4)：83～84

3张三慧．大学物理学·电磁学(第二版)．北京：清华大学出版社，1999.212～219

4王少杰，顾牧．新编基础物理学(下册)．北京：科学出版社，2011.71～77

5马文蔚．物理学．北京：高等教育出版社，2006.254～259

The Correct Application of Ampere Circuital Theorem

Zhang MingduoMo RunyangZhang YinhongShen Zhuangzhi

(College of Physics and Information Technology, Shaanxi Normal University,Xi’an,Shanxi710119)

Ampere circuital theorem is one of the important theorem describing the steady magnetic field. The relationship between the distribution of magnetic field and current it described are applicable to all the steady magnetic field. But, only for those with a highly symmetrical distribution of current and magnetic field, it was simple that the process of mathematics to analyze the magnetic field distribution by use of Ampere circuital theorem.

ampere circuital theorem;steady magnetic field;magnetic induction intensity

张明铎(1963-)，男，副研究员，主要从事声学与物理学领域的教学和科研工作.

2016-05-05)

*陕西师范大学2016年度校级综合教学改革研究项目，编号：16JG23