基于卢比变换码的分解重组编码算法

黄 胜，季瑞军，杨晓非

（重庆邮电大学光通信与网络技术重点实验室，重庆 400065）

基于卢比变换码的分解重组编码算法

黄 胜，季瑞军，杨晓非

（重庆邮电大学光通信与网络技术重点实验室，重庆 400065）

LT（卢比变换）码是第一个能够实际应用的数字喷泉码。尽管采用BP（置信）译码算法的LT码的编译码复杂度已接近线性，但依然会增加较大的时延。文章提出了一种DRE（分解重组编码）算法，对所有信息包分解后重新组合，分成多组并行编码，有效地降低了编码时间和译码的操作数，减少了数据传输时延。该编码方法可适用于不同度分布函数。仿真结果表明，当信息包数量K=1 000和2 000时，采用同样的度分布可以达到NRE（非重复编码）的性能，并能够减少约75%的编码时间和大量的译码操作数。

卢比变换码；置信译码；度分布

0　引 言

在现代通信网中，传统的纠错方法，例如自动重传请求，存在较大的缺点，需要增加一条额外的反馈信道，浪费了宝贵的信道资源，且会产生较大的时延，而前向纠错技术却不需要额外的信道。数字喷泉码是一种新型的前向纠删码，而LT（卢比变换）码是首个实际应用的数字喷泉码［1］，在卫星通信、移动通信和多媒体传输中都有深入的研究［2-3］。与经典的纠删码相比，LT码性能好，编译码复杂度接近线性，对于较大的数据也能以较小的代价进行纠错，节约了硬件成本，编译码的运算时间也大大减少，降低了传输时延。喷泉码无码率的特性使其能适应任何复杂的信道，例如卫星通信复杂多变的信道和广播通信的多路径传输等［4］。

本文对LT码的编码方法进行优化，将原始信息包分解重组后并行编码，缩短了进行编码的信息包长度，减少了编码时间。从二分图来看，编码包与信息包的连边因为参与编码的包长减少而缩减，通过降低边的数量及译码的消边操作间接减少了译码时间。仿真结果表明，相较于文献［5］的NRE（非重复编码）和原始LT码，同样开销下，采用文献［5］的度分布，DRE（分解重组编码）算法能够达到与其相似的译码成功率且产生的边数大量减少。

1　LT码编译码原理

1.1编码

LT码作为一种无码率的码字，可以在产生足够多的编码包后执行译码。假设信息包数量为K，编码过程为：在K个信息包中随机选择d个由其异或得到编码后的包，其中d为编码包的度，由度分布函数得到。编码中的重要部分是度分布，常见的度式中，d的范围是｛1，K｝；ρ（d）表示度数为d的概率，

（1）理想孤波分布

理想孤波分布假设每次译码迭代后都会有一个度为1的编码包产生，使得BP（置信）译码算法可以继续执行，初始化第一次译码有且只有1个度为1的编码包，剩下的编码包随着度数的增加，其占总编码包的比例依次减少：

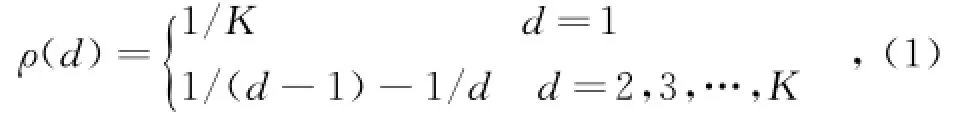
（2）RSD

Luby等人发现，在使用理想孤波分布时，译码后的效果并不理想，尤其是在信息包数量较小的情况下［1］。基数很小时，每次译码迭代后很难保证度1编码包一直存在，尤其是在译码初期的迭代过程中最容易造成译码中断。为了改善该问题，提出了RSD：分布有理想孤波分布和RSD（鲁棒孤波分布）［1］。

式中，

1.2译码

LT码采用的是BP译码算法，译码的开始需要一个度1编码包，通过不停迭代直到恢复完所有的信息包，具体步骤如下：

（1）从所有的编码包中查找度1的编码包是否存在，如果存在则转至步骤（2），不存在则译码失败；

（2）令度1编码包等于与其相连的信息包（即恢复出该信息包）；

（3）更新与此信息包相连的所有编码包，更新结果为它们的异或结果，更新后消除这些边；

（4）重复执行步骤（1）～（3）直至译码失败或信息包全部恢复。

图1所示为3个信息包和3个编码包时LT码的译码过程。图中，圆表示信息包，椭圆表示编码包，深色圆表示译码完成的信息包，深色椭圆表示选中的度1编码包。（a）～（c）对应步骤（1）～（3），（d）～（f）对应步骤（4），即重复前面3步迭代译码直到成功译码或失败。

图1　LT码的译码过程

2　分解重组编码策略

针对低传输时延的需求，本文基于LT码提出了一种DRE算法，以减少编码和译码的时间。DRE算法的主要步骤如下：

（1）对信息包分块，使每一块具有相等数量的编码包；

（2）对分块后的信息包重新组合，重组后的这组信息包长度不超过总的信息包的长度；

（3）按照步骤（2）分成多组信息包，使均等分的块在各组中出现的总次数相同；

（4）各组采用相同的度分布独立编码。

按照编码算法步骤进行分析，对于K个信息包，在编码时将它们n等分，每一份的数量用Ki表示：

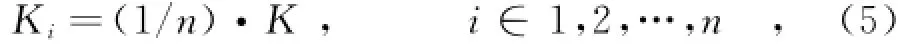
完成分块后，将各个块重新分成n-j组，其中j∈0，1，2，…，n-1，每组拥有n-P个块，其中P为降低每个分组的码块数量，P∈0，1，2，…，n-1。重新分组后进行编码，分组后的每组编码包长度为

编码后的信息包长被虚拟扩展，长度用K′表示：

可以由不同的度分布得到编码包的度数进行编码，由公式（2）～（6）得出每个分组的RSD为

为了达到只产生适当冗余的目的，每个分组产生的编码包数量必须要减少，数量控制为Ni，即

图2　DRE过程

图中，分块数n取4，标记为1～4。j=0，即分组数为4。P=1可以清楚地看到每个分组由3个块组成，且每个块在该分组中重复出现3次，即在编码过程中这些块重复参与3次，增加了编码包与信息包的相关性。编码可以采用任意度分布。

在分组时，如果分组后每组的块的数量小于总的块数，就可以达到降低译码时间的目的。图2所示的4个分组并行编码，这种情况下产生相同数量的编码包所需时间仅为普通编码的1/4。假如图2的分组只有3组，这样就无法均等处理每个分好的块，导致不等差错保护。为了避免这种情况发生，必须控制分组数和分块数的关系。由式（7）可以得知，需满足等式

经过DRE后，得到多组小于原信息包长的分组包，因此在编码时降低了编码包与信息包的边的数量。用e表示减少后的边的数量，由式（10）可知：

3　仿真分析

仿真参数如下：信息包数量K取1 000和2 000，信道模型为二进制删除信道，信道的删除概率P=0.1。LT码中度分布函数的参数为c=0.02，δ=0.2。仿真以开销和译码成功率来分析DRE算法的性能，开销ε可表示为ε=［（N-K）/K］·100。对比NRE算法和传统的LT码，对它们产生的边数进行比较。

图3所示为3种算法的译码成功率比较。DRE算法的取值与图2一致。仿真次数分别为1 000和2 000。由图可知，DRE算法可通过重组后并行编码，能节约大量的编码时间，在相同数量编码包的情况下可减少约75%的译码时间，而NRE算法和传统的LT码在编码时间上没有改变。

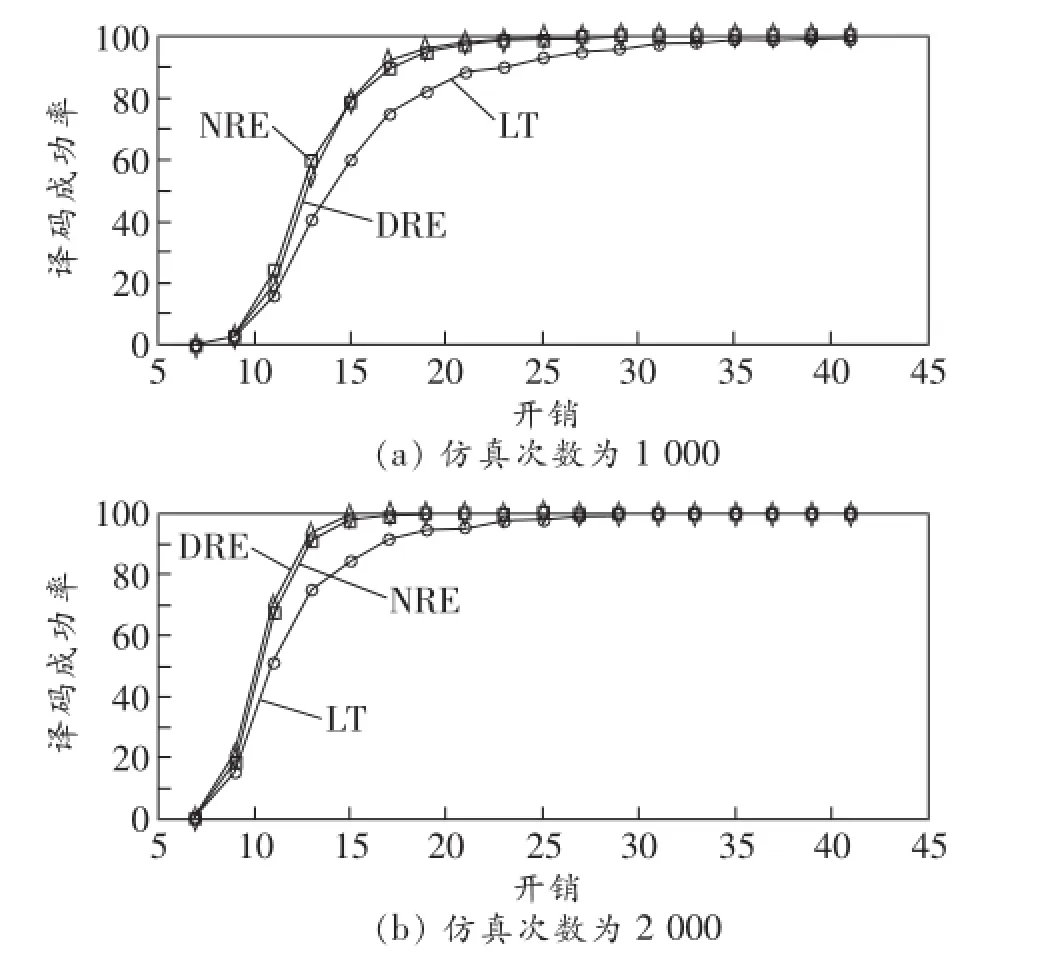
图3 3种算法的译码成功率比较

图4所示为仿真次数分别为1 000和2 000时3种算法的生成边数对比。可以看到生成边数随开销线性增长，这也侧面反映了BP译码算法的线性复杂度，且DRE算法能够有效地降低生成的边数。

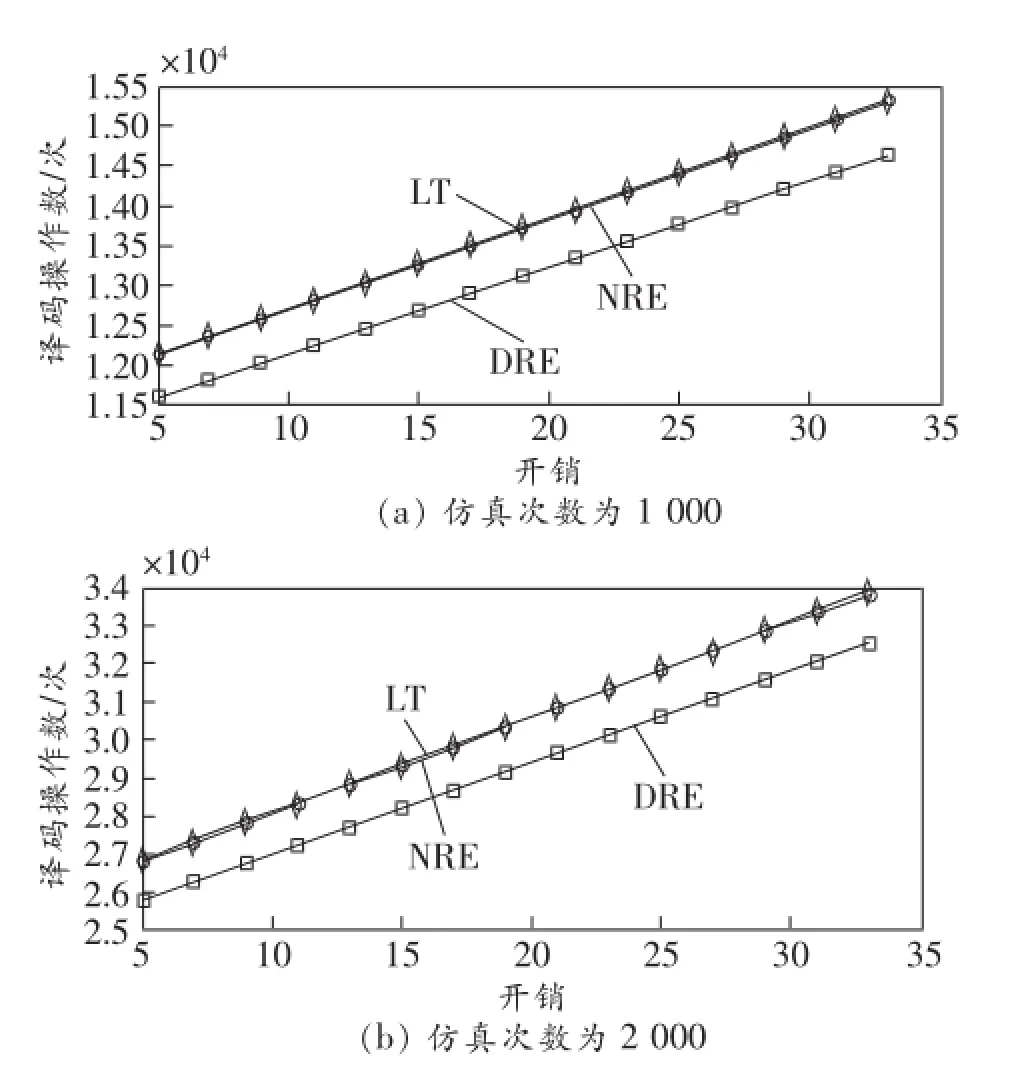
图4　3种算法的生成边数对比

4　结束语

本文提出了一种基于LT码的DRE算法，通过分解原始信息包并重新组合，多组并行编码，有效地降低了编码时间。分组后的信息包长度相对原始信息包有一定的缩减，使得编码包与信息包连边减少，因此减少了译码操作数并降低了译码时间。DRE算法与NRE算法和传统LT码算法相比，在同开销和度分布的情况下，有相似的译码成功率且能够有效降低传输时延。

［1］ Luby M.LT codes［C］//Foundations of Computer Science，2002.Vancouver，Canada：IEEE，2002：271-280.

［2］ Yao W D，Hui L I，Chen L J，et al.Study on the fountain codes technology in deep space communications［J］.Systems Engineering&Electronics，2009，31（1）：40-44.

［3］ Ahmad S，Hamzaoui R，Al-Akaidi M M.Unequal error protection using fountain codes with applications to video communication［J］.IEEE Trans Multimedia，2011，13（1）：92-101.

［4］ Wang N，Zhang Z.The impact of application layer Raptor FEC on the coverage of MBMS［C］//2008 IEEE Radio and Wireless Symposium.Orlando，FL，USA：IEEE，2008：223-226.

［5］ Yen K K，Liao Y C，Chen C L，et al.Non-Repetitive Encoding with Increased Degree-1 Encoding Symbols for LT Codes［C］//APCCAS 2012.Kaohsiung，China：IEEE，2012：655-658.

Decomposition and Restructuring Encoding Algorithm for LT Codes

HUANGSheng，JI Rui-jun，YANG Xiao-fei
（Key Laboratory of Optical Fiber Communication and Network Technology，Chongqing University of Posts and Telecommunications，Chongqing 400065，China）

LT codes are the first realization of the digital Fountain codes.LT codes using BP decoding algorithm which means the complexity is close to that of linear algorithm.However it still suffers from great delay.In order to solve this problem，we propose a decomposition and restructuring encoding algorithm.The algorithm first decomposes and regroups K information packets，and then divides the packets into a plurality of sets for parallel encoding.The algorithm can effectively reduce the encoding time and operation of decoding with reduced data transmission delay.The encoding method can be applied to various modifications distribution.In the case of K=1 000 and K=2 000 and the same degree distribution，the simulation results show that it can achieve Non-Repetitive Encoding（NRE）algorithm performance with 75%encoding time reduction and less decoding operands.

LT codes；BP decoding；degree distribution

TN911.22

A

1005-8788（2016）04-0012-04

10.13756/j.gtxyj.2016.04.004

2016-04-04

国家自然科学基金资助项目（61371096，61171158）；重庆市自然科学基金资助项目（cstc2013jcyj A40052）；重庆市教委科学技术研究项目（KJ130515）

黄胜（1974-），男，湖北英山人。教授，博士，主要研究方向为光互联网、未来网。

季瑞军，硕士研究生。E-mail：1120330180@qq.com