最小极大唯一哈密顿图存在2度点的证明
2016-09-20侯政
侯政
(无锡机电高等职业技术学校本科部,江苏无锡214028)
最小极大唯一哈密顿图存在2度点的证明
侯政
(无锡机电高等职业技术学校本科部,江苏无锡214028)
给出了最小极大唯一哈密顿图的定义和性质,研究了p( p≥3)阶最小极大唯一哈密顿图存在2度点的猜想,并利用辅助定理证明了p=8和p=10时,p( p≥3)阶最小极大唯一哈密顿图存在2度点。
哈密顿图;哈密顿圈;2度点
C.A.Barefoot等[1]首次提出了最小极大唯一哈密顿图的概念,同时提出了p( p≥3)阶最小极大唯一哈密顿图有2度点的猜想。A.D.Nhu等[2]对最小极大唯一哈密顿图做了研究,但并没能证明该猜想。在本文中,笔者也研究了该猜想,并证明了p=8和p=10时,p( p≥3)阶最小极大唯一哈密顿图存在2度点。
1 最小极大唯一哈密顿图及其性质
定义1:称p阶简单图G为最小极大唯一哈密顿图是指G满足以下条件:1)G中有且仅有一个哈密顿图;2)任加一条G中没有的线,能使G中哈密顿圈数增加;3)G中有最少的线。
C.A.Barefoot和R.C.Entringer证明了以下定理1。
定理1:设q(p)为p( p≥3)阶最小极大唯一哈密顿图的线数,则有以下结论成立:当3≤p≤7时,q( p)=2p−3,且p阶最小极大唯一哈密顿图是唯一的;当p≥8时,
在以下证明过程中,用G表示p( p≥8)阶最小极大唯一哈密顿图,C表示G中仅有的哈密顿图。用分别表示G中的点x、y在子图S中相邻、不相邻。
定义2[3]:设,若存在vs、vt,且使得vs和vt相邻,vs+1和vt+1不相邻,则称G中存在θ-邻接。
显然,p( p≥8)阶最小极大唯一哈密顿图中不存在θ-邻接。
定理2[4]:在阶数至少为3的多重图H中,若除u、v外的所有点的度均为奇数,则H中有偶数(可能为零)条哈密顿路联结u和v。
定理2也称为Thomason定理。
2 辅助定理及其证明
根据以上定义和定理,可以得到下面几个辅助定理。
定理3:若δ(G)>2,则有以下结论成立:1)δ(G)=3,∆(G)=4;2)当p为偶数时,G中有且仅有两个度为4的点u和v,且u和v不相邻;3)p为奇数时,G中有且仅有三个度为4的点u、v和w,且这些点在子图G-C中独立。
根据以上推导,有
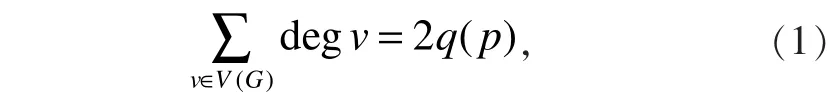
且有:当p为偶数时,2q(p)的值为3p+2;当p为奇数时,2q(p)的值为3p+3。
综上所述,有
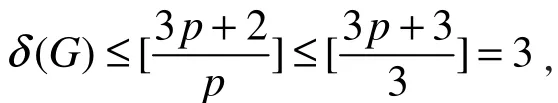
又由于δ(G)>2,因此有δ(G)=3。
由(1)式可得如下结论:当p为偶数时,δ(G)≤∆(G)≤δ(G)+2=5;当p为奇数时,δ(G)≤∆(G) ≤δ(G)+3=6。在以上推导中,有∆(G)≠5。若∆(G)=5,则G中至多有一个点u的度为偶数。若令v∈V( G),且有uadjv ,则u和v间有一条哈密顿路,于是由定理2
C可知u和v间至少有两条哈密顿路,从而可知G中至少有一个不同于C的哈密顿圈[5],这与G的唯一性矛盾,故有∆(G)≠5。同理可证,∆(G)≠6。综上所述,可知∆(G)=4。
2)由式(1)及∆(G)=4可知,当p为偶数时,G中有且仅有两个度为4的点u和v。
下面用反证法证明u和v不相邻。
假设u和v相邻,则存在以下两种情形。
无论以上哪一种情况,p为偶数时,G中有且仅有两个度为4的点u和v,且u和v是不相邻的。
3)由式(1)和∆(G)=4可得,p为奇数时,G中有且仅有三个度为4的点u、v和w。
下面用反证法证明u、v和w在子图G-C中独立。
定理4:当p为偶数,且δ(G)>2时,有以下结论成立:1)N( u)∩N( v)中至多有一个点x,若这样的x存在,x和u及x和v则在子图C中相邻;2)对任意的y∈N( u),且,对任意的z∈N( v),且,则有y和z不相邻。其中:u和v为G中仅有的两个4度点,N(u)和N(v)分别表示u和v的邻域。
证明:1)若存在y∈V( G),且y∈N( u)∩N( v ),则存在以下三种情形:
对于情形1,可以得出与deg y=3矛盾的结论。
对于情形2,由定理2可知,G-yv中至少有两条哈密顿路[6]联结y和u,由此可得G中至少存在一不同于C的哈密顿圈,这与G的唯一性矛盾。
综合以上证明过程,情形1和情形2可以排除,由此可知情形3是成立的。由于p≥8,故N( u)∩N( v)中至多有一个点x。
2)若y和z相邻,则需要分成两种情形讨论。
3 主要结论
定理5:在p=8或p=10时,最小极大哈密顿图G 有2度点。
证明:设u、v∈V( G),及degu=degv=4,下面用反证法证明定理5。
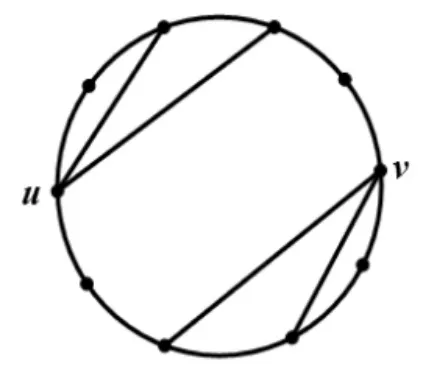
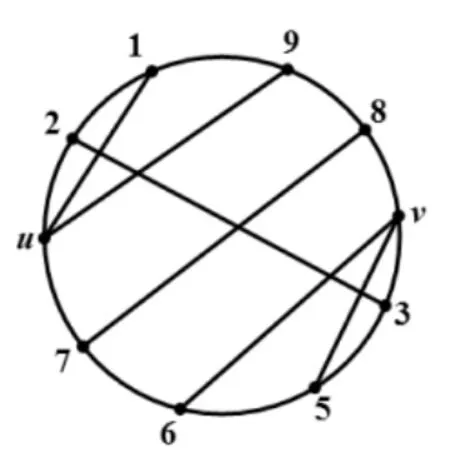
1)若p=8时结论不成立,可设C=v0v1…v7v0, v0=u,且,其中i 2)若p=10时结论不成立,则由定理3和定理4可知,G中所有点在C上的分布情况只能有以下两种情形:情形1是存在x∈V( G),且有。此时的N(u)和N(v)如图1所示,由图1可以看出,x与u、v相邻。情形2是N( u)∩N( v)=∅。此时N(u)和N(v)只能如图2所示,这样的x是不存在的。 图1 x与u、v相邻的情形 图2 x不存在的情形 对于以上两种情形,各点的邻接情况可以描述为以下三种类型。 图1(a)中各点的邻接关系只能表示为图3的形式,但该图中有一个不同于C的哈密顿圈 图1(b)中各点的邻接关系只能表示为图4的形式,但该图中有一个不同于C的哈密顿圈 图2中各点的邻接关系只能表示为图5的形式,但该图中也有一个不同于C的哈密顿圈 由以上证明过程可知,无论G中所有点的邻接情况如何,G中总存在一个与C不相同的哈密顿圈C′,这与G的唯一性相矛盾,因此G中必有2度点。 图3 邻接关系1 图4 邻接关系2 图5 邻接关系3 在本文中,笔者证明了p=8和p=10时,p( p≥3)阶最小极大唯一哈密顿图存在2度点,但没有证明p取其他值的情形,这也是需要进一步研究的问题。 [1]BAREFOOT C A,ENTRIGER R C.Extremal Maximal Uniquely Hamiltonian Graphs[J].Journal of Graph Theory,1980,4(1):93-100. [2]NHU AD,DINH H V.Necessary and Sufficient Condition for Maximal Uniquely Hamiltonian Graphs[J]. International Journal of Advanced Research in Computer Science,2012,3(5):114-116. [3]THOMASON A G.Hamiltonian Cycles and Uniquely Edge Colourable Graphs[J].Annals of Discrete Mathematics,1978,3:259-268. [4]李修睦.图论导引[M].武汉:华中工学院出版社,1982:203-244. [5]周秀君.一类独立数为4图的结构研究[J].长江大学学报(自然科学版),2011(3):1-3. [6]HARARY F.图论[M].李慰萱,译.上海:上海科学技术出版社,2008:75-98. [7]张先迪,李正良.图论及其应用[M].北京:高等教育出版社,2005:78-89. 【责任编辑王云鹏】 Proof of the Existence of a 2-degree Vertex for the Minimum Maximal Unique Hamilton Graph HOU Zheng The definition and properties of the minimal maximal unique Hamilton graph were given in this paper.The conjecture of the existence of 2-degree vertex for the minimum maximal unique Hamilton graph was studied.According to the auxiliary theorem,there was a proof thatp( p≥3)order of the minimum maximal unique Hamilton graph had a 2-degree vertex,when p was equal to 8 and 10. Hamilton graph;Hamilton cycle;2-degree vertex O157.5 A 2095-7726(2016)03-0010-03 2015-12-31 侯政(1976-),男,江苏无锡人,讲师,硕士,研究方向:图论、概率统计和数学教学。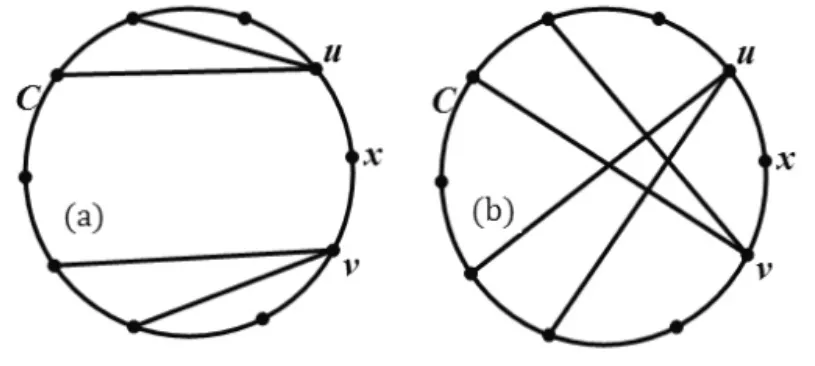
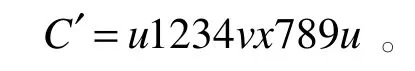
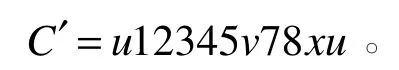

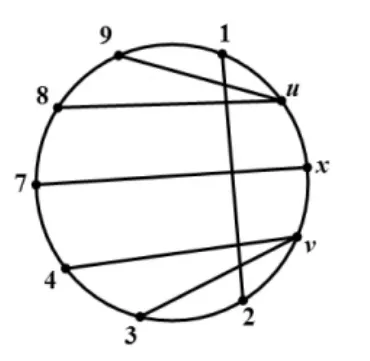
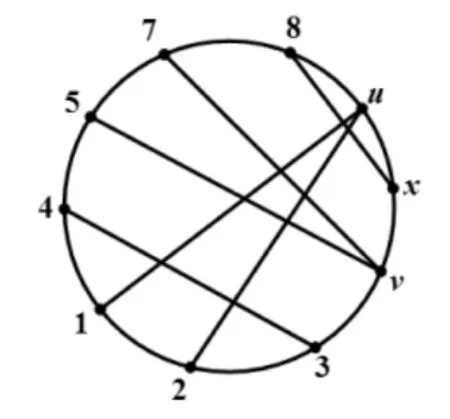
4 结束语
(Department of Undergraduate,Wuxi Electromechanical Higher Vocational and Technical School,Wuxi 214028,China)
